Динамические структуры данных: очередь и стек
Очереди
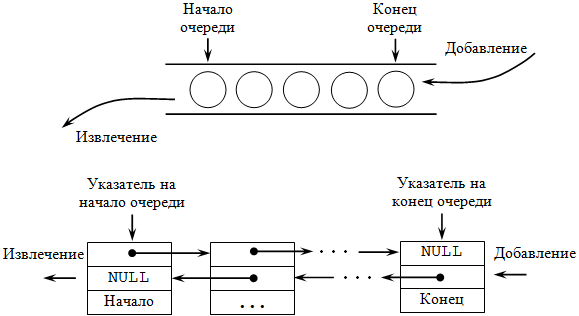
Очередь – это структура данных, представляющая собой последовательность элементов, образованная в порядке их поступления. Каждый новый элемент размещается в конце очереди; элемент, стоящий в начале очереди, выбирается из нее первым. В очереди используется принцип доступа к элементам FIFO ( First Input – First Output, "первый пришёл – первый вышел") ( рис. 30.2). В очереди доступны два элемента (две позиции): начало очереди и конец очереди. Поместить элемент можно только в конец очереди, а взять элемент только из ее начала. Примером может служить обыкновенная очередь в магазине.
Описание очереди выглядит следующим образом:
struct имя_типа {
информационное поле;
адресное поле1;
адресное поле2;
};где информационное поле – это поле любого, ранее объявленного или стандартного, типа;
адресное поле1, адресное поле2 – это указатели на объекты того же типа, что и определяемая структура, в них записываются адреса первого и следующего элементов очереди.
Например:
1 способ: адресное поле ссылается на объявляемую структуру.
struct list2 {
type pole1;
list2 *pole1, *pole2;
}2 способ: адресное поле ссылается на ранее объявленную структуру.
struct list1 {
type pole1;
list1 *pole2;
}
struct ch3 {
list1 *beg, *next ;
}Очередь как динамическую структуру данных легко организовать на основе линейного списка. Поскольку работа идет с обоими концами очереди, то предпочтительно будет использовать линейный двунаправленный список. Хотя для работы с таким списком достаточно иметь один указатель на любой элемент списка, здесь целесообразно хранить два указателя – один на начало списка (откуда извлекаем элементы) и один на конец списка (куда добавляем элементы). Если очередь пуста, то списка не существует, и указатели принимают значение NULL.
Описание элементов очереди аналогично описанию элементов линейного двунаправленного списка. Поэтому объявим очередь через объявление линейного двунаправленного списка:
struct Queue {
Double_List *Begin;//начало очереди
Double_List *End; //конец очереди
};
. . . . . . . . . .
Queue *My_Queue;//указатель на очередьОсновные операции, производимые с очередью:
- создание очереди;
- печать (просмотр) очереди;
- добавление элемента в конец очереди;
- извлечение элемента из начала очереди;
- проверка пустоты очереди;
- очистка очереди.
Реализацию этих операций приведем в виде соответствующих функций, которые, в свою очередь, используют функции операций с линейным двунаправленным списком.
//создание очереди
void Make_Queue(int n, Queue* End_Queue){
Make_Double_List(n,&(End_Queue->Begin),NULL);
Double_List *ptr; //вспомогательный указатель
ptr = End_Queue->Begin;
while (ptr->Next != NULL)
ptr = ptr->Next;
End_Queue->End = ptr;
}
//печать очереди
void Print_Queue(Queue* Begin_Queue){
Print_Double_List(Begin_Queue->Begin);
}
//добавление элемента в конец очереди
void Add_Item_Queue(int NewElem, Queue* End_Queue){
End_Queue->End = Insert_Item_Double_List(End_Queue->End,
0, NewElem)->Next;
}
//извлечение элемента из начала очереди
int Extract_Item_Queue(Queue* Begin_Queue){
int NewElem = NULL;
if (Begin_Queue->Begin != NULL) {
NewElem = Begin_Queue->Begin->Data;
Begin_Queue->Begin=Delete_Item_Double_List(Begin_Queue->Begin,0);
//удаляем вершину
}
return NewElem;
}
//проверка пустоты очереди
bool Empty_Queue(Queue* Begin_Queue){
return Empty_Double_List(Begin_Queue->Begin);
}
//очистка очереди
void Clear_Queue(Queue* Begin_Queue){
return Delete_Double_List(Begin_Queue->Begin);
}Пример 2. Дана последовательность ненулевых целых чисел. Признаком конца последовательности является число 0. Найдите среди них первый наибольший отрицательный элемент. Если такого элемента нет, то выведите сообщение об этом.
В данной задаче будем использовать основные операции для работы с очередью, рассмотренные ранее. Приведем главную функцию и функцию для реализации поиска первого наибольшего отрицательного элемента.
//главная функция
int _tmain(int argc, _TCHAR* argv[]){
int n;
Queue *My_Queue;
My_Queue = new Queue();
Make_Queue(1,My_Queue);
while (My_Queue->End->Data != 0){
cout << "Введите значение ";
cin >> n;
Add_Item_Queue(n,My_Queue);
}
cout << "\nОчередь: \n";
Print_Queue(My_Queue);
Find_Max_Negative_Element(My_Queue);
system("pause");
return 0;
}
//функция поиска первого наибольшего отрицательного элемента
void Find_Max_Negative_Element(Queue* Begin_Queue){
int tmp;
int max=Extract_Item_Queue(Begin_Queue);
while (Begin_Queue->Begin->Data != 0) {
tmp = Extract_Item_Queue(Begin_Queue);
if (max > 0 || tmp < 0 && abs(tmp) < abs(max))
max = tmp;
}
if (max > 0) printf("Элементов нет!");
else printf("Есть такой элемент: %d", max);
}Ключевые термины
FIFO (First Input – First Output) – это метод доступа к элементам очереди по принципу , "первый пришёл – первый вышел".
LIFO (Last Input – First Output) – это метод доступа к элементам стека по принципу "последним пришел – первым вышел"
Вершина стека – это доступный элемент стека.
Конец очереди – это позиция доступного для вставки в очередь элемента.
Начало очереди – это позиция доступного для извлечения из очереди элемента.
Очередь – это структура данных, представляющая собой последовательность элементов, образованная в порядке их поступления.
Стек – это структура данных, в которой новый элемент всегда записывается в ее начало (вершину) и очередной читаемый элемент также всегда выбирается из ее начала.
Краткие итоги
- Стек и очередь – это частные случаи линейного списка.
- Стек является списком, у которого доступен один элемент, называемый вершиной стека. Поместить или извлечь элемент можно только из вершины списка.
- Стек и очередь как динамические структуры данных можно организовать на основе линейного списка.
- Основными операциями со стеком являются: создание стека; печать (просмотр) стека; добавление элемента в вершину стека; извлечение элемента из вершины стека; проверка пустоты стека; удаление стека.
- Очередь является списком, у которого доступны два элемента: начало и конец очереди. Поместить элемент можно только в конец очереди, а взять элемент только из ее начала.
- Основными операциями с очередью являются: создание очереди; печать (просмотр) очереди; добавление элемента в конец очереди; извлечение элемента из начала очереди; проверка пустоты очереди; удаление очереди.
- Стек и очередь более экономно расходуют адресное пространство по сравнению с однонаправленными и двунаправленными списками.