Алгоритм перебора с возвратом

Цель лекции: изучить рекурсивный алгоритм перебора с возвратом, научиться разрабатывать рекурсивную триаду и алгоритм перебора с возвратом при решении задач на языке C++.

Во многих практических задачах из различных предметных областей требуется найти общее количество вариантов решения, число элементов в полном наборе решений. Иногда, исходя из постановки задачи, достаточно найти один из вариантов, соответствующих условию задачи. В некоторых задачах изучается вопрос о существовании решения как такового.

Ответы на поставленные вопросы, как правило, требуют проведения исчерпывающего поиска в некотором множестве всех возможных вариантов, среди которых находятся решения конкретной задачи. Существуют два общих метода организации исчерпывающего поиска: перебор с возвратом (backtracking) и его естественное логическое дополнение - метод решета.

Решение задачи методом перебора с возвратом строится конструктивно последовательным расширением частичного решения. Если на конкретном шаге такое расширение провести не удается, то происходит возврат к более короткому частичному решению, и попытки его расширить продолжаются. Для ускорения перебора с возвратом вычисления всегда стараются организовать так, чтобы была возможность отказаться как можно раньше от как можно большего числа заведомо неподходящих вариантов. Незначительные модификации метода перебора с возвратом, связанные с представлением данных или особенностями реализации, имеют и иные названия: метод ветвей и границ (branch and bound), поиск в глубину (depth first search), метод проб и ошибок и т. д. Перебор с возвратом практически одновременно и независимо был изобретен многими исследователями еще до его формального описания. Он находит применение при решении различных комбинаторных задач в области искусственного интеллекта.

При использовании метода решета вместо конструктивного построения решений задачи из множества возможных вариантов исключаются все элементы, не являющиеся решениями. Методы решета нашли широкое применение в теоретико-числовых задачах.

Метод перебора с возвратом и метод решета, строго говоря, не являются ни методами, ни алгоритмами решения задач. Их следует воспринимать как на некоторые общие схемы, которые применяются для решения той или иной задачи. Реализация этих схем в виде конкретных алгоритмов часто требует значительных дополнительных усилий в представлении данных и описании зависимостей между ними.

Соединение метода перебора с возвратом и рекурсии определяет специфический способ реализации рекурсивных вычислений и называется возвратной рекурсией. Это соединение двух эффективных методов реализации переборных алгоритмов.

При использовании возвратной рекурсии отпадает необходимость непосредственно организовывать возвраты и отслеживать правильность их осуществления. Они, как правило, становятся встроенной частью механизма выполнения рекурсивных вызовов.

Вычислительная схема перебора с возвратом

Опишем общую постановку класса задач, к которым заведомо применим алгоритм перебора с возвратом.

Пусть M₀, M₁, ...,M_n-1 - n конечных линейно упорядоченных множеств и G - совокупность ограничений (условий), ставящих в соответствие векторам вида 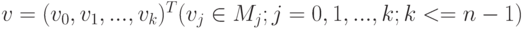, булево значение { истина,ложь } . Векторы v=(v₀,v₁,...,v_k)^T, для которых G(v) = истина, назовем частичными решениями. Пусть, далее, существует конкретное правило P, в соответствии с которым некоторые из частичных решений могут объявляться полными решениями. Тогда возможна постановка следующих поисковых задач.

• Найти все полные решения или установить отсутствие таковых.
• Найти хотя бы одно полное решение или установить его отсутствие.

Общий метод решения приведенных задач состоит в последовательном покомпонентном наращивании вектора v слева направо, начиная с v₀, и последующих проверках его ограничениями G и правилом P.

В общем случае этот метод приводит к алгоритмам с экспоненциальной временной сложностью, а применяется он в основном к классу так называемых Np -полных задач (задача коммивояжера, задача о рюкзаке и т. д.). Задачи этого класса эквивалентны друг другу в том смысле, что все они разрешимы недетерминированными алгоритмами полиномиальной сложности. Для них известно, что либо все они разрешимы, либо ни одна из них не разрешима детерминированными алгоритмами полиномиальной сложности. Иными словами, если хотя бы для одной из этих задач не существует детерминированного алгоритма, имеющего в худшем случае полиномиальную трудоемкость, то такие алгоритмы не должны существовать и для остальных задач этого класса. Наоборот, если хотя бы для одной из этих задач удалось найти детерминированный алгоритм, имеющий в худшем случае полиномиальную трудоемкость, то подобные алгоритмы существовали бы и для остальных задач этого класса и, более того, их можно было бы построить.

Опишем схему выполнения недетерминированного алгоритма. Пусть алгоритм выполняется до тех пор, пока не доходит до места, с которого должен быть сделан выбор из нескольких альтернатив. Детерминированный алгоритм однозначно осуществит выбор конкретной альтернативы и продолжит работать в соответствии с эти выбором. Недетерминированный алгоритм исследует все возможности одновременно, как бы копируя себя для реализации вычислений по всем альтернативам одновременно. Далее все копии работают независимо друг от друга и по мере необходимости продолжают создавать новые копии. Копия, сделавшая неправильный или безрезультатный выбор прекращает свою работу. Копия, нашедшая решение задачи, объявляет об этом, давая тем самым сигнал другим копиям о прекращении вычислений. Недетерминированные алгоритмы, являясь весьма полезной и продуктивной абстракцией, рекурсивны по сути, ибо при реализации оператора выбора фактически обращаются сами к себе.

Возможно, что многие задачи, решаемые методом перебора с возвратом, могут быть решены более эффективно другими способами. Однако ценность метода перебора с возвратом в соединении с рекурсией неоспорима. Во-первых, программы решения многих задач строятся по единой схеме, а во-вторых, они компактны и тем самым просты для понимания и усвоения соответствующих идей.

Пример 1. Задача о расстановке ферзей на шахматной доске.

Составьте рекурсивную функцию, находящую возможную расстановку n ферзей на шахматной доске размером nxn так, чтобы они не били друг друга ( n – натуральное число).

В соответствии с общей схемой алгоритма перебора с возвратом предложенную задачу можно решать по алгоритму "Все расстановки", но завершить выполнение алгоритма при нахождении первой требуемой расстановки или при получении вывода о невозможности получить нужную комбинацию. Согласно алгоритму ферзи расставляются последовательно на вертикалях с номерами от нуля и далее. В процессе выполнения предписания возможны снятия ферзей с доски (возвраты).

Алгоритм "Все расстановки"

Шаг 1. Полагаем 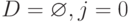( D - множество решений, j - текущий столбец для очередного ферзя).

Шаг 2. Пытаемся в столбце j продвинуть вниз по вертикали или новый (если столбец j пустой), или уже имеющийся там ферзь на ближайшую допустимую строку. Если это сделать не удалось, то переходим к шагу 4.

Шаг 3. Увеличиваем j на 1, то есть переходим к следующему столбцу. Если j<n-1, то переходим к шагу 2. В противном случае j=n-1, то есть все вертикали уже заняты. Найденное частичное решение запоминаем в множестве D и переходим к шагу 2.

Шаг 4. Уменьшаем j на 1, то есть снимаем ферзь со столбца j и переходим к предыдущему столбцу. Если j>0, то выполняем шаг 2. Иначе вычисления прекращаем. Решения задачи находятся в множестве D, которое, может быть и пустым.

Решение задачи для небольших размеров доски можно найти "вручную", но для разработки алгоритма необходимо провести моделирование условия и остановиться на каком-либо представлении данных.

Проведем параметризацию задачи. Введем четыре вспомогательных вектора: pos, ho, dd и du c длинами n, n, 2n-1 и 2n-1 соответственно. Использовать их будем следующим образом ( рис. 36.1):

• ho_i=1, если на горизонтали с номером i (i=0,1,...n-1) имеется ферзь, и ho_i=0 - в противном случае;
• du_s=1, если на диагонали с номером s (s=0,1,...2n-2), идущей слева направо и снизу вверх, имеется ферзь, и du_s=0 - в противном случае;
• dd_s=1, если на диагонали с номером s (s=0,1,...2n-1), идущей слева направо и сверху вниз, имеется ферзь, и dd_s+1=0 - в противном случае;
• pos_j=i, если в позиции (i,j) (i,j=0,1,...n-1) стоит ферзь.

Рис. 36.1. Схема использования вспомогательных массивов в задаче

Использование этих соглашений позволяет получить такие утверждения:

• В позицию (i,j) можно поставить ферзь, если ho_i+du_i+j+dd_n+i-j=0.
• Поставить ферзь в позицию (i,j) равносильно присваиваниям: ho_i=1, du_i+j=1, dd_n+i-j=1.
• Убрать ферзь из позиции (i,j) равносильно присваиваниям: ho_i=0, du_i+j=0, dd_n+i-j=0.

Данное описание алгоритма является моделью решения общей задачи о нахождении всех вариантов расстановок. Рекурсия здесь осуществляется по не совсем стандартной схеме. В каждом рекурсивном вызове глубины j делается попытка поместить ферзь в некоторую позицию i столбца j (i,j=0,1,...n-1), а сам вызов соответствует переходу от работы с текущим столбцом к работе со следующим столбцом. При этом в начале вычислений и при переходах к любому последующему рекурсивному вызову параметр i меняется от нуля и далее с шагом, равным единице, пытаясь принять значение наименьшего номера поля, допустимого для установки ферзя. При переходах к любому предыдущему рекурсивному вызову параметр i продолжает изменяться от своего текущего на данном уровне значения с шагом, равным единице, также пытаясь принять значение наименьшего номера поля, допустимого для установки ферзя. Если в текущем столбце ферзь установить уже не удается, то создавшуюся ситуацию назовем тупиком. Попадание в тупик приводит к завершению текущего рекурсивного вызова, то есть к возврату к предыдущему столбцу и продолжению работы с ним. Иных случаев завершения рекурсивных вызовов не существует. Поэтому базой рекурсии мы должны считать совокупность всех тупиков. Заметим, что в данном случае элементы базы заранее до вычислений неизвестны.

После установки ферзя в одну из строк i последнего столбца i=n-1 формируется одно из решений задачи – при поиске одного варианта расстановки на этом этапе следует завершить выполнение алгоритма. При поиске всех расстановок вычисления прекращаются, когда мы попадаем в тупик при работе со столбцом 0. Полученные решения задачи, если они есть, возвращаются в виде столбцов матрицы otv, начиная от первого и далее.

Рассмотрим, как реализуется декомпозиция. Для этого вместо исходной задачи удобно решать ее следующее обобщение.

На доске размера nxm (m=n,n-1,...,0) требуется установить m ферзей так, чтобы они не били друг друга. При этом имеются некоторые клетки доски, на которые ферзь заведомо ставить нельзя. Множество этих "запретных" клеток обозначим через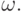

Исходная задача есть 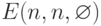. Проведем ее декомпозицию. Представим доску в виде двух частей: нулевого столбца (A) и оставшейся части (B). Соответственно этому разбиению будем решать задач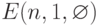и и . Каждое из n возможных решений i (ферзь установлен в строке i=0,1,...n-1 ) первой задачи однозначно определяет множество 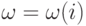запретных клеток для второй задачи. При этом в 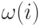попадают те клетки B, которые в "объединенной" доске бьет ферзь, установленный в строке i доски A. Пусть i зафиксировано и найдено множество d(i) решений второй задачи для доски B. Тогда расположение ферзя в строке i доски A и любое из полученных решений на B в совокупности дают различные решения otv(i) исходной задачи 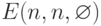. Для получения всех решений этой задачи остается лишь взять объединение по i множеств otv(i).

При анализе трудоемкости алгоритма получаем, что глубина рекурсии равна n² - при каждом рекурсивном вызове по j (j=0,1,...n-1) происходит n рекурсивных вызовов по i (i=0,1,...n-1).

//нахождение одного варианта расстановки
#include "stdafx.h"
#include <iostream>
using namespace std;
void Initialization(int n, int ***x);
void Destruction(int n, int **x);
bool Queen(int n, int **x);
void Placement(int n, int **a, int *p, int *h, int *du, 
               int *dd, int i=0, int j=0);

int _tmain(int argc, _TCHAR* argv[]){
  int n, i, j;
  bool otv;
  int **mas;
  printf("Введите размер шахматной доски n : ");
  scanf ("%d",&n);
  Initialization(n,&mas);
  otv = Queen(n,mas);
  if ( otv ) printf("Правильное размещение найдено\n");
  else printf("Правильного размещения не найдено\n");
  Destruction(n,mas);
  system("pause");
  return 0;
}

//инициализация поля шахматной доски
void Initialization(int n, int ***x){ 
  *x = new int*[n]; 
  for (int i = 0 ; i < n; i++ ){
    (*x)[i] = new int[n];
    for (int j = 0 ; j < n ; j++ )
      (*x)[i][j] = 0;
  }
} 

//вывод найденной расстановки в файл
void Destruction(int n, int **x){ 
  FILE *f;
  if( ( f = fopen("out.txt","w") ) == NULL ){
    printf("Файл out.txt не может быть открыт для записи");
  }
    else{
      fprintf(f,"%d\n",n);
      for (int i = 0 ; i < n; i++ ){
        for (int j = 0 ; j < n ; j++ )
          fprintf(f,"%2d",x[i][j]);
        fprintf(f,"\n");
      }
    }
  for (int i = 0 ; i < n; i++ )
    delete [] x[i];
  delete [] x;
} 

//проверка возможности постановки ферзя
bool Queen(int n, int **x){
  bool rez = false;
  int *p, *h, *du, *dd;
  p = new int[n];
  h = new int[n];
  du = new int[2 * n - 1];
  dd = new int[2 * n - 1];
  for ( int i = 0 ; i < n ; i++ )
    p[i] = h[i] = 0;
  for ( int i = 0 ; i < (2 * n - 1) ; i++ )
    du[i] = dd[i] = 0;
  Placement(n,x,p,h,du,dd);
  if ( h[0] != 0 ) rez = true;
  delete [] dd, du, h, p;
  return rez;
}

//описание функции расстановки ферзей
void Placement(int n, int **a, int *p, int *h, int *du, 
               int *dd, int i, int j){
  if ( j >= 0 && j < n )
    if ( i < n )
      if (h[i]==0 && du[i+j] == 0 && dd[n+i-j-1] == 0 ) {
        h[i] = 1;
        du[i+j] = 1;
        dd[n+i-j-1] = 1;
        p[j] = i;
        a[i][j] = 1;
        Placement(n,a,p,h,du,dd,0,j+1);
      }
      else
        Placement(n,a,p,h,du,dd,i+1,j);
    else
      if ( j > 0 ) {
        h[p[j-1]] = 0;
        du[p[j-1]+j-1] = 0;
        dd[n+p[j-1]-(j-1)-1] = 0;
        a[p[j-1]][j-1] = 0;
        Placement(n,a,p,h,du,dd,p[j-1]+1,j-1);
      }
}

Пример 2. Задача о количестве расстановок ферзей на шахматной доске.

Составить рекурсивную функцию, находящую количество возможных расстановок n ферзей на шахматной доске размером nxn так, чтобы они не били друг друга.

Предложенную задачу можно решать по приведенным в Примере 1 функциям, упростив их следующим образом. Вместо запоминания найденных решений будем подсчитывать в переменной otv их количество.

Пример 3. Задача об основных расстановках.

Для формулировки следующей задачи введем понятие. Среди всех расстановок n ферзей на доске nxn выделим отдельные непересекающиеся классы H_s (s=0,1,...,q) расстановок так, что все элементы данного класса можно получить из любого его представителя какими-либо элементарными преобразованиями типа:

• поворот доски в ее плоскости вокруг центра на 90 , 180 и 270 ;
• преобразования симметрии относительно диагоналей;
• преобразования симметрии относительно прямых, проходящих через центр доски по границам клеток.

Взяв по одному представителю из каждого класса H_s (s=0,1,...,q), получим некоторое множество, называемое основными расстановками. Составить рекурсивную функцию, находящую какое-либо множество основных расстановок n ферзей на шахматной доске размера nxn.

Эта задача решается с помощью рекурсивных функций практически аналогично задаче из Примера 1. Отличия здесь такие. Рекурсивная функция последовательно формирует каждую из возможных расстановок ферзей на доске, но не все из них запоминаются в матрице ответа otv. Очередная полученная расстановка подвергается проверке - включать или не включать ее в матрицу otv. Делается это следующим образом. Из вектора pos описанными выше элементарными преобразованиями формируются еще семь расстановок (некоторые из них могут оказаться совпадающими). Если ни одна из них не входит в текущую матрицу ответов otv, то otv дополняется новым решением и так далее. Следовательно, по завершении вычислений otv будет содержать некоторое множество основных расстановок.

Ключевые термины

Возвратная рекурсия – это соединение метода перебора с возвратом и рекурсии.

Детерминированный алгоритм – это алгоритм, который однозначно осуществит выбор конкретной альтернативы и продолжит работать в соответствии с эти выбором.

Исчерпывающий поиск – это процесс нахождения в некотором множестве всех возможных вариантов, среди которых имеется решение конкретной задачи.

Метод решета – это один из методов организации исчерпывающего поиска, при котором из множества возможных вариантов исключаются все элементы, не являющиеся решениями.

Недетерминированный алгоритм – это алгоритм, который исследует все возможности одновременно, как бы копируя себя для реализации вычислений по всем альтернативам одновременно.

Перебор с возвратом (backtracking) – это один из методов организации исчерпывающего поиска, который строится конструктивно последовательным расширением частичного решения.

Полное решение – это набор вариантов, образующий хотя бы одно решение в целом.

Частичное решение – это неполный набор вариантов, который входит в одно или несколько полных решений.

Краткие итоги

1. Решение переборных задач сводится к определению наличия решения, всех различных вариантов решения или к нахождению одного решения.
2. В зависимости от постановки задачи переборные алгоритмы реализуются методами перебора с возвратом или методом решета.
3. Возвратная рекурсия – это соединение метода перебора с возвратом и рекурсии.
4. Детерминированный алгоритм однозначно осуществит выбор конкретной альтернативы и продолжит работать в соответствии с эти выбором. Недетерминированный алгоритм исследует все возможности одновременно, как бы копируя себя для реализации вычислений по всем альтернативам одновременно.
5. Для решения задачи о расстановке ферзей на шахматной доске как альтернативный используется метод возвратной рекурсии.
6. При разработке триады для решения задачи о расстановке ферзей вводятся дополнительные параметры при описании процесса расстановки.
7. Базой в данной задаче считается совокупность всех тупиковых ситуаций.
8. Декомпозиция проводится от частичного к полному решению или к снятию ферзя с вертикали (возврат).