Алгоритмы сжатия данных
Цель лекции: изучить основные виды и алгоритмы сжатия данных и научиться решать задачи сжатия данных по методу Хаффмана и с помощью кодовых деревьев.
Основоположником науки о сжатии информации принято считать Клода Шеннона. Его теорема об оптимальном кодировании показывает, к чему нужно стремиться при кодировании информации и насколько та или иная информация при этом сожмется. Кроме того, им были проведены опыты по эмпирической оценке избыточности английского текста. Шенон предлагал людям угадывать следующую букву и оценивал вероятность правильного угадывания. На основе ряда опытов он пришел к выводу, что количество информации в английском тексте колеблется в пределах 0,6 – 1,3 бита на символ. Несмотря на то, что результаты исследований Шеннона были по-настоящему востребованы лишь десятилетия спустя, трудно переоценить их значение.
Сжатие данных – это процесс, обеспечивающий уменьшение объема данных путем сокращения их избыточности. Сжатие данных связано с компактным расположением порций данных стандартного размера. Сжатие данных можно разделить на два основных типа:
- Сжатие без потерь (полностью обратимое) – это метод сжатия данных, при котором ранее закодированная порция данных восстанавливается после их распаковки полностью без внесения изменений. Для каждого типа данных, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.
- Сжатие с потерями – это метод сжатия данных, при котором для обеспечения максимальной степени сжатия исходного массива данных часть содержащихся в нем данных отбрасывается. Для текстовых, числовых и табличных данных использование программ, реализующих подобные методы сжатия, является неприемлемыми. В основном такие алгоритмы применяются для сжатия аудио- и видеоданных, статических изображений.
Алгоритм сжатия данных (алгоритм архивации) – это алгоритм, который устраняет избыточность записи данных.
Введем ряд определений, которые будут использоваться далее в изложении материала.
Алфавит кода – множество всех символов входного потока. При сжатии англоязычных текстов обычно используют множество из 128 ASCII кодов. При сжатии изображений множество значений пиксела может содержать 2, 16, 256 или другое количество элементов.
Кодовый символ – наименьшая единица данных, подлежащая сжатию. Обычно символ – это 1 байт, но он может быть битом, тритом {0,1,2}, или чем-либо еще.
Кодовое слово – это последовательность кодовых символов из алфавита кода. Если все слова имеют одинаковую длину (число символов), то такой код называется равномерным (фиксированной длины), а если же допускаются слова разной длины, то – неравномерным (переменной длины).
Код – полное множество слов.
Токен – единица данных, записываемая в сжатый поток некоторым алгоритмом сжатия. Токен состоит из нескольких полей фиксированной или переменной длины.
Фраза – фрагмент данных, помещаемый в словарь для дальнейшего использования в сжатии.
Кодирование – процесс сжатия данных.
Декодирование – обратный кодированию процесс, при котором осуществляется восстановление данных.
Отношение сжатия – одна из наиболее часто используемых величин для обозначения эффективности метода сжатия.
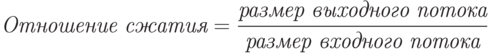
Коэффициент сжатия – величина, обратная отношению сжатия.
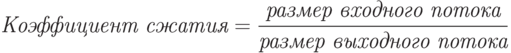
Средняя длина кодового слова – это величина, которая вычисляется как взвешенная вероятностями сумма длин всех кодовых слов.
Lcp=p1L1+p2L2+...+pnLn,
где – вероятности кодовых слов;
L1,L2,...,Ln – длины кодовых слов.
Существуют два основных способа проведения сжатия.
Статистические методы – методы сжатия, присваивающие коды переменной длины символам входного потока, причем более короткие коды присваиваются символам или группам символам, имеющим большую вероятность появления во входном потоке. Лучшие статистические методы применяют кодирование Хаффмана.
Словарное сжатие – это методы сжатия, хранящие фрагменты данных в "словаре" (некоторая структура данных). Если строка новых данных, поступающих на вход, идентична какому-либо фрагменту, уже находящемуся в словаре, в выходной поток помещается указатель на этот фрагмент. Лучшие словарные методы применяют метод Зива-Лемпела.
Рассмотрим несколько известных алгоритмов сжатия данных более подробно.
Метод Хаффмана
Этот алгоритм кодирования информации был предложен Д.А. Хаффманом в 1952 году. Хаффмановское кодирование (сжатие) – это широко используемый метод сжатия, присваивающий символам алфавита коды переменной длины, основываясь на вероятностях появления этих символов.
Идея алгоритма состоит в следующем: зная вероятности вхождения символов в исходный текст, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью присваиваются более короткие коды. Таким образом, в этом методе при сжатии данных каждому символу присваивается оптимальный префиксный код, основанный на вероятности его появления в тексте.
Префиксный код – это код, в котором никакое кодовое слово не является префиксом любого другого кодового слова. Эти коды имеют переменную длину.
Оптимальный префиксный код – это префиксный код, имеющий минимальную среднюю длину.
Алгоритм Хаффмана можно разделить на два этапа.
- Определение вероятности появления символов в исходном тексте.
Первоначально необходимо прочитать исходный текст полностью и подсчитать вероятности появления символов в нем (иногда подсчитывают, сколько раз встречается каждый символ). Если при этом учитываются все 256 символов, то не будет разницы в сжатии текстового или файла иного формата.
- Нахождение оптимального префиксного кода.
Далее находятся два символа a и b с наименьшими вероятностями появления и заменяются одним фиктивным символом x, который имеет вероятность появления, равную сумме вероятностей появления символов a и b. Затем, используя эту процедуру рекурсивно, находится оптимальный префиксный код для меньшего множества символов (где символы a и b заменены одним символом x ). Код для исходного множества символов получается из кодов замещающих символов путем добавления 0 или 1 перед кодом замещающего символа, и эти два новых кода принимаются как коды заменяемых символов. Например, код символа a будет соответствовать коду x с добавленным нулем перед этим кодом, а для символа b перед кодом символа x будет добавлена единица.
Коды Хаффмана имеют уникальный префикс, что и позволяет однозначно их декодировать, несмотря на их переменную длину.
Пример 1. Программная реализация метода Хаффмана.
#include "stdafx.h"
#include <iostream>
using namespace std;
void Expectancy();
long MinK();
void SumUp();
void BuildBits();
void OutputResult(char **Result);
void Clear();
const int MaxK = 1000;
long k[MaxK + 1], a[MaxK + 1], b[MaxK + 1];
char bits[MaxK + 1][40];
char sk[MaxK + 1];
bool Free[MaxK + 1];
char *res[256];
long i, j, n, m, kj, kk1, kk2;
char str[256];
int _tmain(int argc, _TCHAR* argv[]){
char *BinaryCode;
Clear();
cout << "Введите строку для кодирования : ";
cin >> str;
Expectancy();
SumUp();
BuildBits();
OutputResult(&BinaryCode);
cout << "Закодированная строка : " << endl;
cout << BinaryCode << endl;
system("pause");
return 0;
}
//описание функции обнуления данных в массивах
void Clear(){
for (i = 0; i < MaxK + 1; i++){
k[i] = a[i] = b[i] = 0;
sk[i] = 0;
Free[i] = true;
for (j = 0; j < 40; j++)
bits[i][j] = 0;
}
}
/*описание функции вычисления вероятности вхождения каждого символа в тексте*/
void Expectancy(){
long *s = new long[256];
for ( i = 0; i < 256; i++)
s[i] = 0;
for ( n = 0; n < strlen(str); n++ )
s[str[n]]++;
j = 0;
for ( i = 0; i < 256; i++)
if ( s[i] != 0 ){
j++;
k[j] = s[i];
sk[j] = i;
}
kj = j;
}
/*описание функции нахождения минимальной частоты символа в исходном тексте*/
long MinK(){
long min;
i = 1;
while ( !Free[i] && i < MaxK) i++;
min = k[i];
m = i;
for ( i = m + 1; i <= kk2; i++ )
if ( Free[i] && k[i] < min ){
min = k[i];
m = i;
}
Free[m] = false;
return min;
}
//описание функции подсчета суммарной частоты символов
void SumUp(){
long s1, s2, m1, m2;
for ( i = 1; i <= kj; i++ ){
Free[i] = true;
a[i] = 0;
b[i] = 0;
}
kk1 = kk2 = kj;
while (kk1 > 2){
s1 = MinK();
m1 = m;
s2 = MinK();
m2 = m;
kk2++;
k[kk2] = s1 + s2;
a[kk2] = m1;
b[kk2] = m2;
Free[kk2] = true;
kk1--;
}
}
//описание функции формирования префиксных кодов
void BuildBits(){
strcpy(bits[kk2],"1");
Free[kk2] = false;
strcpy(bits[a[kk2]],bits[kk2]);
strcat( bits[a[kk2]] , "0");
strcpy(bits[b[kk2]],bits[kk2]);
strcat( bits[b[kk2]] , "1");
i = MinK();
strcpy(bits[m],"0");
Free[m] = true;
strcpy(bits[a[m]],bits[m]);
strcat( bits[a[m]] , "0");
strcpy(bits[b[m]],bits[m]);
strcat( bits[b[m]] , "1");
for ( i = kk2 - 1; i > 0; i-- )
if ( !Free[i] ) {
strcpy(bits[a[i]],bits[i]);
strcat( bits[a[i]] , "0");
strcpy(bits[b[i]],bits[i]);
strcat( bits[b[i]] , "1");
}
}
//описание функции вывода данных
void OutputResult(char **Result){
(*Result) = new char[1000];
for (int t = 0; i < 1000 ;i++)
(*Result)[t] = 0;
for ( i = 1; i <= kj; i++ )
res[sk[i]] = bits[i];
for (i = 0; i < strlen(str); i++)
strcat( (*Result) , res[str[i]]);
}
Листинг
.
Алгоритм Хаффмана универсальный, его можно применять для сжатия данных любых типов, но он малоэффективен для файлов маленьких размеров (за счет необходимости сохранения словаря). В настоящее время данный метод практически не применяется в чистом виде, обычно используется как один из этапов сжатия в более сложных схемах. Это единственный алгоритм, который не увеличивает размер исходных данных в худшем случае (если не считать необходимости хранить таблицу перекодировки вместе с файлом).
