Одномерные массивы: задачи сортировок элементов массива

Сортировка методом простого выбора (простой перебор)

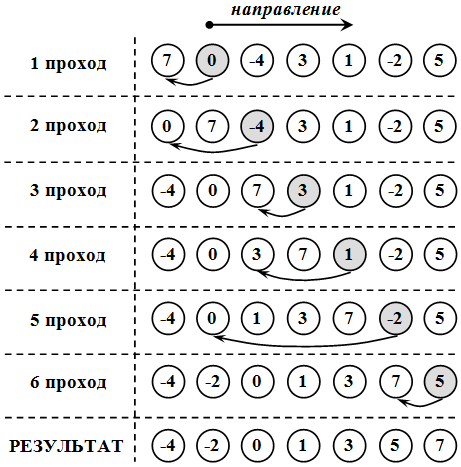
Это наиболее естественный алгоритм упорядочивания. При данной сортировке из массива выбирается элемент с наименьшим значением и обменивается с первым элементом. Затем из оставшихся n - 1 элементов снова выбирается элемент с наименьшим ключом и обменивается со вторым элементом, и т.д. ( рис. 12.2)

Шаги алгоритма:

1. находим минимальное значение в текущей части массива;
2. производим обмен этого значения со значением на первой неотсортированной позиции;
3. далее сортируем хвост массива, исключив из рассмотрения уже отсортированные элементы.

Рис. 12.2. Демонстрация сортировки по неубыванию методом простого выбора

//Описание функции сортировки методом простого выбора
void SelectionSort (int k,int x[max]) {
  int i,j,min,temp;
  for (i=0;i<k-1;i++) {
  //устанавливаем начальное значение минимального индекса
    min=i; 
    //находим минимальный индекс элемента
    for (j=i+1;j<k;j++){
      if (x[j]<x[min])
        min=j;
      //меняем значения местами 
      }
      temp=x[i];
      x[i]=x[min];
      x[min]=temp;
  }
}

Как и в пузырьковой сортировке, внешний цикл выполняется n-1 раз, а внутренний – в среднем n/2 раз. Следовательно, сортировка методом простого выбора требует

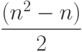
Сортировка методом простого включения (сдвиг-вставка, вставками, вставка и сдвиг)

Хотя этот метод сортировки намного менее эффективен, чем сложные алгоритмы (такие как быстрая сортировка), у него есть ряд преимуществ:

• прост в реализации;
• эффективен на небольших наборах данных, на наборах данных до десятков элементов может оказаться лучшим;
• эффективен на наборах данных, которые уже частично отсортированы;
• это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы);
• может сортировать массив по мере его получения;
• не требует временной памяти, даже под стек.

На каждом шаге алгоритма выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированной последовательности до тех пор, пока набор входных данных не будет исчерпан. Метод выбора очередного элемента из исходного массива произволен; может использоваться практически любой алгоритм выбора ( рис. 12.3).

Рис. 12.3. Демонстрация сортировки по неубыванию методом простого включения

//Описание функции сортировки методом простого включения
void InsertSort (int k,int x[max]) {
  int i,j, temp;
  for (i=0;i<k;i++) {
  //цикл проходов, i - номер прохода
    temp=x[i]; 
    //поиск места элемента
    for (j=i-1; j>=0 && x[j]>temp; j--)
      x[j+1]=x[j];//сдвигаем элемент вправо, пока не дошли
      //место найдено, вставить элемент 
      x[j+1]=temp;  
  }
}

В отличие от пузырьковой сортировки и сортировки простого выбора, количество сравнений в сортировке вставками зависит от изначальной упорядоченности списка. Если список уже отсортирован, количество сравнений равно n-1 ; в противном случае его производительность является величиной порядка n².

Ключевые термины

Ключ сортировки – это часть данных, определяющая порядок элементов.

Сортировка – это упорядочивание набора однотипных данных по возрастанию или убыванию.

Сортировка методом "пузырька" – это алгоритм попарного сравнения элементов одномерного массива.

Сортировка методом простого включения – это алгоритм последовательного помещения элемента массива в отсортированную часть в соответствии с ключом сортировки.

Сортировка методом простого выбора – это алгоритм последовательного обмена минимального и первого элементов неотсортированной части массива.

Краткие итоги

1. Задачи сортировок массивов имеют широкое прикладное значение.
2. Существует большое количество алгоритмов сортировок массивов, различающихся трудоемкостью.
3. При оценке трудоемкости алгоритмов учитываются критерии: количество сравнений и перестановок, время в лучшем и худшем случаях, естественность поведения.
4. К алгоритмам простых сортировок относятся: сортировка методом "пузырька", сортировка методом простого выбора, сортировка методом простого включения.
5. Простые сортировки эффективны на небольших объемах данных.