Системы компьютерной математики (СКМ)
12.4. Решение дифференциальных уравнений в СКМ
Решение дифференциальных уравнений (ДУ) является одной из самых сложных задач математики. Она возникает практически во всех областях знаний: в науке, в технике, в экономике. Как известно, дифференциальные уравнения делятся на обыкновенные (ОДУ) и дифференциальные уравнения в частных производных – по-другому их называют уравнениями математической физики. Последние и представляют более общий инструмент исследования, но большие трудности в их решении заставляют, по возможности, применять аппарат ОДУ. Это нашло отражение в средствах пакетов СКМ и, в частности, в MathCad, где приводится мощный и разнообразный аппарат работы с ОДУ.
Методы их численного решения глубоко разработаны в вычислительной математике, широко алгоритмизированы и представлены в MathCad практически в полном объеме. Поэтому не будем подробно останавливаться на этой теме, а перейдем к аналитическим методам решения ДУ в MathCad.
Сразу отметим, что в СКМ Mathematica и Marpl имеются встроенные блоки решения ОДУ в символьной форме; разработчики КСМ MathCad пошли другим путем: специального обособленного инструмента решения ОДУ в ней нет. Для решения ОДУ предлагается последовательно применять набор встроенных операторов. Ниже покажем, что это не является недостатком этого пакета.
Большинство практических задач может быть сведено к аппарату линейных систем ДУ (ЛОДУ). С одной стороны, методы их аналитического решения и анализа хорошо разработаны и широко известны, а нелинейность в большинстве случаев можно исключить, разбив общую задачу на ряд частных подзадач без большого ущерба для точности.
Известно, что решение ЛОДУ в общем виде равно сумме общего решения однородного ЛОДУ (с нулевой правой частью), и какого-либо частного решения неоднородного ЛОДУ.
Покажем, как эта задача решается в СКМ Mathematica 5, где имеются встроенные блоки решения ОДУ. Для решения ЛОДУ используют встроенную функцию DSolve[ ] следующим образом.
![DSolve[x''[t]+4x'[t]==10Sin[2t],x[t],t]](/sites/default/files/tex_cache/a31f597334458e906151474fa3c0bf95.png)
После исполнительной команды – одновременного нажатия клавиш Shift и Enter, сразу получим результат:
![DSolve[x''[t]+4x'[t]==10Sin[2t],x[t],t]](/sites/default/files/tex_cache/a31f597334458e906151474fa3c0bf95.png)
![{{x[t] \to -1/4e^{-4t}C[1]+C[2]-Cos[2t]-1/2Sin[2t]}}](/sites/default/files/tex_cache/1f65a4c8730ab91f3da7e62955a0830b.png)
Обратите внимание на несколько необычный способ записи функций: при помощи квадратных скобок; но это, равно как и исполнительная команда на выполнение вычислений одновременным нажатием клавиш Shift и Enter, – специфические особенности СКМ Mathematica.
Для решения подобного уравнения СКМ MathСad, где такие решающие блоки отсутствуют, рекомендуется применять операторные методы – прямое и обратное преобразование Лапласа или Фурье. Напомним, что смысл этого метода заключается в переходе от искомой функции, называемой оригиналом, к особым интегральным функциям комплексного переменного  – так называемым изображениям, в результате чего после подстановки изображения вместо оригинала в линейное ДУ операция дифференцирования относительно новой переменной заменяется операцией умножения на соответствующий новый аргумент
– так называемым изображениям, в результате чего после подстановки изображения вместо оригинала в линейное ДУ операция дифференцирования относительно новой переменной заменяется операцией умножения на соответствующий новый аргумент  , а само ДУ
, а само ДУ  -й степени преобразуется в многочлен этой же степени относительно
-й степени преобразуется в многочлен этой же степени относительно  , называемый характеристическим. Определив корни характеристического многочлена и выполнив обратный переход от изображения к оригиналу при помощи обратного преобразования Лапласа или Фурье, соответственно, легко можно отыскать решение исходного ДУ.
, называемый характеристическим. Определив корни характеристического многочлена и выполнив обратный переход от изображения к оригиналу при помощи обратного преобразования Лапласа или Фурье, соответственно, легко можно отыскать решение исходного ДУ.
Конкретные действия для решения указанной задачи следующие.
Пусть дано исходное ЛОДУ:
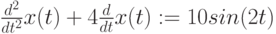
Его необходимо записать в форме с нулевой правой частью:
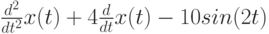 |
( **) |
Вызывать с панели Symbolic оператор laplace и задать исполнение  :
:
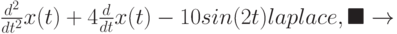
в результате получается малопонятное выражение, в котором обозначим изображение функции одной буквой, например, h, выражения для начальных значений функции и первой производной заменим, например, на Х0 и Х10, соответственно. После всех этих преобразований и замен будет получено следующее выражение:
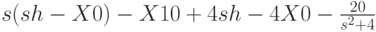
Очень неудобно. Беда еще, к сожалению, в том, что оператор laplace иногда отказывается работать.
Поэтому проще самим написать изображение для уравнения (**) без помощи оператора laplace. При этом производные заменяются изображениями согласно известной теореме по образцу, приведенному в таблице 12.2.
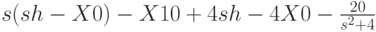
| Производные оригинала | Изображение производной |
|---|---|
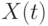 |
 |
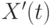 |
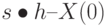 |
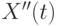 |
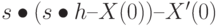 |
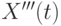 |
 |
Здесь через  ,
, 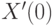 ,
, 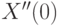 обозначены начальные условия для производных указанных порядков, в нашем примере они обозначены согласно таблице 12.3.
обозначены начальные условия для производных указанных порядков, в нашем примере они обозначены согласно таблице 12.3.
| Начальные условиядля производных | Обозначения в рассматриваемом примере |
|---|---|
 |
 |
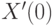 |
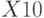 |
Продолжить таблицу 2 в случае необходимости не представляет труда – последующая строка легко получается из предыдущей.
Далее при самостоятельном задании изображения для уравнения (**) к правой части уравнения (*) отдельно применим оператор laplace:

Подставим в исходное уравнение (**) и получим следующее выражение:
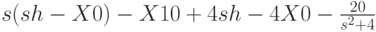
Разрешим это уравнение относительно  оператором solve и применим обратное преобразование Лапласа
оператором solve и применим обратное преобразование Лапласа 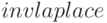 (оба с панели Symbolic)
(оба с панели Symbolic)


Это и есть решение ЛОДУ (*), отличия от решения СКМ Mathematica – в форме представления постоянной интегрирования. В последнем случае оно содержат начальные условия в явном виде.
