Системы компьютерной математики (СКМ)
12.3. Создание документа и общие приемы работы СКМ MathCad
Главное меню и общие традиционные панели Windows: "Стандартная" и "Форматирование". Перечислим основные возможности среды MathCad.
Общие возможности
- Разработка и редактирование документов, содержащих как математические формулы любой сложности, так и все встроенные инструменты среды MathCad. Подготовка этих документов к изданию или передаче по сети Internet.
- Использование общепринятого расширяемого языка разметки XML как универсального способа организации обмена данными с другими приложениями. Это позволяет преобразовывать файлы MathCad в HTML-страницы и в формат PDF.
- Возможность вставки в документ широкого спектра объектов (см. рис.12.3.)
- Разработка веб-документов и сетевые возможности по их пересылке, получению обновлений и поддержки.
- Получение документов MathCad по сети и выполнение расчетов в этих документах.
- Получение через Internet и подключение новых книг расширения для реализации дополнительных возможностей среды MathCad.
- Доступный официальный форум.
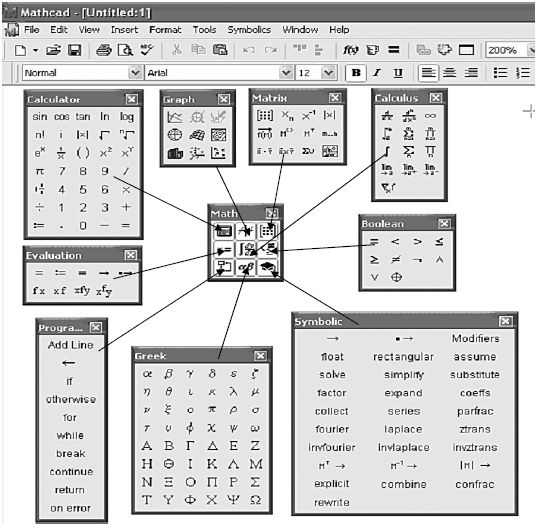
Все математические действия выполняются при помощи девяти палитр (панелей инструментов), вызываемых, в свою очередь, из панели Мath. Они-то и позволяют получить полный букет всевозможных операторов и команд среды MathCad.
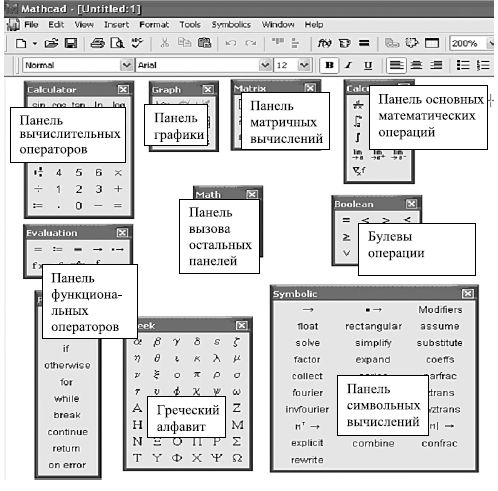
Эти девять панелей представлены на рис.12.3, а на рис.12.4 показано назначение этих панелей.
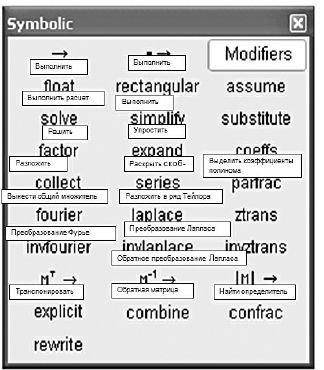
Интерфейс этих панелей отличается продуманностью и дружелюбием. Пока понадобятся только три: Сalculator, Сalculus, Symbolic – их и оставим, а остальные закроем. Панель Symbolic – основная панель инструментов для выполнения символьных вычислений. На рис.12.5 приводятся все ее элементы и их назначение.
Продемонстрируем простой пример — найдем сумму известного бесконечного ряда:

по формуле ![\sum_{n=1}^{\infty} \left[(-1)^{n-1}\cdot \left(\frac{1}{2\cdot n -1} \right) \right]](/sites/default/files/tex_cache/6ce9c83d718fb96e9bc820dfd86b2c5e.png)
Для этого нужно последовательно: вызвать с панели Calculus вот такой символ 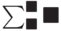 и заполнить знакоместа суммы
и заполнить знакоместа суммы 
(везде далее математические записи приводятся в том виде, как они выглядят в документе MathCad, откуда они и скопированы). Теперь следует выполнить такие действия.
Ввести формулу ![\sum_{n=1}^{\infty} \left[(-1)^{n-1}\cdot \left(\frac{1}{2\cdot n -1} \right) \right]](/sites/default/files/tex_cache/6ce9c83d718fb96e9bc820dfd86b2c5e.png) при помощи панели Calculator
при помощи панели Calculator
С панели Symbolic вызвать оператор символьных преобразований  и нажать клавишу Enter.
и нажать клавишу Enter.
![\sum_{n=1}^{\infty} \left[(-1)^{n-1}\cdot \left(\frac{1}{2\cdot n -1} \right) \right] \to \frac {\pi}{4}](/sites/default/files/tex_cache/c5a8e8f965745c2db7158349de060b2a.png)
Результат верный. А ведь мы не набрали ни строчки кода – все делали методом визуального программирования, выбирая нужное с панелей.
Теперь просуммируем такой гармонический ряд:

который, как известно, расходится, но если уменьшить его на самую малость – должен сойтись:
Повторим все манипуляции с панелью Symbolic и получим маловразумительный результат
![\lim_{n\to\infty} \left[ \left(\sum_{i=1}^{n}\frac{1}{i}\right) - ln(n) \right] \to \gamma](/sites/default/files/tex_cache/c80336ca27be93d38608fb87f1bd83a0.png) float, 10
float, 10 
Теперь понятно: это – постоянная Эйлера (она же – третий замечательный предел, обозначаемая как число "С"). Чтобы отбросить все сомнения, закажем ее поточнее, например, до 250 значащих цифр.

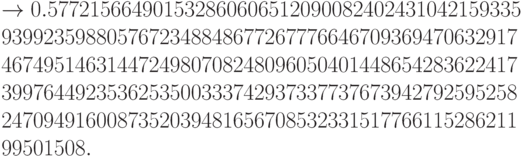
К сожалению, в доступной автору литературе в полном виде эти данные не встречались, а попытки вычислить ее значение "в лоб", например, на С++ в формате данных double, дали только 64 значащие цифры, остальные 186 знаков – на совести разработчиков MathCad.