Системы компьютерной математики (СКМ)
Здесь нетрудно догадаться, что в символике MathCad  и
и 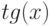 изображаются как
изображаются как 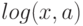 и
и  соответственно. Успешно решается и более сложный пример:
соответственно. Успешно решается и более сложный пример:

А вот совсем простую задачу:
![\lim_{\delta \to 0} \frac{\left[(x+\delta)^n-x^n \right]}{\delta}](/sites/default/files/tex_cache/34fc22bff70577ce7ae213b79b0573e2.png)
в общем виде решить не получается – нужно задать конкретное значение  .
.
Для показательной функции 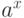 :
:
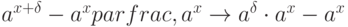
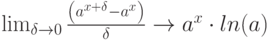
А теперь еще забавней – проинтегрируем функцию:
по определению через предел интегральной суммы. Здесь особенность – верхний предел зададим параметрически через  . Для этого составим интегральную сумму:
. Для этого составим интегральную сумму:
![\lim_{n \to \infty} \sum_{k=0}^n \left[ \left( \frac{x}{n} \right) \cdot a^{x{\frac{k}{n}}} \right]](/sites/default/files/tex_cache/d5dd357be1527538e3a96fb491dbc10b.png)
![\lim_{n \to \infty} \sum_{k=0}^n \left[ \left( \frac{x}{n} \right) \cdot a^{x{\frac{k}{n}}} \right] \to \frac{a^x-1}{ln(a)}](/sites/default/files/tex_cache/80f7b192b1cdfa21bb7eaf69bcab4241.png)
При этом все константы следует собрать вместе в постоянную интегрирования  :
:

и тогда имеем первообразную, а заодно и красивую демонстрацию теоремы Ньютона-Лейбница.
Теперь вычисление суммы ряда. Все очень просто и правильно:

Воспользуемся известным многим поколениям абитуриентов пособием СканавиС.И.[ 8] – задача № 4.077 из раздела "В", решение которой показывает не только "более высокое качество усвоения школьной программы <...> но и позволит экзаменующемуся обнаружить способность к самостоятельному логическому мышлению" [9].
![\sum_{n=1}^{m} \left[n \left(2^n \right) \right] \to 2^{m+1} \cdot (m-1) -\frac{m(m+1)}{2}+2](/sites/default/files/tex_cache/1ea40ca6ef12110add86755f6e248fda.png)
Рассмотрим разложение в ряд Тейлора. Оно выполняется при помощи оператора Series c панели Simbolic. В маркеры оператора Series последовательно заносятся через запятую: исходная функция, имя аргумента, количество членов ряда.
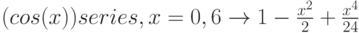
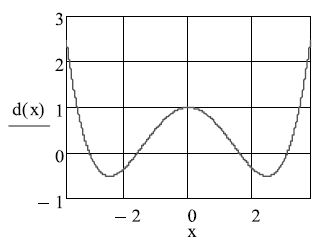
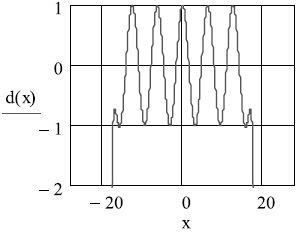
Теперь зададим 44 члена
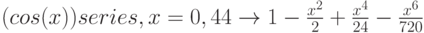
Решение уравнений – одна из самых актуальных и одновременно самых сложных задач в среде MathCad. Оно может быть выполнено аналитически, численно или графическим способом. Аналитический способ решения предпочтителен, поскольку, не говоря об отсутствии погрешностей вычисления, его вид позволяет детально проанализировать результаты и легко и наглядно использовать их в последующих исследованиях либо в практических целях. К сожалению, возможность аналитического решения диктует жесткие условия, которые мы не будем обсуждать. Отметим, например, что переменные должны быть в степени не выше четвертой (за исключением частных случаев), а используемые функции – одинакового вида. На практике, в прикладных задачах, любое соотношение, полученное в виде композиции элементарных функций (а не как решение сложной системы дифференциальных уравнений), является ярким событием. Вся масса уравнений, приводимых в учебных пособиях, является материалом, специально подобранным в чисто учебных целях.
Самым универсальным способом решения уравнений является графический, возможности использования которого в MathCad обширны.
Найдем в общем виде корни полиномиального уравнения одной переменной (степенного многочлена) – это наиболее часто встречающаяся практическая задача. Зададим исходный полином четвертой степени
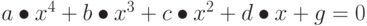
Среда MathCad выполняет поиск решения уравнения одной переменой посредством оператора salve c панели "Simbolic". Задача успешно выполняется, и хотя выдается сообщение, что не хватает ресурсов для вывода решения на экран, и полюбоваться им нельзя,
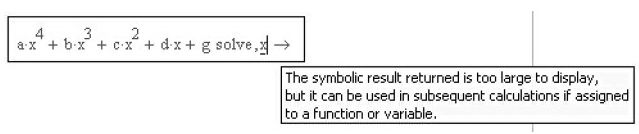
но само решение получено и для дальнейших вычислений им можно пользоваться.
Попробуем получить это решение другим способом: через пункт Simbolic главного меню. Решение получено и в этом случае выводится на экран, но его размеры (более 40-ка страниц текста) превышают возможности буфера ОС, и даже скопировать его по частям не удается. Так проявляется еще одна проблема символьных расчетов, особенно для решений в общем виде – громоздкие выражения, как правило, неудобные для анализа и последующих преобразований. Выход – упрощать выражения, например, разложением в степенные ряды.
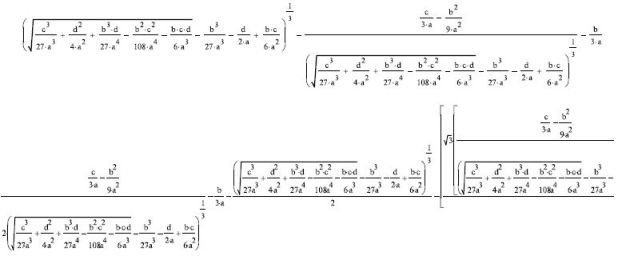
Как иллюстрация, на рис.12.6 приводится для кубического уравнения: формула для одного из корней – целиком, а для другого корня – только фрагмент формулы. Размеры и здесь впечатляют.
Теперь попробуем решить полиномиальное уравнение с заданными постоянными коэффициентами. Составим заготовку
 |
( *) |
и при помощи оператора expand получим полином:
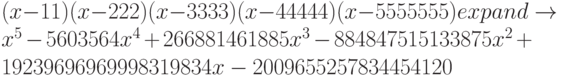
Полученные коэффициенты перенесем через буфер ОС в текстовый файл .txt, созданный, например, при помощи приложения ОС "Блокнот", а оттуда вернем обратно через буфер ОС в MathCad, который перед тем перезагрузим, чтобы исключить возможность "подсказки" (заодно убедимся, как легко и удобно переносить числа в текстовый документ и обратно. А вот простейшее выражение, содержащее, например, символ радикала, запомнить можно, но вернуть не получится).
Никаких трудностей не возникло, хотя размеры чисел значительно превосходят представление данных целого типа для многих алгоритмических языков высокого уровня. Даже в случае полинома пятой степени решение легко получается в символьном виде, для этого следует: вставить оператор solve c панели Symbolic, через запятую указать имя аргумента " " и нажать Enter.
" и нажать Enter.
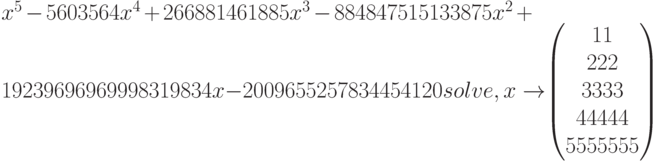
В том, что решение найдено именно в символьном виде, а не численно, легко убедиться, записав исходный полином с иррациональными корнями, например:
-
Подготовим полином:
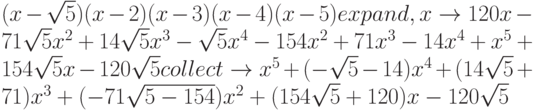
-
Найдем решение:

Очевидно, что ответ получен в символьной форме.
По данным [6], СКМ MathCad при аналитическом решении сначала пытается найти ответ в символьном виде, а в случае неудачи переходит к численному решению задачи автоматически.
Решение неравенств считается одной из самых сложных тем школьной математики, поскольку требует не только навыков выполнения математических преобразования, но и умения логически анализировать поведение функций в области допустимых значений.
Пример, неверно решаемый в СКМ MathCad 13:
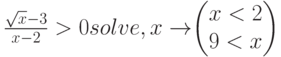
Х должен быть не меньше  ; правильно он решен в СКМ MathCad 14, да и ответ выглядит привлекательней:
; правильно он решен в СКМ MathCad 14, да и ответ выглядит привлекательней:
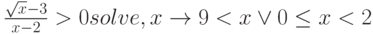
Рассмотрим аналитическое дифференцирование. Поскольку производная любой элементарной функции может быть определена по жестко установленному алгоритму, среда MathCad всегда с успехом это выполняет. Вызовем оператор дифференцирования
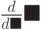
с панели Symbolic и занесем в него исходное выражение 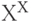 :
:

результат получается после выполнения оператора  .
.
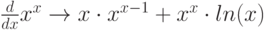
Проверим
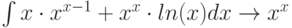
В случае аналитического интегрирования сложнее: и жестко заданного алгоритма нет, и, вообще, в элементарных функциях не для каждой существует первообразная. Интегрирование – это искусство. MathCad и здесь на высоте. Хотя при решении следующего интеграла в общем виде выдается только один вариант (для действительных корней знаменателя),
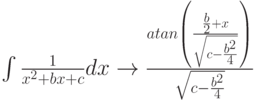
при решении с конкретными значениями – все верно.
![\int \frac{1}{x^2+4x+1}dx \to - \frac {\sqrt{3} atanh \left[ \frac{\sqrt{3}(x+2)}{3} \right] }{3}](/sites/default/files/tex_cache/c95dd1c9c9882cb4bb01cca97f06d985.png) - корни действительные,
- корни действительные,
![\int \frac{1}{x^2+x+1}dx \to - \frac { 2 \sqrt{3} atan \left[ \frac{2 \sqrt{3} \left (x+\frac{1}{2} \right) }{3} \right] }{3}](/sites/default/files/tex_cache/99c6443b64213053cc75d238a56ede41.png) - корни мнимые.
- корни мнимые.
Теперь сложнее:
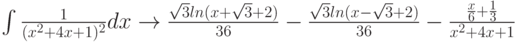
Проверим:

Следующий пример демонстрирует интегрирование тригонометрических функций:
![\int \frac{1}{a+b \cdot sin(x)+c \cdot cos(x)} dx \to \frac{2atan \left[ \frac {b+tan \left( \frac{x}{2} \right) \cdot (a-c)}{\sqrt{a^2-b^2-c^2}} \right]}{\sqrt{a^2-b^2-c^2}}](/sites/default/files/tex_cache/cd285201c9aa3b71adfdff0f9151e83e.png)

Читатель, несомненно, вспомнит достаточно изощренный способ его нахождения, сводящийся к интегрированию по частям и в результате – к получению уравнения относительно самого этого интеграла; решение этого уравнения и дает искомый результат [10].
Среда MathCad также позволяет дифференцировать по параметру определенный интеграл с подынтегральной функцией и пределами интегрирования, зависящими от этого параметра:
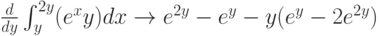
Действия с матрицами охватывают весь стандартный набор операторов алгебры матриц. На панели Symbolic расположены три оператора:  ,
, и
и  для транспонирования, обращения и поиска определителя соответственно. Остальные операторы выполняются при помощи функций (в количестве 47 для MathCad 14) раздела Vector and Matrix меню Insert / Function.
для транспонирования, обращения и поиска определителя соответственно. Остальные операторы выполняются при помощи функций (в количестве 47 для MathCad 14) раздела Vector and Matrix меню Insert / Function.
В качестве примера приведем символьный расчет определителя матрицы 3*3:
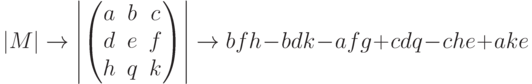
Связь с MS Excel достигается встроенными средствами и специальным расширением MathCad Add – In For Excel. В первом случае легко осуществляется вставка диапазона ячеек из Excel в переменную MathCad при помощи буфера ОС (команды "Копировать/Вставить"). Можно вставить и связать фрагмент таблицы Excel документ MathCad при помощи команды меню "Правка/Специальная вставка". При этом текущие изменения в документе Excel будут сразу же отражаться во вставленном в MathCad фрагменте, откуда их легко вручную можно скопировать в любую переменную MathCad. Но вот связать переменную MathCad с ячейкой Excel, чтобы все изменения выполнялись автоматически, можно только при помощи программного расширения MathCad Add – In For Excel.