Системы компьютерной математики (СКМ)
12.1. История создания СКМ
Первый этап – компьютер, оправдывая свое название (в переводе с англ. "вычислитель"), работал как мощный программируемый калькулятор, способный быстро и автоматически (по веденной программе) выполнять сложные и громоздкие арифметические и логические операции над числами.
Успехи вычислительной математики и постоянно совершенствующиеся численные методы позволяют решить таким способом любую математическую задачу применительно к любой отрасли знаний. Важно отметить, что результат вычислений при этом представляется одним конечным числом в арифметическом виде, то есть при помощи десятичных цифр. Иногда результат представляется множеством (массивом, матрицей) таких чисел, но существо представления от этого не меняется – результат в виде конечного десятичного арифметического числа.
Однако такой результат часто не удовлетворял профессиональных математиков, и вот почему. Подавляющее большинство результатов нетривиальных математических вычислений в классической математике традиционно записывается в символьной форме: с использованием специальных общеизвестных чисел:  ,
,  ,
,  , а иррациональные значения – с помощью радикала. Считается, что в противном случае имеет место принципиальная потеря точности.
, а иррациональные значения – с помощью радикала. Считается, что в противном случае имеет место принципиальная потеря точности.
Другой классический пример, вызывающий замечание математика – выражение, знакомое любому школьнику:

всегда равное единице; а в компьютере либо будет предпринята попытка вычислить это выражение (с неизбежными ошибками округления), либо будет выдано сообщение о неопределенности аргумента Х и всякие дальнейшие действия будут прекращены.
На этом первый этап завершился...
Естественно, вслед за стремительным совершенствованием компьютерных систем человеку в компьютерных расчетах захотелось большего: почему бы не заставить компьютер выполнять преобразования традиционными для математики способами (дробно-рациональные преобразования, подстановки, упрощения, решение уравнений, дифференцирование и т.п.).
Их принято называть преобразованиями в символьном виде или аналитическими преобразованиями, а результат получать не как раньше – в виде одного числа, а в виде формулы.
К этому моменту практически все области человеческой деятельности оказались охваченными каждая своим собственным математическим аппаратом и обзавелись собственными пакетами прикладного программного обеспечения (ППО). При этом всем понадобился универсальный математический инструмент, ориентированный на широкий круг пользователей, которые не являются ни профессионалами в математике, ни программистами, воспитанными на узкоспециальных, малопонятных большинству конечных пользователей компьютерных языках.
Это привело к созданию компьютерных систем символьной математики, рассчитанных на широкие круги пользователей – непрофессионалов в математике. Так началась с середины 60-х годов ХХ века эра систем компьютерной математики (СКМ), по-английски CAS – Сomputer algebra system.
В конце 60-х годов в России на отечественных ЭВМ серии "Мир", разработанных под руководством академика В. Глушкова, была реализована СКМ на языке программирования "Аналитик", обладающая всеми возможностями символьных вычислений, впрочем, с весьма скромными, по нынешним понятиям, характеристиками.
Конечно, даже самые простые неинтеллектуальные компьютерные математические справочники представляют большой практический интерес – ведь ни один самый способный человек не в состоянии вместить в своей голове все математические законы и правила, созданные за многовековую историю человечества.
Данные об особенностях существующих СКМ приведены в табл. 12.1.
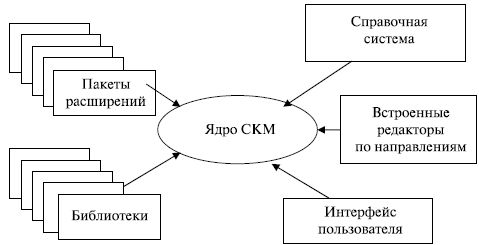
Рассмотрим внутреннюю архитектуру СКМ на примере наиболее мощной, по мнению ряда авторитетных специалистов [6], СКМ Mathematica, обладающей наиболее развитой системой символьной математики. На рис.12.1 представлена ее программная архитектура.
Центральная часть – ядро (Kernel) системы СКМ реализует алгоритм функционирования СКМ, обеспечивает совместное функционирование всех ее частей, организует прием и интеллектуальную обработку запроса пользователя, а затем – вызов нужной процедуры решения. В ядре помещается большое количество встроенных функций и операторов системы. Их количество в современных СКМ может достигать многих тысяч. Например, ядро системы Mathematica 4 содержит данные более чем 5000 одних только интегралов, хотя для интегрирования используются только несколько встроенных функций.
Поиск и выполнение функций и процедур, встроенных в ядро СКМ, выполняется быстро, если их там не слишком много. Поэтому объем ядра ограничивают, но к нему добавляют встроенные в СКМ библиотеки процедур и функций, использующихся относительно редко. При этом общее число доступных пользователю математических функций ядра и этих встроенных библиотек достигает многих тысяч.
Кардинальное расширение возможностей СКМ и их приспособленность к нуждам конкретных пользователей для углубленного решения определенного круга задач (например, задач теоретической и прикладной статистики, векторного анализа) достигается за счет установки внешних пакетов расширения. Эти пакеты, приобретаемые отдельно, делают возможности СКМ практически безграничными.
Все эти библиотеки, пакеты расширений и справочная система современных СКМ (назовем их инструментами СКМ) содержат не только и не просто знания в области математики, накопленные за много веков ее развития (этим никого не удивишь: именно такие возможности характерны для широко распространенного класса ИПО – информационно-поисковых систем). Но восхищает, что эти инструменты удивительным образом автоматически и творчески используют такие знания для решения задач, где нужно выбрать и уметь применить один, единственный из многих десятков, неочевидный метод решения. Например, СКМ могут мгновенно найти неопределенный интеграл либо сразу же сообщить о невозможности его представления элементарными функциями – задача непростая, даже для профессионального математика. Не менее впечатляет и то, что если после получения искомой формулы перейти к началу документа и задать входящим в эту формулу параметрам конкретные числовые значения, мгновенно будет получен ее численный результат. В состав любой СКМ входит набор редакторов (на рис.12.1 они названы редакторами по направлениям): текстовый, формульный, графический редакторы, средства поддержки работы в сети и HTML(XML)-средства, пакеты анимации и аудиосредства.
Благодаря всем этим возможностям СКМ могут быть отнесены к программным продуктам самого высокого на сегодняшний день уровня – интеллектуального. Такие программы в настоящее время объединяются термином "базы знаний". Современные СКМ, по мнению признанных авторитетов [6, 7], предоставляет неискушенному пользователю возможности выпускника математического вуза в областях численных методов расчета, математического анализа, теории матриц и других общих разделах высшей математики, позволяющих получить конструктивные результаты.
Конечно, в абстрактных разделах математики, типа функционального анализа или вопросов "существования и единственности..." СКМ пока вряд ли могут быть полезны (кроме как для предоставления нужной справки, что очень даже немало), но в прикладных задачах, для которых СКМ и создавались, такие разделы математики обычно не задействованы.
12.2. Интегрированная Среда СКМ MathCad
Интегрированная Среда СКМ MathCad является системой СКМ универсального назначения и наиболее приспособлена для решения широкого спектра, а точнее –практически любых математических задач, в основном непрофессиональными математиками, а также для эффективного использования во всех областях сферы образования.
По сей день они остаются единственными математическими системами, в которых описание решения математических задач дается с помощью привычных математических формул и знакомых символов. Такой же вид имеют и результаты вычислений. СКМ MathCad не очень подходит для серьезной профессиональной научной деятельности математиков, она больше предназначена для решения не слишком изощренных математических задач, выполнения технических расчетов любой сложности, а главное – не имеет конкурентов в области образования. Благодаря высоким характеристикам, СКМ MathCad полностью оправдывает термин "CAD" в своем названии (Computer Aided Design), подтверждающий принадлежность к классу наиболее сложных и совершенных систем автоматического проектирования – САПР. Система MathCad является типичной интегрированной системой, то есть объединяющей в своем составе несколько обособленных программных средств для решения определенного круга самостоятельных задач.. Первоначально она была предназначена для сугубо численных вычислений и ориентирована под MS-DOS, но, начиная с версии 3.0 (1990 г.), работает под ОС Windows и имеет достаточно широкий набор средств для символьных и графических вычислений.
Все действия в СКМ MathCad сразу оформляются в виде документа, состоящего из рабочих листов, на которых помещается описание алгоритма, рабочие формулы, комментарии, иллюстрации, графики, таблицы. Форма такого документа максимально приспособлена для печати, передачи по сети Internet и не требует дополнительного редактирования. С другой стороны, этот документ, имеющий расширение .mcd, содержит в скрытом виде всю программу вычислений. Он может быть импортирован как для целей издания, так и для продолжения и совершенствования программных вычислений. Весь документ или отдельные его части могут быть заблокированы для редактирования путем задания пароля.
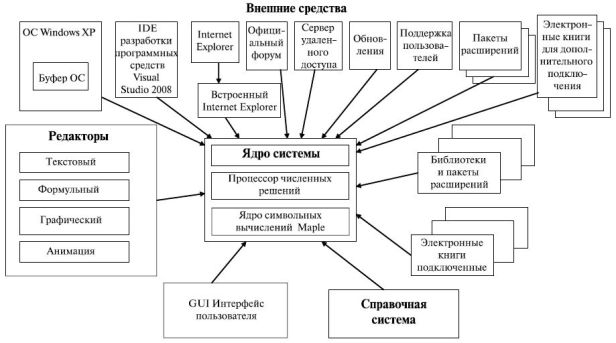
На рис.12.2 приведена архитектура СКМ MathCad. Центральным блоком являются два ядра: собственно ядро СКМ и ядро символьных вычислений, аналогичное СКМ Maple, приобретенное у разработчика – фирмы Waterloo Maple.
Встроенные в среду MathCad электронные книги (e-Books) содержат примеры, справки и типовые расчеты из различных областей науки, техники, экономики. Любой фрагмент из этих книг можно скопировать на рабочий лист документа и выполнить.
Библиотеки и пакеты расширений, ориентированные на решение различных прикладных задач, поставляются и устанавливаются разработчиком отдельно.
Мощный интерфейс СКМ MathCad не требует программирования при вводе заданий и индикации результатов – все это выполняется в традиционной форме на общепринятом языке математических символов и формул без применения каких-либо специальных команд или операторов. Показательно, что в каждом алгоритмическом языке простое возведение в степень, в меру фантазий разработчиков языка, выполняется при помощи уникальных собственных условных обозначений – всевозможных стрелочек, крышечек, двойных звездочек и Бог знает чего еще, а то и вовсе отсутствует и требует вызова специальных функций – как в языках семейства Си. В MathCad эта операция имеет привычный вид.
Интерфейс является визуальным – то есть практически любые действия в СКМ можно выполнять без помощи клавиатуры, просто выбирая нужные пункты меню или инструменты на панелях. В этом интерфейсе реализован принцип "WYSIWYG" – что видим на экране, то и получаем в работе и при выводе.
Интерфейс интеллектуален – конечно, здесь далеко до интеллекта Visual Studio-2010, но во многих случаях он не допустит ошибочных действий пользователя.
Упомянутый входной язык ввода является интерпретирующим, то есть промежуточные результаты появляются по мере ввода очередной формулы. Сама же СКМ MathCad написана на одном из самых мощных языков – С++. По мере того, как пользователь набирает на рабочем листе текст алгоритма вычислений, среда сама составляет скрытую программу на промежуточном языке связи, которая затем сохраняется в виде файла с расширением .mcd. К сожалению, исполняемого файла с расширением .ехе пакет MathCad не формирует – для работы с импортированным документом необходимо наличие установленного приложения MathCad. А вот вставить образ документа либо отдельный его фрагмент в текстовый редактор, например, MS WORD, через системный буфер никакого труда не представляет. Именно так и вставлялись все иллюстрации в этой главе. Рекомендую после такой вставки фрагмента вызвать на нем контекстное меню – пункт "Формат рисунка…/Размер" и установить в окне "Масштаб по высоте" 128% – для шрифта 12-го кегля наиболее подходящий.
Объектами рабочего листа могут быть формульные текстовые или графические блоки. Действия над блоками выполняются в строгом порядке слева направо, сверху вниз. Блоки, готовящие операции, должны предшествовать выполнению этих операций. При этом организована сквозная передача данных от одного объекта к другому. Изменение входных данных мгновенно обеспечивает пересчет результатов.
Контент (содержание) этой СКМ можно рассматривать в качестве исключительно мощного справочного средства по математике. Кроме того, в СКМ MathCad интегрированы формульный, текстовый и графический редакторы, позволяющие упростить ввод многоэтажных сложнейших формул и получить итоговый документ. Промежуточные действия в ходе символьных преобразований в СКМ MathCad скрыты от пользователя, но не следует забывать, что для получения конечного результата используются сложнейшие рекурсивные алгоритмы, мало знакомые широкому пользователю и зачастую не оптимальные на взгляд математика. При этом никто не запрещает пользователю пошаговое выполнение и индикацию знакомых из литературы алгоритмов, что значительно упрощает решение при известном конечном результате. В СКМ MathCad не создается итоговый исполняемый *.exe файл, значит, для просмотра готового (например, импортированного) документа требуется наличие установленного пакета СКМ MathCad.
Перечислим основные возможности Среды MathCad.
Общие возможности
- Разработка и редактирование документов, содержащих как математические формулы любой сложности, так и все встроенные инструменты Среды MathCad. Подготовка этих документов к изданию или передаче по сети Internet.
- Использование общепринятого расширяемого языка разметки XML как универсального способа организации обмена данными с другими приложениями. Это позволяет преобразовывать файлы MathCad в HTML-страницы и в формат PDF.
- Возможность вставки в документ широкого спектра объектов (см. рис.12.3.)
- Разработка веб-документов и сетевые возможности по их пересылке, получению обновлений и поддержки.
- Получение документов MathCad по сети и выполнение расчетов в этих документах.
- Получение через Internet и подключение новых книг расширения для реализации дополнительных возможностей среды MathCad.
- Доступный официальный форум.
- Использование серверных услуг среды MathCad (Mathcad Application Server) – удаленное подключение к пакету MathCad в полной комплектации через стандартный веб-браузер Internet, даже если MathCad не установлен на компьютере.
- Импорт документов из MS Access и MS Excel и математическая обработка данных из этих документов.
- Наличие обширных справочных материалов по математике и основных физических констант, а также большое количество задач с готовыми решениями по многим разделам науки и техники.
- Выполнение вычислений любой сложности – использование среды MathCad в качестве сверхмощного научного интеллектуального калькулятора с применением богатой библиотеки встроенных функций ( более 680; для сравнения, в MS Excel их около 200), с точностью до 17 значащих цифр (а при использовании специальных операторов – и до 250) и с неограниченными возможностями запоминания промежуточных результатов. При этом имеется возможность вычислений как по введенной в документ формуле целиком, так и по отдельному, выделенному фрагменту формулы.
- Использование графического редактора для построения двумерных и трехмерных графиков любой сложности, наглядных диаграмм и не только для простого построения, но и для связи графика с формулой, при которой изменение параметра сразу отражается на кривой графика. Имеется также возможность создание объектов движущейся анимации и просмотра импортированных файлов, например, видеофильмов в формате AVI при помощи встроенного в среду MathCad проигрывателя Playback.
- Действия с размерностями.
Численные методы вычислений
- Решение уравнений и систем уравнений, как линейных, так и нелинейных. Нахождение корней многочлена.
- Решение неравенств.
- Вычисление определенного интеграла.
- Вычисление несобственных интегралов.
- Вычисление кратных интегралов.
- Численные методы дифференцирования.
- Численное решение обыкновенных дифференциальных уравнений – задача Коши.
- Численное решение обыкновенных дифференциальных уравнений – решение краевой задачи.
- Решение дифференциальных уравнений в частных производных.
- Вычисление суммы и произведения членов ряда.
- Исследование функций и численное определение экстремумов функций одной и нескольких переменных, построение асимптот.
- Решение оптимизационной задачи методом линейного программирования.
Символьные вычисления
- Выполнение точных вычислений с представлением результатов в традиционной математической форме – с записью ответа в форме радикала и специальных иррациональных чисел
 ,
,  ,
,  .
. - Символьные преобразования математических выражений целиком или их фрагментов:
- разложение выражений в более простые;
- приведение подобных;
- разложение на множители;
- приведение к общему знаменателю;
- вынесение общего множителя;
- разложение на элементарные дроби;
- вычисление коэффициентов полиномов;
- выполнение подстановок.
- Аналитическое решение уравнений и систем уравнений.
- Дифференцирование в символьной форме определение производных любых порядков.
- Аналитическое определение первообразной.
- Построение касательной и нормали к плоской кривой и к поверхности.
- Аналитическое вычисление определенного интеграла.
- Символьное вычисление кратных интегралов.
- Решение неравенств.
- Аналитическое вычисление предела.
- Аналитическое вычисление суммы ряда конечного или бесконечного.
- Аналитическое вычисление произведения членов ряда конечного или бесконечного.
- Аналитическое вычисление суммы/произведения членов ряда конечного или бесконечного, когда пределы и шаг изменения индекса члена ряда задаются (например, сложить четные числа от
 до
до 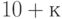 .)
.) - Разложение в ряд Тейлора.
- Разложение в ряд Фурье.
- Символьное преобразование Фурье и Лапласа – прямое и обратное.
- Операции с матрицами в символьной форме: умножение и сложение матриц, поиск обратной матрицы, вычисление определителя, поиск собственных значений и собственных векторов.
Работа с матрицами и матричные вычисления
- Элементарные матричные действия: создание, импорт, заполнение матриц, задание матриц специального вида, умножение, сложение, транспонирование и сортировка матрицы в целом или ее фрагмента. Выполнение векторизации – однотипных действий над всеми элементами матрицы.
- Вычисление определителя, размерности, ранга и следа матрицы, скалярное и векторное умножение векторов, вычисление якобиана, например, для перехода к другим системам координат в тройном интеграле. Вычисление собственных значений и собственных векторов, поиск максимального и минимального элемента матрицы.
- Матричные преобразования: скалярное и векторное умножение векторов, поиск обратной матрицы и решение системы алгебраических линейных уравнений, всевозможные разложения матрицы на произведение матриц специального вида: двух треугольных – верхней и нижней (LU-преобразование), треугольной и ее же транспонированной (разложение Холецкого), ортогональной и верхней треугольной (QR-разложение), сингулярное разложение.
- Интегрирование среды MathCad с матричной математической системой MATLAB и возможность использования ее аппарата открывает удивительные возможности эффективного решения матричных задач неограниченной сложности.
Решение дифференциальных уравнений
Программирование
Составление программ и выполнение расчетов на упрощенном процедурном алгоритмическом языке с возможностью использования всех процедурных конструкций: условных операторов, циклов, массивов, модуль-функций, модуль-процедур.
Комплексные числа
- Представление комплексных чисел в традиционной форме, возможность выполнения основных арифметических действия с ними.
- Возможность автоматического получения результатов многих вычислений в виде комплексного числа (например, всех корней многочлена).
- Возможность задания комплексного аргумента для многих библиотечных функций и получение математически корректного результата.
Обработка данных и финансовые расчеты
Теория вероятностей и математическая статистика
Математическое моделирование
Специальные возможности по прикладным инженерным и научным расчетам
- Обработка электрических сигналов и расчет электронных устройств.
- Виртуальная генерация электрических сигналов и их обработка.