Графы: представления, достижимость и связность

Взаимная достижимость, компоненты сильной связности и базы графа

По аналогии с графом достижимости определим граф сильной достижимости.

Определение 9.10. Пусть G=(V,E) - ориентированный граф. Граф сильной достижимости G_*^*=(V,E_*^*) для G имеет то же множество вершин V и следующее множество ребер E_*^* ={ (u, v) | в графе G вершины v и u взаимно достижимы}.

По матрице графа достижимости 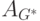легко построить матрицу 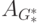графа сильной достижимости. Действительно из определений достижимости и сильной достижимости непосредственно следует, то для всех пар (i,j), 1<= i,j <= n, значение элемента 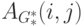равно 1 тогда и только тогда, когда оба элемента A_G*(i, j) и A_G*(j, i) равны 1, т.е.

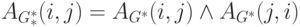
По матрице 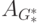можно выделить компоненты сильной связности графа G следующим образом.

1. Поместим в компоненту K₁ вершину v₁ и все такие вершины v_j, что A_{G_*^*}(1,j) = 1.
2. Пусть уже построены компоненты K₁, ..., K_i и v_k - это вершина с минимальным номером, еще не попавшая в компоненты. Тогда поместим в компоненту K_{i+1} вершину v_k и все такие вершины v_j,
3. что A_{G_*^*}(k,j) = 1.

Повторяем шаг (2) до тех пор, пока все вершины не будут распределены по компонентам.

В нашем примере для графа G на рис.2 по матрице 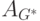получаем следующую матрицу графа сильной достижимости

Используя описанную выше процедуру, находим, что вершины графа G разбиваются на 4 компоненты сильной связности: K₁= {v₁, v₂, v₃}, \ K₂ ={ v₄}, \ K₃ ={ v₅}, \ K₄ ={ v₆}. На множестве компонент сильной связности также определим отношение достижимости.

Определение 9.11. Пусть K и K' - компоненты сильной связности графа G. Компонента K достижима из компоненты K^\prime, если K= K' или существуют такие две вершины 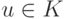и 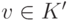, что u достижима из v. K строго достижима из K^\prime, если и K достижима из K'. Компонента K называется минимальной, если она не является строго достижимой ни из какой компоненты.

Так как все вершины в одной компоненте взаимно достижимы, то нетрудно понять, что отношения достижимости и строгой достижимости на компонентах не зависят от выбора вершин 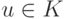и .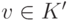

Из определения легко выводится следующая характеристика строгой достижимости.

Лемма 9.3. Отношение строгой достижимости является отношением частичного порядка, т.е. оно антирефлексивно, антисимметрично и транзитивно.

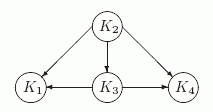
Это отношение можно представлять в виде ориентированного графа, вершинам и которого являются компоненты, а ребро (K', K) означает, что K строго достижима из K'. На рис. 9.4 показан этот граф компонент для рассматриваемого выше графа G.

Рис. 9.4. Граф отношения достижимости на компонентах G

В данном случае имеется одна минимальная компонента K₂.

Во многих приложениях ориентированный граф представляет собой сеть распространения некоторого ресурса: продукта, товара, информации и т.п. В таких случаях естественно возникает задача поиска минимального числа таких точек (вершин), из которых этот ресурс может быть доставлен в любую точку сети.

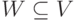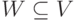Определение 9.12. Пусть G=(V,E) - ориентированный граф. Подмножество вершин называется порождающим, если из вершин W можно достичь любую вершину графа. Подмножество вершин называется базой графа, если оно является порождающим, но никакое его собственное подмножество порождающим не является.

Следующая теорема позволяет эффективно находить все базы графа.

Теорема 9.1. Пусть G=(V,E) - ориентированный граф. Подмножество вершин 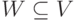является базой G тогда и только тогда, когда содержит по одной вершине из каждой минимальной компоненты сильной связности G и не содержит никаких других вершин.

Доказательство Заметим вначале, что каждая вершина графа достижима из вершины, принадлежащей некоторой минимальной компоненте. Поэтому множество вершин W, содержащих по одной вершине из каждой минимальной компоненты, является порождающим а при удалении из него любой вершины перестает быть таковым, так как вершины из соответствующей минимальной компоненты становятся недостижимы. Поэтому W является базой.

Обратно, если W является базой, то оно обязано включать хотя бы по одной вершине из каждой минимальной компоненты, иначе вершины такой минимальной компоненты окажутся недоступны. Никаких других вершин W содержать не может, так как каждая из них достижима из уже включенных вершин.

Из этой теоремы вытекает следующая процедура построения одной или перечисления всех баз графа G.

1. Найти все компоненты сильной связности G.
2. Определить порядок на них и выделить минимальные относительно этого порядка компоненты.
3. Породить одну или все базы графа, выбирая по одной вершине из каждой минимальной компоненты.

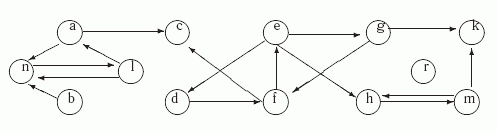
Пример 9.5. Определим все базы ориентированного графа G, показанного на рис.9.5.

Рис. 9.5. Граф G

На первом этапе находим компоненты сильной связности G:

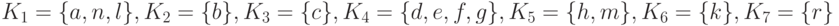
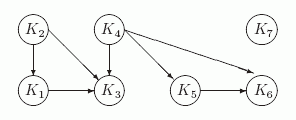
На втором этапе строим граф строгой достижимости на этих компонентах.

Рис. 9.6. Граф отношения достижимости на компонентах G

Определяем минимальные компоненты: K₂ = { b }, K₄ ={ d,e, f, g} и K₇= { r}.

Наконец перечисляем все четыре базы G: B₁= { b, d, r}, B₂= { b, e, r}, B₃= { b, f, r} и B₁= { b, g, r}.

Задачи

Задача 9.1. Докажите, что сумма степеней всех вершин произвольного ориентированного графа четна.

У этой задачи имеется популярная интерпретация: доказать, что общее число рукопожатий, которыми обменялись люди, пришедшие на вечеринку, всегда четно.

Задача 9.2. Перечислите все неизоморфные неориентированные графы, у которых не более четырех вершин.

Задача 9.3. Докажите, что неориентированный связный граф остается связным после удаления некоторого ребра 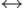это ребро принадлежит некоторому циклу.

Задача 9.4. Докажите, что неориентированный связный граф с n вершинам и

• содержит не менее n-1 ребер,
• если содержит больше n-1 ребер, то имеет, по крайней мере, хотя бы один цикл.

Задача 9.5. Докажите, что в любой группе из 6 человек есть трое попарно знакомых или трое попарно незнакомых.

Задача 9.6. Докажите, что неориентированный граф G=(V,E) связен 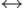для каждого разбиения с непустыми V₁ и V₂ существует ребро, соединяющее V₁ с V₂.

Задача 9.7. Докажите, что, если в неориентированном графе имеется ровно две вершины нечетной степени, то они связаны путем.

Задача 9.8. Пусть G=(V,E) неориентированный граф с |E| < |V|-1. Докажите, что тогда G несвязный граф.

Задача 9.9. Докажите, что в связном неориентированном графе любые два простых пути максимальной длины имеют общую вершину.

Задача 9.10. Пусть неориентированный граф без петель G=(V,E) имеет k компонент связности. Доказать, что тогда

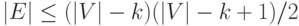
Задача 9.11. Определите, что представляет из себя граф достижимости для

• графа с n вершинам и и пустым множеством ребер;

• графа с n вершинам и: V= {v₁,... , v_n}, ребра которого образуют цикл:

  

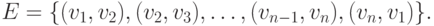
Задача 9.12. Вычислите матрицу графа достижимости 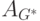для графа

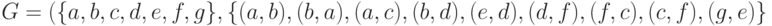
и постройте соответствующий ей граф достижимости. Найдите все базы графа G.

Задача 9.13. Построить для заданного на рис. 9.7 ориентированного графа G₁=(V,E) его матрицу смежности A_G1, матрицу инцидентности B_G1 и списки смежности. Вычислить матрицу достижимости A_G1* и построить соответствующий граф достижимости G₁^*.

Рис. 9.7.