|
Это в лекции 3. |
Графы: представления, достижимость и связность
Граф достижимости
Один из первых вопросов, возникающих при изучении графов, это вопрос о существовании путей между заданными или всеми парами вершин. Ответом на этот вопроc - введенное выше отношение достижимости на вершинах графа G=(V,E): вершина w достижима из вершины v, если v = w или в G есть путь из v в w. Иначе говоря, отношение достижимости является рефлексивным и транзитивным замыканием отношения E. Для неориентированных графов это отношение также симметрично и, следовательно, является отношением эквивалентности на множестве вершин V. В неориентированном графе классы эквивалентности по отношению достижимости называются связными компонентами. Для ориентированных графов достижимость, вообще говоря, не должна быть симметричным отношением. Симметричной является взаимная достижимость.
Определение 9.8. Вершины v и w ориентированного графа G=(V,E) называются взаимно достижимыми, если в G есть путь из v в w и путь из w в v.
Ясно, что отношение взаимной достижимости является рефлексивным, симметричным и транзитивным и, следовательно, эквивалентностью на множестве вершин графа. Классы эквивалентности по отношению взаимной достижимости называются компонентами сильной связности или двусвязными компонентами графа.
Рассмотрим вначале вопрос о построении отношения достижимости. Определим для каждого графа его граф достижимости ( называемый иногда также графом транзитивного замыкания), ребра которого соответствуют путям исходного графа.
Определение 9.9. Пусть G=(V,E) - ориентированный граф. Граф достижимости G*=(V,E*) для G имеет то же множество вершин V и следующее множество ребер E* ={ (u, v) | в графе G вершина v достижима из вершины u}.
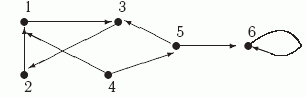
Пример 9.3. Рассмотрим граф G из примера 9.2.
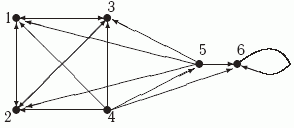
Тогда можно проверить, что граф достижимости G* для G выглядит так (новые ребра -петли при каждой из вершин 1-5 не показаны):
Каким образом по графу G можно построить граф G*? Один способ заключается в том, чтобы для каждой вершины графа G определить множество достижимых из нее вершин, последовательно добавляя в него вершины, достижимые из нее путям и длины 0, 1, 2 и т.д.
Мы рассмотрим другой способ, основанный на использовании матрицы смежности AG графа G и булевых операций. Пусть множество вершин V={v1, ... , vn}. Тогда матрица AG - это булева матрица размера n x n.
Ниже для сохранения сходства с обычными операциями над матрицами
мы будем использовать "арифметические" обозначения для
булевых операций: через + будем обозначать дизъюнкцию 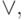 а через x - конъюнкцию
а через x - конъюнкцию 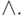
Обозначим через En единичную матрицу размера n x n.
Положим 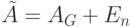 .
Пусть
.
Пусть 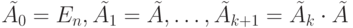 .
Наша процедура построения G* основана на следующем утверждении.
.
Наша процедура построения G* основана на следующем утверждении.
Лемма 9.2.
Пусть  . Тогда
. Тогда
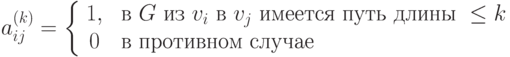
Доказательство проведем индукцией по k.
Базис. При k=0 и k=1 утверждение справедливо по определению 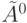 и
и 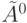 .
.
Индукционный шаг. Пусть лемма справедлива для k. Покажем, что она
остается справедливой и для k+1. По определению 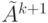 имеем:
имеем:
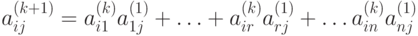
Предположим, что в графе G из vi в vj имеется путь длины <= k+1. Рассмотрим кратчайший из таких путей.
Если его длина <= k, то по предположению индукции a_{ij}^{(k)}=1. Кроме того, ajj(1)=1. Поэтому aij(k) ajj(1)=1 и aij(k+1)=1.
Если длина кратчайшего пути из из vi в vj равна k+1, то пусть vr - его предпоследняя вершина. Тогда из vi в vr имеется путь длины k и по предположению индукции air(k)=1. Так как 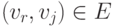 , то a_{rj}^{(1)}=1. Поэтому air(k) arj(1)=1 и aij(k+1)=1.
, то a_{rj}^{(1)}=1. Поэтому air(k) arj(1)=1 и aij(k+1)=1.
Обратно, если aij(k+1)=1, то хотя бы для одного r слагаемое air(k) arj(1) в сумме равно 1. Если это r=j, то aij(k)=1 и по индуктивному предположению в G имеется путь
из vi в vj длины <= k. Если же 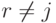 , то air(k)=1 и arj(1)=1. Это означает, что в G имеется путь
из vi в vr длины <= k и ребро
, то air(k)=1 и arj(1)=1. Это означает, что в G имеется путь
из vi в vr длины <= k и ребро 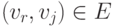 . Объединив их,
получаем путь из vi в vj длины <= k+1.
. Объединив их,
получаем путь из vi в vj длины <= k+1.
Из лемм 9.1 и 9.2 непосредственно получаем
Следствие 1. Пусть G=(V,E) - ориентированный граф с n вершинам и, а G* - его граф достижимости. Тогда A_{G*} = 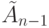 . Доказательство. Из леммы 5.1 следует, что, если в G
имеется путь из u в
. Доказательство. Из леммы 5.1 следует, что, если в G
имеется путь из u в 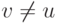 , то в нем имеется и простой путь из u в v
длины <= n-1. А по лемме 5.2 все такие пути представлены в матрице
, то в нем имеется и простой путь из u в v
длины <= n-1. А по лемме 5.2 все такие пути представлены в матрице 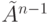 .
.
Таким образом процедура построения матрицы смежности AG* графа достижимости для G сводится к возведению матрицы 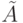 в степень n-1. Сделаем несколько замечаний, позволяющих упростить эту процедуру.
в степень n-1. Сделаем несколько замечаний, позволяющих упростить эту процедуру.
-
Для возведения матрицы
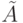 в произвольную степень n достаточно выполнить
в произвольную степень n достаточно выполнить ![]\log_2 n[](/sites/default/files/tex_cache/27f6154d445e47a92efd112c918f7fd3.png) возведений в квадрат:где k - это наименьшее число такое, что 2k >= n.
возведений в квадрат:где k - это наименьшее число такое, что 2k >= n.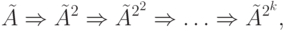
- Так как на диагонали в матрице
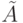 стоят единицы, то для любых i < j все единицы матрицы
стоят единицы, то для любых i < j все единицы матрицы 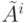 сохраняются в матрице
сохраняются в матрице 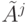 , в частности, и в матрице
, в частности, и в матрице 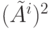 .
. -
Если при вычислении элемента aij(2) матрицы
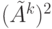 по стандартной формуле
по стандартной формуле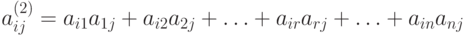
обнаруживается такое r, что air = 1 и arj =1, то и вся сумма aij(2) =1. Поэтому остальные слагаемые можно не рассматривать.
Пример 9.3. Рассмотрим в качестве примера вычисление матрицы графа достижимости AG* для графа G, представленного на рис.9.2. В этом случае
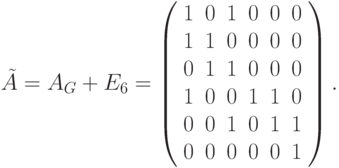
Так как у G имеется 6 вершин, то 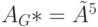 . Вычислим эту матрицу:
. Вычислим эту матрицу:
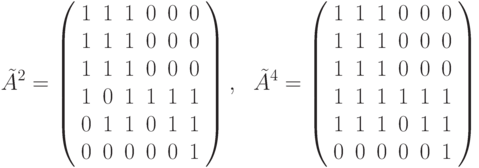
и  (последнее равенство нетрудно проверить).
Таким образом,
(последнее равенство нетрудно проверить).
Таким образом,
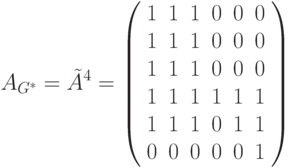
Как видим, эта матрица действительно задает граф 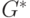 , представленный на рис.9.3.
, представленный на рис.9.3.