НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 14: Характеристические функции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 07.04.2008 | Уровень: специалист | Доступ: платный | ВУЗ: Новосибирский Государственный Университет

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать программу

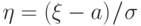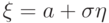Пример 78. Вычислим характеристическую функцию случайной величины $\xi$ , имеющей нормальное распределение с параметрами и $\sigma^2$ . Мы знаем, что у "стандартизованной" случайной величины, $\eta=(\xi-a)\mspace{1mu}/\mspace{1mu}\sigma$ характеристическая функция равна $\phi_\eta(t)=e^{-t^2/2}$ . Тогда характеристическая функция величины $\xi=a+\sigma\eta$ равна

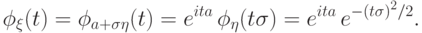
$\phi_\xi(t)=\phi_{a+\sigma\eta}(t)=e^{ita}\,\phi_\eta(t\sigma)= e^{ita}\,e^{-{(t\sigma)}^2/2}.$

(Ф4). Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины $\xi$ и $\eta$ независимы, то, по свойству (E7) математических ожиданий,

$\phi_{\xi+\eta}(t)={\mathsf E\,} e^{it(\xi+\eta)}= {\mathsf E\,} e^{it\xi}\,{\mathsf E\,} e^{it\eta}= \phi_\xi(t)\,\phi_\eta(t).$

Замечание Чтобы характеристическая функция суммы

случайных величин распадалась в произведение их характеристических функций, попарной независимости слагаемых не хватит. То же самое можно сказать про свойство (E7) математических ожиданий. Если же сомножители независимы в совокупности, то их совместное распределение распадается в произведение распределений, и тогда математическое ожидание произведения распадается в произведение математических ожиданий.

Замечательным свойством (Ф4) мы сразу же воспользуемся, как обещали, для доказательства леммы 3, утверждающей устойчивость нормального распределения относительно суммирования.

Доказательство леммы 3. Пусть $\xi{\,\sim\,}{\mathrm N}_{a_1,\,\sigma_1^2}$ и $\eta{\,\sim\,}{\mathrm N}_{a_2,\,\sigma_2^2}$ независимы. Характеристическая функция суммы $\xi+\eta$ равна

$\phi_{\xi+\eta}(t)=\phi_\xi(t)\,\phi_\eta(t)= {e\vphantom{\sum\limits}}^{ita_1}{e\vphantom{\sum\limits}}^{-{t^2\sigma_1^2}\mspace{1mu}/\mspace{2mu}{2}} {e\vphantom{\sum\limits}}^{ita_2}{e\vphantom{\sum\limits}}^{-{t^2\sigma_2^2}\mspace{1mu}/\mspace{2mu}{2}} = {e\vphantom{\sum\limits}}^{it(a_1+a_2)}{e\vphantom{\sum\limits}}^{-t^2(\sigma_1^2+\sigma_2^2)/\mspace{1mu}2}.$

Видим, что характеристическая функция суммы есть характеристическая функция нормального распределения с параметрами a_1+a_2

и $\sigma_1^2+\sigma_2^2$ . Следовательно, $\xi+\eta {\,\sim\,}{\mathrm N}_{a_1+a_2,\,\sigma_1^2+\sigma_2^2}$ по свойству (Ф2).

Доказательство лемм 1, 2, 4. Докажем свойства устойчивости по суммированию биномиального распределения, распределения Пуассона и гамма-распределения, используя характеристические функции из примеров 73-76.

Для независимых случайных величин с распределениями Пуассона 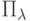$\Pi_\lambda$ и $\Pi_\mu$ характеристическая функция суммы

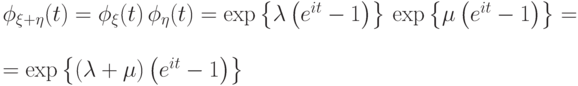
$\phi_{\xi+\eta}(t)= \phi_\xi(t)\,\phi_\eta(t)= \exp\left\{\lambda\left(e^{it}-1\right)\right\} \,\exp\left\{\mu\left(e^{it}-1\right)\right\}=\\= \exp\left\{(\lambda+\mu)\left(e^{it}-1\right)\right\}$

равна характеристической функции распределения Пуассона с параметром $\Pi_{\lambda+\mu}$ .

Для независимых случайных величин с биномиальными распределениями ${\mathrm B}_{n,p}$ и ${\mathrm B}_{m,p}$ характеристическая функция суммы

$\phi_{\xi+\eta}(t)= \phi_\xi(t)\,\phi_\eta(t)= {\left(1-p + pe^{it}\right)}^n\, {\left(1-p + pe^{it}\right)}^m=\\= {\left(1-p + pe^{it}\right)}^{n+m}$

равна характеристической функции биномиального распределения с параметрами n+m

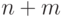и

.

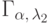Для независимых случайных величин с гамма-распределениями $\Gamma_{\alpha,\,\lambda_1}$ и $\Gamma_{\alpha,\,\lambda_2}$ характеристическая функция суммы

${\vphantom{\textstyle\int}\phi}_{\xi+\eta}(t)= {\left(1-\frac{it}{\alpha}\right)}^{-\lambda_1}{\left(1-\frac{it}{\alpha}\right)}^{-\lambda_2} ={\left(1-\frac{it}{\alpha}\right)}^{-(\lambda_1+\lambda_2)}$

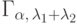равна характеристической функции гамма-распределения $\Gamma_{\alpha,\,\lambda_1+\lambda_2}$ .

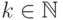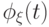(Ф5.) Пусть существует момент порядка $k\in \mathbb N$ случайной величины $\xi$ , т.е. ${\mathsf E\,}|\xi|^k<\infty$ . Тогда характеристическая функция $\phi_\xi(t)$ непрерывно дифференцируема раз и ее -я производная в нуле связана с моментом порядка равенством

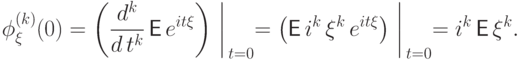
$\phi_\xi^{(k)}(0)=\left(\frac{d^k}{d\,t^k}\,{\mathsf E\,} e^{it\xi}\right) \biggm|_{\,t=0}=\left({\mathsf E\,} i^k\,\xi^k\,e^{it\xi}\right) \biggm|_{\,t=0}=i^k \,{\mathsf E\,}\xi^k.$

Существование и непрерывность -й производной, равно как и законность переноса производной под знак математического ожидания, мы доказывать не будем.

Упражнение. Доказать, что для случайной величины $\xi$ со стандартным нормальным распределением момент четного порядка 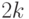равен

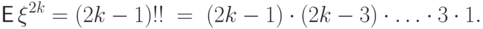
${\mathsf E\,}\xi^{2k}=(2k-1)!! \; = \; (2k-1)\cdot(2k-3)\cdot\ldots\cdot 3\cdot 1.$

Доказать по определению, что все моменты нечетных порядков стандартного нормального распределения существуют и равны нулю.

Как только появились производные высших порядков, самое время разложить функцию в ряд Тейлора.

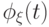(Ф6). Пусть существует момент порядка $k\in\mathbb N$ случайной величины $\xi$ , т.е. ${\mathsf E\,}|\xi|^k<\infty$ . Тогда характеристическая функция $\phi_\xi(t)$ в окрестности точки 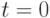t=0 разлагается в ряд Тейлора

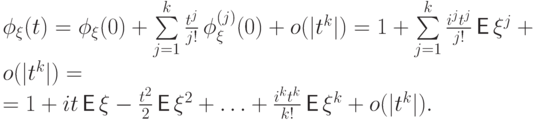
$\phi_\xi(t)&=&\phi_\xi(0)+ \sum\limits_{j=1}^k \frac{t^j}{j!}\,\phi_\xi^{(j)}(0)+o(|t^k|)= 1+\sum\limits_{j=1}^k \frac{i^jt^j}{j!}\,{\mathsf E\,}\xi^j+o(|t^k|)=\\ &=&1+it\,{\mathsf E\,}\xi-\frac{t^2}{2}\,{\mathsf E\,}\xi^2+\ldots+ \frac{i^kt^k}{k!}\,{\mathsf E\,}\xi^k+o(|t^k|).$

Ряды Тейлора бывают особенно полезны в теории пределов. Следующее основное свойство характеристических функций потребуется нам для доказательства предельных теорем, и это свойство - последняя теорема, оставленная нами без доказательства.

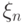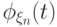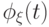Теорема 43 (теорема Леви о непрерывном соответствии). Случайные величины $\xi_n$ слабо сходятся к случайной величине $\xi$ тогда и только тогда, когда для любого характеристические функции $\phi_{\xi_n}(t)$ сходятся к характеристической функции $\phi_\xi(t)$ .

Сформулированная теорема устанавливает непрерывное соответствие между классами 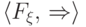$\langle F_\xi,\, \Rightarrow \rangle$ функций распределения со слабой сходимостью и $\langle \phi_\xi,\, \to \rangle$ характеристических функций со сходимостью в каждой точке. "Непрерывность" этого соответствия - в том, что пределу в одном классе относительно заданной в этом классе сходимости соответствует предел в другом классе относительно сходимости, заданной в этом другом классе.

Осталось воспользоваться теоремой о непрерывном соответствии и доказать ЗБЧ в форме Хинчина и ЦПТ.

Дальше >>

Введение в теорию вероятностей

Введение в теорию вероятностей

Лекция 14: Характеристические функции

Вопросы и ответы

Студенты

Авторизоваться

Введение в теорию вероятностей

Введение в теорию вероятностей

Лекция 14: Характеристические функции

Вопросы и ответы

Студенты