НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 10: Числовые характеристики распределений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 07.04.2008 | Уровень: специалист | Доступ: платный | ВУЗ: Новосибирский Государственный Университет

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать программу

Дисперсия и моменты старших порядков

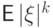Определение 37. Пусть ${\mathsf E\,}|\xi|^k<\infty$ . Число ${\mathsf E\,}\xi^k$ называется моментом порядка или -м моментом случайной величины $\xi$ , число ${\mathsf E\,}|\xi|^k$ называется абсолютным -м моментом, ${\mathsf E\,}(\xi-{\mathsf E\,}\xi)^k$ называется центральным -м моментом, и ${\mathsf E\,}|\xi-{\mathsf E\,}\xi|^k$ - абсолютным центральным -м моментом} случайной величины $\xi$ . Число ${\mathsf D\,}\xi={\mathsf E\,}(\xi-{\mathsf E\,}\xi)^2$ (центральный момент второго порядка) называется дисперсией случайной величины $\xi$ .

Пример 52. Пусть, скажем, случайная величина $\xi$ принимает значение с вероятностью 0{,}99999 и значение 100 с вероятностью 0{,}00001 . Посмотрим, как моменты разных порядков реагируют на большие, но маловероятные значения случайной величины:

${\mathsf E\,}\,\xi\;&=&0\,\cdot \,0{,}99999\, + \,100\,\cdot\, 0{,}00001= \,0{,}001, \\ {\mathsf E\,}\xi^2&=&0^2\cdot 0{,}99999+ {100}^2\cdot 0{,}00001=0{,}1, \\ {\mathsf E\,}\xi^4&=&0^4\cdot 0{,}99999+{100}^4\cdot 0{,}00001=1\,000,\\ {\mathsf E\,}\xi^6&=&0^6\cdot 0{,}99999+{100}^6\cdot 0{,}00001=10\,000\,000.$

Пример 53. Дисперсия ${\mathsf D\,}\xi={\mathsf E\,}(\xi-{\mathsf E\,}\xi)^2$ есть "среднее значение квадрата отклонения случайной величины $\xi$ от своего среднего". Посмотрим, за что эта величина отвечает.

Пусть случайная величина $\xi$ принимает значения $\pm 1$ с равными вероятностями, а случайная величина $\eta$ - значения $\pm 10$ с равными вероятностями. Тогда ${\mathsf E\,}\xi={\mathsf E\,}\eta=0$ , поэтому ${\mathsf D\,}\xi={\mathsf E\,}\xi^2=1$ , ${\mathsf D\,}\eta={\mathsf E\,}\eta^2=100$ . Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг ее математического ожидания.

Определение 38. Число $\sigma=\sqrt{{\mathsf D\,}\xi}$ называют среднеквадратическим отклонением случайной величины $\xi$ .

Чтобы прояснить связь моментов разных порядков, докажем несколько неравенств. Во-первых, получим очевидное утверждение, обеспечивающее существование моментов меньших порядков, если существуют моменты более высокого порядка.

Теорема 31. Если существует момент порядка t>0 случайной величины $\xi$ , то существуют и ее моменты порядка при 0<s<t .

Доказательство. Для любого числа верно неравенство

$|x|^s\le \max\{\,|x|^t,\;1\}\,\le \,|x|^t+1.$

Действительно, $|x|^s\le |x|^t$ при |x|>1

, и $|x|^s\le 1$ при $|x|\le 1$ .

Из этого неравенства следует, что $|\xi(\omega)|^s\le |\xi(\omega)|^t+1$ для всех $\omega$ . Но следствие 11 позволяет из неравенства для случайных величин получить такое же неравенство для их математических ожиданий:

${\mathsf E\,}|\xi|^s\le{\mathsf E\,}|\xi|^t+1.$

Момент порядка

существует, т.е. ${\mathsf E\,}|\xi|^t<\infty$ . Поэтому и ${\mathsf E\,}|\xi|^s<\infty$ .

Докажем еще одно чрезвычайно полезное неравенство.

Теорема 32 (неравенство Йенсена). Пусть вещественнозначная функция "выпукла вниз", т.е. ее надграфик есть выпуклое множество. Тогда для любой случайной величины $\xi$ с конечным первым моментом верно неравенство: ${\mathsf E\,} g(\xi)\ge g({\mathsf E\,}\xi)$ . Для вогнутых функций знак неравенства меняется на противоположный.

Доказательство. Нам понадобится следующее свойство.

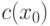Лемма 6. Пусть функция выпукла. Тогда для всякого x_0 найдется число c(x_0) такое, что при всех

$g(x)\ge g(x_0) + c(x_0)(x-x_0).$

Это свойство очевидно и означает, что график выпуклой функции лежит полностью выше любой из касательных к этому графику.

Возьмем в условиях леммы $x_0={\mathsf E\,}\xi$ , $x=\xi$ . Тогда

$g(\xi)\ge g({\mathsf E\,}\xi)+c({\mathsf E\,}\xi)(\xi-{\mathsf E\,}\xi).$

Вычислим математическое ожидание обеих частей неравенства. Так как ${\mathsf E\,}(\xi-{\mathsf E\,}\xi)=0$ , и неравенство между математическими ожиданиями сохраняется по следствию 11, то ${\mathsf E\,} g(\xi)\ge g({\mathsf E\,}\xi)$ .

Следующее неравенство связывает моменты разных порядков.

Следствие 13. Если ${\mathsf E\,}{|\xi|}^t<\infty$ , то для любого 0<s<t

$\sqrt[\mbox{\small $s$ }]{{\mathsf E\,}{|\xi|}^s} \le \sqrt[\mbox{\small $t$ }]{{\mathsf E\,}{|\xi|}^t}$

Доказательство. Поскольку 0<s<t , то $g(x)=|x|^{t/s}$ - выпуклая функция. По неравенству Йенсена для $\eta=|\xi|^s$ ,

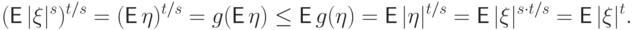
$({\mathsf E\,}{|\xi|^s})^{t/s}=({\mathsf E\,}\eta)^{t/s}=g({\mathsf E\,}\eta) \le {\mathsf E\,} g(\eta)= {\mathsf E\,}{|\eta|^{t/s}}={\mathsf E\,}{|\xi|^{s\cdot t/s}}= {\mathsf E\,}{|\xi|^t}.$

Осталось извлечь из обеих частей корень степени

.

Из неравенства Йенсена вытекают, например, неравенства:

$\begin{align*} \qquad\qquad{\mathsf E\,} e^{\xi} &\geq e^{{\mathsf E\,}\xi}, &{\mathsf E\,}\xi^2 &\geq ({\mathsf E\,}\xi)^2, &{\mathsf E\,}|\xi| &\geq |{\mathsf E\,}\xi|, \cr {\mathsf E\,} \ln\xi &\leq \ln({\mathsf E\,}\xi), &{\mathsf E\,} \frac{1}{\xi} &\geq \frac{1}{{\mathsf E\,}\xi}, &{\mathsf E\,} \sqrt{\mathstrut\xi} &\leq \sqrt{\mathstrut{\mathsf E\,}\xi}. \qquad\qquad \end{align*}$

Последние три неравенства верны для положительных $\xi$ .

Дальше >>

Введение в теорию вероятностей

Введение в теорию вероятностей

Числовые характеристики распределений

Дисперсия и моменты старших порядков

Вопросы и ответы

Студенты

Авторизоваться

Введение в теорию вероятностей

Введение в теорию вероятностей

Числовые характеристики распределений

Дисперсия и моменты старших порядков

Вопросы и ответы

Студенты