Условная вероятность и независимость
Формула полной вероятности
Пример 33.
Есть три завода, производящих одну и ту же продукцию. Первый завод производит 25%, второй завод - 35%, третий - 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти:
- вероятность купить бракованное изделие;
- условную вероятность того, что купленное изделие изготовлено первым заводом, если это изделие оказалось бракованным.
Первая вероятность равна доле бракованных изделий
в объеме всей продукции, т.е.  .
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
.
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
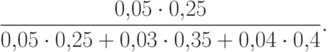
Определение 15.
Конечный или счетный набор попарно несовместных событий  таких,
что
таких,
что 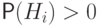 для всех
для всех  и
и 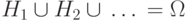 ,
называется полной группой событий или разбиением
пространства
,
называется полной группой событий или разбиением
пространства  .
.
События 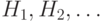 , образующие полную группу событий,
часто называют гипотезами. При подходящем
выборе гипотез для любого события
, образующие полную группу событий,
часто называют гипотезами. При подходящем
выборе гипотез для любого события  могут быть сравнительно просто
вычислены
могут быть сравнительно просто
вычислены  и
собственно
и
собственно  .
Как, используя эти данные, посчитать вероятность события
.
Как, используя эти данные, посчитать вероятность события  ?
?
Теорема 11 (формула полной вероятности).
Пусть дана полная группа событий  ,
,  , Тогда вероятность
любого события
, Тогда вероятность
любого события  может быть вычислена по формуле
может быть вычислена по формуле

Доказательство. Заметим, что

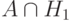 ,
,  , попарно
несовместны.
Поэтому
, попарно
несовместны.
Поэтому
 -аддитивность
вероятностной
меры, а в третьем - теорему 9
умножения вероятностей.
-аддитивность
вероятностной
меры, а в третьем - теорему 9
умножения вероятностей.Формула Байеса
Теорема 12 (формула Байеса).
Пусть 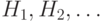 - полная группа событий, и
- полная группа событий, и  -
некоторое событие, вероятность которого положительна. Тогда условная
вероятность
того, что имело место событие
-
некоторое событие, вероятность которого положительна. Тогда условная
вероятность
того, что имело место событие 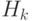 , если в результате эксперимента
наблюдалось событие
, если в результате эксперимента
наблюдалось событие  , может быть вычислена по формуле
, может быть вычислена по формуле
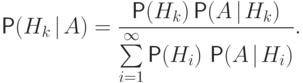
Доказательство. По определению условной вероятности,
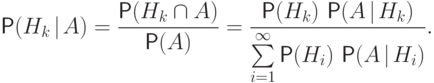
Пример 34.
Вернемся к примеру 33.
Изделие выбирается наудачу из всей произведенной продукции.
Рассмотрим три гипотезы:  ,
, 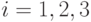 .
Вероятности этих событий даны:
.
Вероятности этих событий даны: 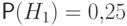 ,
, 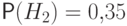 ,
, 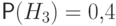 .
.
Пусть  .
Даны также условные вероятности
.
Даны также условные вероятности 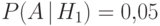 ,
, 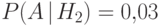 ,
, 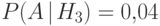 .
.
Убедитесь, что полученные нами в примере 33 вероятности совпадают с вероятностями, вычисленными по формуле полной вероятности и по формуле Байеса.
Вероятности  , вычисленные заранее, до проведения
эксперимента, называют априорными вероятностями ( a'priori - "до
опыта").
Условные вероятности
, вычисленные заранее, до проведения
эксперимента, называют априорными вероятностями ( a'priori - "до
опыта").
Условные вероятности 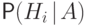 называют
апостериорными вероятностями ( a'posteriori - "после
опыта").
Формула Байеса позволяет переоценить заранее известные
вероятности после того, как получено знание о результате эксперимента.
Эта формула находит многочисленные применения в экономике, статистике,
социологии и т.п.
называют
апостериорными вероятностями ( a'posteriori - "после
опыта").
Формула Байеса позволяет переоценить заранее известные
вероятности после того, как получено знание о результате эксперимента.
Эта формула находит многочисленные применения в экономике, статистике,
социологии и т.п.
Пример 35.
Два стрелка подбрасывают монетку и выбирают, кто из них будет стрелять по
мишени (одной пулей).
Первый стрелок попадает по мишени с вероятностью  , второй
стрелок -
с вероятностью
, второй
стрелок -
с вероятностью  .
.
Можно сделать два предположения об эксперименте:  - стреляет 1-й стрелок (выпал герб) и
- стреляет 1-й стрелок (выпал герб) и  - стреляет 2-й стрелок
(выпала решка).
Априорные вероятности этих гипотез одинаковы:
- стреляет 2-й стрелок
(выпала решка).
Априорные вероятности этих гипотез одинаковы:  .
.
Как изменятся вероятности гипотез после проведения опыта?
Рассмотрим событие  - пуля попала в мишень. Известно, что
- пуля попала в мишень. Известно, что
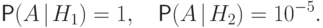
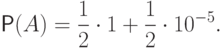
Предположим, что событие  произошло. Тогда по формуле Байеса
произошло. Тогда по формуле Байеса
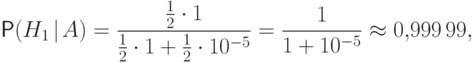
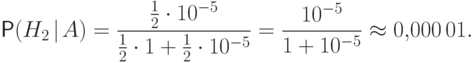
 раз
более вероятным,
чем выпадение решки.
раз
более вероятным,
чем выпадение решки.
