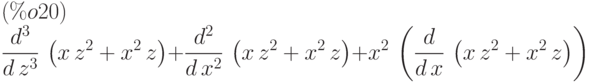Задачи высшей математики с Maxima

3.3.3 Непрерывные функции

Понятие непрерывности функции, так же как и понятие предела, является одним из основных понятий математического анализа.

3.3.3.1 Непрерывность функции в точке

Дадим два определения понятия непрерывности функции в точке.

Рис. 3.1. Определение непрерывной функции

Определение 1. Функция называется непрерывной в точке , если она удовлетворяет трем условиям: 1) определена в некоторой окрестности точки 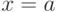, 2) существует конечный предел l этот предел равен значению функции в точке , т.е. 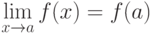. Очевидно, что непрерывность функции в данной точке выражается непрерывностью ее графика при прохождении данной точки.

Рассмотрим второе определение непрерывности функции в точке.

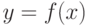Придадим аргументу приращение . Тогда функция получит приращение 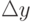, определяемое как разность наращенного и исходного значения функции: (см. рис. 3.1).

Определение 2. Функция 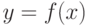называется непрерывной в точке , если она определена в некоторой окрестности точки 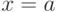, и приращение ее 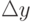в этой точке, соответствующее приращению 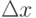, стремится к нулю при стремлении 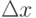к нулю: .

В руководствах по математическому анализу доказывается, что оба определения равносильны.

Пример исследования непрерывности функции с Maxima:

Функция

(%i16)	f(x):=1/(1+exp(1/(1-x)));

(%i17)	limit(f(x),x,1,plus);

(%i18)	limit(f(x),x,1,minus);

Пределы не совпадают, поэтому делаем вывод, что исследуемая функция разрывна.

3.3.3.2 Свойства непрерывных функций

1. Если функции и непрерывны в точке , то их сумма , произведение , и частное (при условии, что ) являются функциями, непрерывными в точке .
2. Если функция 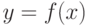непрерывна в точке и 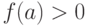, то существует такая окрестность точки a, в которой .
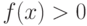3. Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке .

   Свойство 3 может быть записано в виде:

   
   т.е. под знаком непрерывной функции можно переходить к пределу.

Функция 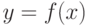называется непрерывной на промежутке , если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области их определения.

3.3.3.3 Точки разрыва функций и их классификация

Точка , принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва функции , если в этой точке нарушается условие непрерывности функции.

Если существуют конечные пределы 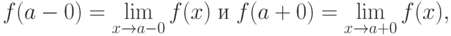причем не все три числа 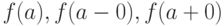равны между собой, то точка называется точкой разрыва 1 рода (существуют конечные односторонние пределы функции слева и справа, не равные друг другу).

Точки разрыва 1 рода подразделяются, в свою очередь, на точки устранимого разрыва (когда 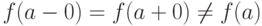, т.е. когда левый и правый пределы функции в точке a равны между собой, но не равны значению функции в этой точке) и на точки скачка (когда , т.е. когда левый и правый пределы функции в точке различны); в последнем случае разность называется скачком функции в точке .

Точки разрыва, не являющиеся точками разрыва 1 рода, называются точками разрыва 2 рода. В точках разрыва 2 рода не существует хотя бы один из односторонних пределов.

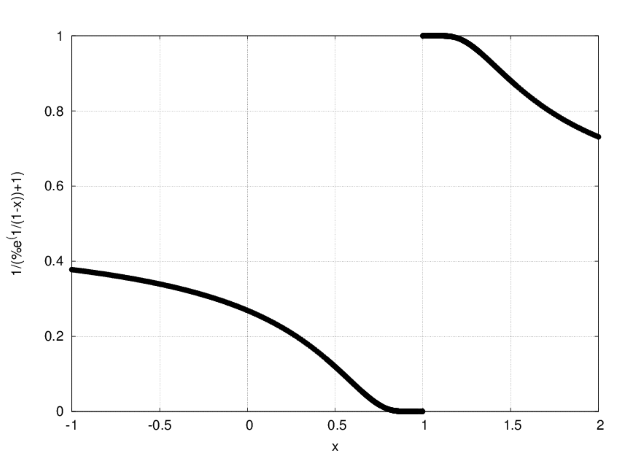
Рассмотрим предыдущий пример. Функция

увеличить изображение
Рис. 3.2. Разрыв исследуемой функции

Так как пределы 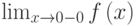и не совпадают, но оба конечны, делаем вывод о наличии точки разрыва первого рода при .

Графическую иллюстрацию получаем при помощи wxMaxima (см. рис. 3.2).

3.3.4 Дифференцирование с помощью пакета Maxima

Пакет Maxima предоставляет мощные средства для дифференцирования функций и вычисления дифференциалов. Для вычисления простейшей производной следует в командном окне после приглашения Maxima ввести команду следующего вида: diff(<функция>, <переменная>); где <функция> –– выражение, задающее функцию (не обязательно одной переменной), например x^2+2*x+1; <переменная> –– имя переменной, по которой будет вестись дифференцирование, например .

Примером вычисления производной может служить такая команда: diff(x^2+2*x+1,x);.

С помощью команды 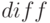можно вычислять производные высших порядков. При этом команда имеет следующий формат: 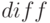(<функция>,<переменная>,<порядок>); где <порядок> — порядок вычисляемой производной.

В решениях некоторых примеров этой главы с помощью Maxima будут использованы дополнительные команды Maxima:

• (<выражение >), (<выражение >) — упрощение алгебраического выражения.
• (<выражение >), (<выражение >) — упрощение или подстановка тригонометрического выражения.
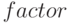• (<выражение>); –– разложить <выражение> на множители.
• (<выражение>,<old>=<new>); — подставить выражение <new> на место <old> в <выражении>.
• <переменная>:(<выр1>=<значение>,<выр2>); —- присвоить <переменной> значение выражения <выр2>, полученное разрешением уравнения <выр1>(<выр2>)=<значение>.
• — разложить функцию по формуле Тейлора с центром в точке 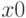до порядка n включительно.

3.3.4.1 Вычисление производных и дифференциалов

Для вычисления производной функции используется функция 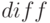, для вычисления производных различного порядка удобно создать пользовательскую функцию (в примере ниже — ):

(%i3)	f(x):=sin(9*x^2);

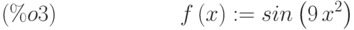
(%i4)	d1:diff(f(x),x,1);

(%i5)	d2:diff(f(x),x,2);

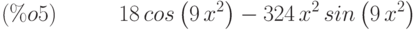
(%i6)	d3:diff(f(x),x,3);

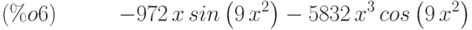
Пример вычисления дифференциала ( равноценно , не указана явно переменная дифференцирования):

(%i8)	diff(log(x));

Аналогичный подход применим и для функции нескольких переменных. Функция 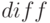с единственным аргументом — дифференцируемой функцией — возвращает полный дифференциал.

Пример:

(%i9)	diff(exp(x*y));

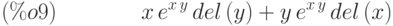
Пример:

(%i10)	diff(exp(x*y*z));

Если указать апостроф перед символом 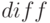, то производная не вычисляется и упрощение, обычно предусмотренное по умолчанию, не осуществляется.

Пример:

Создаём функцию :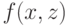

(%i18)	f(x,z):=x^2*z+z^2*x;

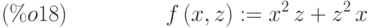
Вычисляем дифференциальное выражение:

(%i19)	diff (f(x,z), x, 2) + diff (f(x,z), z, 3) +
	diff (f(x,z), x) * x^2;

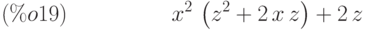
Производим формальное дифференцирование, не вычисляя непосредственно результат:

(%i20)	'diff (f(x,z), x, 2) + 'diff (f(x,z), z, 3) +
	'diff (f(x,z), x) * x^2;