| Россия |
Задачи высшей математики с Maxima
3.2 Задачи линейной алгебры
Пакет Maxima включает большое число функций для решения разнообразных задач линейной алгебры.
Рассмотрим основные функции, позволяющие оперировать матрицами и решать основные задачи линейной алгебры.
3.2.1 Простейшие операции с матрицами
В Maxima на матрицах определены обычные операции умножения на число, сложения и матричного умножения. Последнее реализуется с помощью бинарной операции "." (точка). Размерности матрицсомножителей должны быть согласованы.
Рассмотрим несколько примеров.
Создание двух прямоугольных матриц:
(%i1) a:matrix([1,2,3],[4,5,6]);
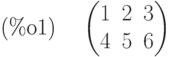
(%i2) b:matrix([2,2],[3,3],[4,4]);
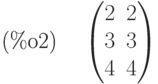
Функция 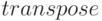 транспонирует матрицу:
транспонирует матрицу:
(%i1) a:matrix([1,2,3]); transpose(a);
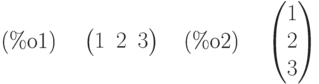
Умножение матрицы на число:
(%i2) c:b*2;
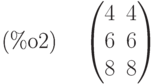
Сложение матриц (естественно, матрицы должны быть одинаковой формы, иначе возникает ошибка):
(%i4) b+c;
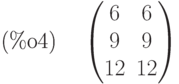
(%i5) a+b; fullmap: arguments must have same formal structure. – an error. To debug this try: debugmode(true);
Умножение матриц (в данном случаем исходные матрицы  и
и  согласованы по размерам):
согласованы по размерам):
(%i6) f:a.b;
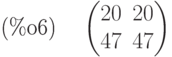
Если матрица — левый сомножитель, то правым сомножителем может быть не только вектор-столбец, но и вектор-строка и даже список.
Maxima позволяет также возводить матрицы в степень, но фактически эта операция применяется к каждому элементу.
3.2.2 Обращение матриц и вычисление определителей
Для обращения матриц используется функция  . Пример:
. Пример:
(%i1) a:matrix([1,2],[3,4]); b:invert(a); b.a;
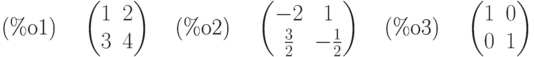
Определитель вычисляется функцией  :
:
(%i4) determinant(a);
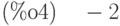
3.2.3 Характеристический полином, собственные числа и собственные векторы матрицы
Характеристический полином матрицы вычисляется функцией 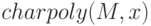 (
( — матрица,
— матрица,  — переменная, относительно которой строится полином).
— переменная, относительно которой строится полином).
Пример:
(%i6) charpoly(a,x);
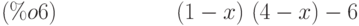
(%i7) ratsimp(%);

Корни характеристического полинома являются собственными числами матрицы.
Однако для вычисления собственных чисел и собственных векторов матрицы обычно используют специальные функции:  и
и  .
.
Функция  аналитически вычисляет собственные значения и собственные вектора матрицы, если это возможно. Она возвращает список, первый элемент которого — список собственных чисел (аналогично
аналитически вычисляет собственные значения и собственные вектора матрицы, если это возможно. Она возвращает список, первый элемент которого — список собственных чисел (аналогично  ), а далее идут собственные вектора, каждый из которых представлен как список своих проекций.
), а далее идут собственные вектора, каждый из которых представлен как список своих проекций.

(%i1) a:matrix([1,1,1],[2,2,2],[3,3,3]);
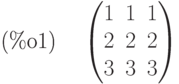
(%i2) eigenvalues(a);
![\parbox{8ex}{(\%o2)}[[0,6],[2,1]]](/sites/default/files/tex_cache/2182369562fe73de6dc2af76e2bec4a3.png)
(%i3) eigenvectors(a);
![\parbox{8ex}{(\%o3)}[[[0,6],[2,1]],[[[1,0,-1],[0,1,-1]],[[1,2,3]]]]](/sites/default/files/tex_cache/17114ed2d36281aa5abdf45787bc9e11.png)
Функция  отличается от функции
отличается от функции  тем, что возвращает нормированные на единицу собственные векторы.
тем, что возвращает нормированные на единицу собственные векторы.
3.2.4 Ортогонализация
Maxima включает специальную функцию для вычисления ортонормированного набора векторов из заданного. Используется стандартный алгоритм Грама-Шмидта.
Синтаксис вызова:  или
или 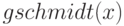 .
.
Аргумент функции — матрица или список. В качестве компонентов системы векторов, на базе которой строится ортонормированная система, рассматриваются строки матрицы  или подсписки списка
или подсписки списка  . Для использования данной функции необходимо явно загрузить пакет eigen.
. Для использования данной функции необходимо явно загрузить пакет eigen.
Пример:
(%i1) load("eigen");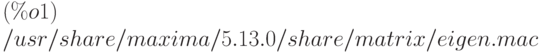
(%i2) x:matrix([1,2,3],[4,5,6]);

(%i3) y:gramschmidt(x);
![[[1,2,3],[\frac{{2}^{2}\,3}{7},\frac{3}{7},-\frac{2\,3}{7}]] \leqno{ (\%o3)
}](/sites/default/files/tex_cache/210ade7ef1b2e79a46a19e0a8717265b.png)
(%i4) ratsimp(%[1].%[2]);

3.2.5 Преобразование матрицы к треугольной форме
Преобразование матрицы к треугольной форме осуществляется методом исключения Гаусса посредством функции  (аналогичный результат даёт функция
(аналогичный результат даёт функция  ):
):
(%i1) a:matrix([1,2,3],[4,5,x],[6,7,y]);
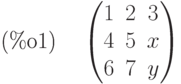
(%i2) b:echelon(a);
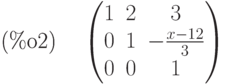
Отличия рассматриваемых функций в том, что  нормирует диагональный элемент на 1, а
нормирует диагональный элемент на 1, а  — нет. Обе функции используют алгоритм исключения Гаусса.
— нет. Обе функции используют алгоритм исключения Гаусса.
3.2.6 Вычисление ранга и миноров матрицы
Для расчёта ранга матрицы (порядка наибольшего невырожденного минора матрицы) используется функция  .
.
Пример:
(%i1) a:matrix([1,2,3,4],[2,5,6,9]);
Матрица  — невырожденная (две строки, ранг равен 2). Вычислим ранг вырожденной матрицы, содержащей линейно-зависимые строки.
— невырожденная (две строки, ранг равен 2). Вычислим ранг вырожденной матрицы, содержащей линейно-зависимые строки.
(%i1) a:matrix([1,2,3,4],[2,5,6,9]);
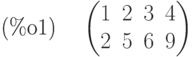
(%i2) rank(a);

(%i3) b:matrix([1,1],[2,2],[3,3],[4,5]);
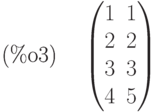
(%i4) rank(b);
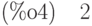
Минор матрицы вычисляется при помощи функции 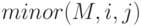 , где
, где  — матрица,
— матрица,  — индексы элемента, для которого вычисляется минор.
— индексы элемента, для которого вычисляется минор.
3.2.7 Решение матричных уравнений
Пусть дано матричное уравнение  , где
, где  — квадратная матрица размерности
— квадратная матрица размерности  ;
;  — матрица размерности
— матрица размерности  ;
;  — неизвестная матрица размерности
— неизвестная матрица размерности  . Пусть
. Пусть  — невырожденная матрица (т.е.
— невырожденная матрица (т.е. 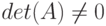 , тогда существует единственное решение этого уравнения. Решение можно найти по формуле
, тогда существует единственное решение этого уравнения. Решение можно найти по формуле 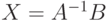
Пример: Найти решение матричного уравнения  , где
, где
![A = \left[ \begin{array}{ccc}
1 & 2 & 2\\
- 1 & - 1 & 3\\
2 & 5 & 0
\end{array} \right]$, \ $B = \left[ \begin{array}{c}
\begin{array}{cc}
\text{10} & 0
\end{array}\\
\begin{array}{cc}
- 2 & 5
\end{array}\\
\begin{array}{cc}
1 & 4
\end{array}
\end{array}
\right].](/sites/default/files/tex_cache/a2cc2f1423055e9b6ed64ab2191f3325.png)
Сначала зададим матрицы  и
и  :
:
(%i1) A: matrix( [1, 2, 2],[ -1, -1, 3], [2, 5, 0]);
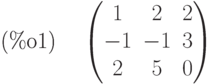
(%i2) B:matrix([10, 0],[-2, 5], [1, 4]);
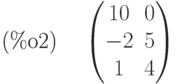
Проверим существование и единственность решения:
(%i3) determinant(A);
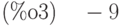
Матрица  невырожденная, значит, решение существует и единственно. Найдём его:
невырожденная, значит, решение существует и единственно. Найдём его:
(%i4) A1:invert(A); x:A1.B;
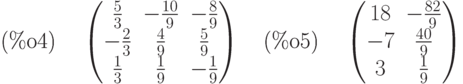
Выполним проверку:
(%i6) A.x-B;
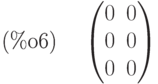
Аналогично решается матричное уравнение 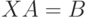 , где
, где  — квадратная матрица размерности
— квадратная матрица размерности 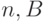 — матрица размерности
— матрица размерности  ,
,  — неизвестная матрица размерности
— неизвестная матрица размерности  . Если
. Если  — невырожденная матрица, то существует единственное решение
— невырожденная матрица, то существует единственное решение 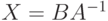 .
.
Пример: Найти решение  матичного уравнений
матичного уравнений  , где матрица
, где матрица  из предыдущей задачи,
из предыдущей задачи,  — заданная матрица. Аналогично предыдущему примеру, вычисляем решение:
— заданная матрица. Аналогично предыдущему примеру, вычисляем решение:
(%i10) C:matrix([10,0,-2],[5,1,4]); x:C.A1; x.A-C;
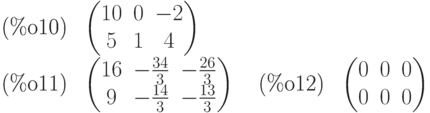
В общем случае (когда  — вырожденная матрица, или
— вырожденная матрица, или  — не квадратная матрица) матричное уравнение
— не квадратная матрица) матричное уравнение  можно решить при помощи функции
можно решить при помощи функции  .
.
Синтаксис вызова: ![solve([eq_1,eq_2 ... ,eq_n], [x_1,x_2,... ,x_m])](/sites/default/files/tex_cache/3a5b9e998218c13bdac8b2a9ccc234e9.png) , где
, где ![[eq_1,eq_2 ... ,eq_n]](/sites/default/files/tex_cache/c6a24b38b7a082d2355a7ac238181323.png) — список уравнений,
— список уравнений, ![[x_1,x_2,... ,x_m]](/sites/default/files/tex_cache/1c41d755a26442dc655c1a4d0c48907e.png) — список неизвестных, относительно которых осуществляется решение.
— список неизвестных, относительно которых осуществляется решение.
3.2.8 Специальные функции для решения систем линейных и полиномиальных уравнений
Функция ![linsolve([expr_1,expr_2,... ,expr_m], [x_1,x_2,... ,x_n])](/sites/default/files/tex_cache/bc5cd545c7e961c3720c536a2ef65b81.png) решает список одновременных линейных уравнений
решает список одновременных линейных уравнений ![[expr_1,expr_2,... ,expr_m]](/sites/default/files/tex_cache/22ead0c0d100ce7b352efda213236edf.png) относительно списка переменных
относительно списка переменных ![[x_1,... ,x_n]](/sites/default/files/tex_cache/85f9aad758680af9157c8bc08b627e91.png) .
.
Выражения ![[expr_1,... ,expr_n]](/sites/default/files/tex_cache/ec2d639d563710ca2229e4b8608eb2cb.png) могут быть полиномами указанных переменных и представляться в виде уравнений.
могут быть полиномами указанных переменных и представляться в виде уравнений.
Пример: Решить системы линейных уравнений
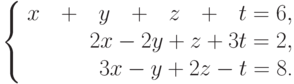
Решение в Maxima:
(%i1) ex1:x+y+z+t=6; ex2:2*x-2*y+z+3*t=2; ex3:3*x-y+2*z-t=8; linsolve([ex1,ex2,ex3],[x,y,z,t]);
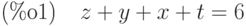
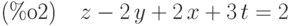
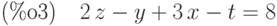
![\parbox{8ex}{(\%o4)}[x=-\frac{3\,\%r1-14}{4},y=-\frac{\%r1-10}{4},z=\%r1,t=0]](/sites/default/files/tex_cache/2346852af0023b23ec768c8881be645f.png)
Таким образом общее решение имеет вид:  , где
, где  — произвольная постоянная. Ей можно задавать произвольные действительные значения. При каждом значении c получается частное решение. Например, при
— произвольная постоянная. Ей можно задавать произвольные действительные значения. При каждом значении c получается частное решение. Например, при 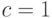 получается частное решение
получается частное решение
(%i5) ev(%),%r1=1;
![[x=\frac{11}{4},y=\frac{9}{4},z=1,t=0]\leqno{ (\%o5) }](/sites/default/files/tex_cache/aac09dfbf1dc9154461c020978f25d59.png)
Способ представления решения зависит от флага  (по умолчанию
(по умолчанию 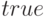 ). Если указанный флаг установлен в
). Если указанный флаг установлен в 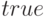 , решение недоопределённых систем включает параметры
, решение недоопределённых систем включает параметры  и т.д. Если флаг
и т.д. Если флаг  установлен в
установлен в 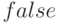 , связанные переменные выражаются через свободные.
, связанные переменные выражаются через свободные.
Во многом аналогичный результат позволяет получить функция  (фактически, это надстройка над
(фактически, это надстройка над  ).
).
Функция ![algsys([expr_1,expr_2,... ,expr_m], [x_1,x_2,... ,x_n])](/sites/default/files/tex_cache/e32727d1a83fc8b45603c51233b79bf5.png) решает систему
решает систему ![[expr_1 = 0,expr_2 = 0,... ,expr_m = 0]](/sites/default/files/tex_cache/16067487da6ec1d989a4889a1cc1df84.png) полиномиальных уравнений относительно списка переменных
полиномиальных уравнений относительно списка переменных ![[x_1,... ,x_n]](/sites/default/files/tex_cache/85f9aad758680af9157c8bc08b627e91.png) .
.
Выражения ![[expr_1,... ,expr_n]](/sites/default/files/tex_cache/ec2d639d563710ca2229e4b8608eb2cb.png) могут быть представлены и в виде уравнений. Количество уравнений может превышать количество неизвестных и наоборот.
могут быть представлены и в виде уравнений. Количество уравнений может превышать количество неизвестных и наоборот.
Пример:
(%i6) e1: 2*x*(1 - a1) - 2*(x - 1)*a2; e2: a2 - a1; e3: a1*(-y - x^2 + 1); e4: a2*(y - (x - 1)^2);


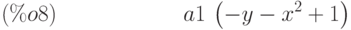

(%i10) algsys ([e1, e2, e3, e4], [x, y, a1, a2]);
![[[x=0,y=\%r2,a1=0,a2=0],[x=1,y=0,a1=1,a2=1]]\leqno{ (\%o10) }](/sites/default/files/tex_cache/a35dfea8f8d1e3290e0dcc5a78e0fd3c.png)
Для вычисления корней единичных полиномиальных уравнений используется функция  .
.
Варианты синтаксиса:
-
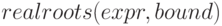 ;
; -
 ;
; -
 ;
; -
 .
.
Функция находит все корни выражения 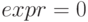 или уравнения
или уравнения 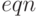 . Функция строит последовательность Штурма для изоляции каждого корня и использует алгоритм деления пополам для уточнения корня с точностью
. Функция строит последовательность Штурма для изоляции каждого корня и использует алгоритм деления пополам для уточнения корня с точностью 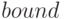 или с точностью, заданной по умолчанию.
или с точностью, заданной по умолчанию.
Пример:
(%i11) realroots (2 - x + x^5, 5e-6);
![[x=-\frac{664361}{524288}]\leqno{ (\%o11) }](/sites/default/files/tex_cache/87cac747359ea78dcd1e3814de7dc6f2.png)
(%i12) float(%);
![[x=-1.267168045043945]\leqno{ (\%o12) }](/sites/default/files/tex_cache/3f14ad5dd266aff3ef59f69c40893ad0.png)
(%i13) ev(2-x+x^5,%[1]);

Все корни полинома (действительные и комплексные) можно найти при помощи функции 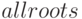 . Способ представления решения определяется переменной
. Способ представления решения определяется переменной  (по умолчанию
(по умолчанию 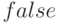 ; если установить в
; если установить в 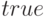 , то функция возвращает результат факторизации). Алгоритм поиска корней получисленный.
, то функция возвращает результат факторизации). Алгоритм поиска корней получисленный.
Пример:
(%i1) eqn:x^4+1; soln:allroots (eqn);
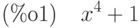
![\parbox{8ex}{(\%o2) }
[x=0.70710678118655\%i+0.70710678118655,\\
x=0.70710678118655-0.70710678118655\%i,\\
x=0.70710678118655\%i-0.70710678118655,\\
x=-0.70710678118655\%i-0.70710678118655]](/sites/default/files/tex_cache/3103b1993b07ff6c6d28c10365c2749b.png)
Количество действительных корней уравнения в некотором интервале возвращает функция  (синтаксис
(синтаксис 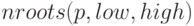 ).
).
Пример: (находим число корней уравнения на отрезке [-6, 9]):
(%i1) p: x^10 - 2*x^4 + 1/2$ nroots (p, -6, 9);

Для преобразования уравнений используются функции  и
и 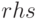 , позволяющие выделить левую и правую часть уравнения соответственно.
, позволяющие выделить левую и правую часть уравнения соответственно.
Пример:
(%i1) eqn:x^2+x+1=(x-1)^3;
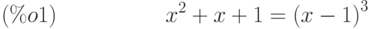
(%i2) lhs(eqn);

(%i3) rhs(eqn);

Упрощение систем уравнений достигается функцией  , позволяющей исключить те или иные переменные.
, позволяющей исключить те или иные переменные.
Вызов ![eliminate([eqn_1,...,eqn_n], [x_1,... ,x_k])](/sites/default/files/tex_cache/641cff9c7a40c82a5feb25b07dee487c.png) исключает переменные
исключает переменные ![[x_1,... ,x_k]](/sites/default/files/tex_cache/ed77a67039027257dd494d3176350c8d.png) из указанных выражений.
из указанных выражений.
Пример:
(%i1) expr1: 2*x^2 + y*x + z; expr2: 3*x + 5*y - z - 1; expr3: z^2 + x - y^2 + 5;



(%i4) eliminate ([expr3, expr2, expr1], [y, z]);
![(\%o4)\ [7425{x}^{8}-1170{x}^{7}+1299{x}^{6}+12076{x}^{5}+22887{x}^{4}-
5154{x}^{3}-1291{x}^{2}+7688x+15376]](/sites/default/files/tex_cache/5199fa711be49343b670f27b93da1beb.png)

