НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 3: Задачи высшей математики с Maxima

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

3.8.5 Дополнительные возможности решения ОДУ

3.8.5.1 Пакет contrib_ode

Как видно из описания возможностей Maxima выше, возможности основной функции для аналитического решения ОДУ — функции ode2 — весьма ограничены. Для расширения возможностей решения ОДУ первого и второго порядка в последних версиях Maxima существует пакет расширения contrib_ode. При помощи возможно решение уравнений Клеро, Лагранжа, Риккати и др. В общем случае результат — список решений. Для некоторых уравнений (в частности Риккати) решение представляется в форме другого ОДУ — результата замены переменных. Функция contrib_ode реализует методы факторизации ( factorization ), Клеро (Clairault), Лагранжа (Lagrange), Риккати (Riccati), Абеля (Abel) и метод симметрии Ли (Lie symmetry method).

Для использования пакет contrib_ode необходимо загрузить:

(%i1)	load("contrib_ode")$

Пример решения ОДУ с использованием функции contrib_ode :

(%i2)	eqn:x*'diff(y,x)^2-(1+x*y)*'diff(y,x)+y=0;

$x\,{\left( \frac{d}{d\,x}\,y\right) }^{2}-\left( x\,y+1\right) \,\left( \frac{d}{d\,x}\,y\right) +y=0\leqno{(\%o2) }$

(%i3)	contrib_ode(eqn,y,x);

$x\,{\left( \frac{d}{d\,x}\,y\right) }^{2}-\left( x\,y+1\right) \,\left( \frac{d}{d\,x}\,y\right) +y=0\leqno{(\%t3) }$

first order equation not linear in y'

$[y=log\left( x\right) +\%c,y=\%c\,{e}^{x}]\leqno{(\%o3) }$

(%i4)	method;

$factor\leqno{(\%o4) }$

Достоинство contrib_ode — возможность решения нелинейных ОДУ первого порядка, т.к. они могут иметь в общем случае несколько решений, результат представляется в виде списка.

Синтаксис вызова contrib_ode не отличается от синтаксиса вызова ode2 .

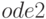Рассмотрим примеры решения других типов уравнений.

3.8.5.2 Уравнения Клеро и Лагранжа

Уравнение Клеро

(%i1)	load("contrib_ode")$
(%i2)	eqn:'diff(y,x)^2+x*'diff(y,x)-y=0;

${\left( \frac{d}{d\,x}\,y\right) }^{2}+x\,\left( \frac{d}{d\,x}\,y\right) -y=0\leqno{(\%o2) }$

(%i3)	contrib_ode(eqn,y,x);

${\left( \frac{d}{d\,x}\,y\right) }^{2}+x\,\left( \frac{d}{d\,x}\,y\right) -y=0\leqno{(\%t3) }$

first order equation not linear in y'

$[y=\%c\,x+{\%c}^{2},y=-\frac{{x}^{2}}{4}]\leqno{(\%o3) }$

(%i4)	method;

$clairault\leqno{(\%o4) }$

Уравнение Лагранжа

(%i5)	leq:y=(1+'diff(y,x))*x+('diff(y,x))^2;

$y={\left( \frac{d}{d\,x}\,y\right) }^{2}+x\,\left( \frac{d}{d\,x}\,y+1\right) \leqno{(\%o5) }$

(%i6)	contrib_ode(leq,y,x);

$y={\left( \frac{d}{d\,x}\,y\right) }^{2}+x\,\left( \frac{d}{d\,x}\,y+1\right)\leqno{(\%t6)}$

first order equation not linear in y'

$[[x={e}^{-\%t}\,\left( \%c-2\,\left( \%t-1\right) \,{e}^{\%t}\right) ,y=\left( \%t+1\right) \,x+{\%t}^{2}]]\leqno{(\%o6) }$

(%i7)	method;

$lagrange\leqno{(\%o7) }$

В некоторых случаях возможно только решение в параметрической форме. Пример ( $\%t$ — параметр):

(%i8	 eqn:'diff(y,x)=(x+y)^2;

$\frac{d}{d\,x}\,y={\left( y+x\right) }^{2}\leqno{(\%o8) }$

(%i9)	contrib_ode(eqn,y,x);

$[[x=\%c-atan\left( \sqrt{\%t}\right) ,y=-x-\sqrt{\%t}],\leqno{(\%o9) }$

$[x=atan\left( \sqrt{\%t}\right) +\%c,y=\sqrt{\%t}-x]]$

(%i10)	method;

$lagrange\leqno{(\%o10) }$

3.8.5.3 Другие задачи с использованием contrib_ode

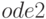Пакет contrib_ode позволяет решать дифференциальные уравнения, не разрешимые при помощи ode2 непосредственно. Пример — обобщённые однородные уравнения (см. выше). Представленные задачи используют методы Абеля и симметрии Ли.

(%i11)	eqn:(2*x-y+4)*'diff(y,x)+(x-2*y+5)=0;

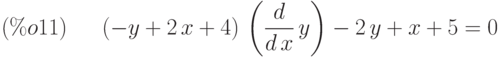
$\left( -y+2\,x+4\right) \,\left( \frac{d}{d\,x}\,y\right) -2\,y+x+5=0\leqno{(\%o11) }$

(%i12)	contrib_ode(eqn,y,x);

$\parbox{8ex}{(\%o12)}[\frac{log\left(3-\frac{2(2x+4)-x-5}{-y+2x+4}\right)-3log\left(1-\frac{2(2x+4)-x-5}{-y+2x+4}\right)+2log\left(-\frac{2(2x+4)-x-5}{4(-y+2x+4)}\right)}{2} =$\\ $log(x + 1)+\%c]$

(%i13)	method;

$abel2\leqno{(\%o13) }$

(%i14)	eqn1:'diff(y,x)=(1-3*x-3*y)/(1+x+y);

$\frac{d}{d\,x}\,y=\frac{-3\,y-3\,x+1}{y+x+1}\leqno{(\%o14) }$

(%i15)	contrib_ode(eqn1,y,x);

$[\frac{2\,log\left( y+x-1\right) +y+3\,x}{2}=\%c]\leqno{(\%o15) }$

(%i16)	method;

$lie\leqno{(\%o16) }$

3.8.5.4 Решение однородных линейных уравнений

Другие полезные функции пакета contrib_ode: odelin и ode_check .

Функция odelin решает однородные линейные уравнения первого и второго порядка, и возвращает фундаментальное решение ОДУ.

Пример:

(%i4)	odelin(x*(x+1)*'diff(y,x,2)+(x+5)*'diff(y,x,1)+(-4)*y,y,x);

...trying factor method...
solving 7 equations in 4 variables...
trying the Bessel solver...solving 1 equations in 2 variables...
trying the F01 solver...
solving 1 equations in 3 variables...
trying the spherodial wave solver...
solving 1 equations in 4 variables...
trying the square root Bessel solver...
solving 1 equations in 2 variables...
trying the 2F1 solver...
solving 9 equations in 5 variables

${\frac{gauss\_a\left( -6,-2,-3,-x\right) }{{x}^{4}},\frac{gauss\_b\left( -6,-2,-3,-x\right) }{{x}^{4}}}\leqno{(\%o4) }$

Примечание: функции gauss_a и gauss_b — специальные функции, представляющие собой решения гипергеометрического уравнения.

Функция ode_check позволяет подставить в ОДУ найденное решение.

Пример:

(%i1)	load("contrib_ode")$
(%i2)	eqn:(1+x^2)*'diff(y,x,2)-2*x*'diff(y,x);

$\left( {x}^{2}+1\right) \,\left( \frac{{d}^{2}}{d\,{x}^{2}}\,y\right) -2\,x\,\left( \frac{d}{d\,x}\,y\right) \leqno{(\%o2) }$

(%i3)	odelin(eqn,y,x);
...trying factor method...solving 7 equations in 4 variables

${1,x\,\left( {x}^{2}+3\right) }\leqno{(\%o3) }$

(%i4)	ode_check(eqn,y=x*(x^2+3));

$0\leqno{(\%o4) }$

(%i5)	ode_check(eqn,y=1);

$0\leqno{(\%o5) }$

Дальше >>

Компьютерная математика с Maxima

Компьютерная математика с Maxima

Задачи высшей математики с Maxima

3.8.5 Дополнительные возможности решения ОДУ

3.8.5.1 Пакет contrib_ode

3.8.5.2 Уравнения Клеро и Лагранжа

3.8.5.3 Другие задачи с использованием contrib_ode

3.8.5.4 Решение однородных линейных уравнений

Вопросы и ответы

Студенты

Авторизоваться

Компьютерная математика с Maxima

Компьютерная математика с Maxima

Задачи высшей математики с Maxima

3.8.5 Дополнительные возможности решения ОДУ

3.8.5.1 Пакет contrib_ode

3.8.5.2 Уравнения Клеро и Лагранжа

3.8.5.3 Другие задачи с использованием contrib_ode

3.8.5.4 Решение однородных линейных уравнений

Вопросы и ответы

Студенты