Компьютерная математика с Maxima

:

Компьютерная математика с Maxima
[+]
Опубликован: 24.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux
Лекция 3:

Задачи высшей математики с Maxima
A
|
версия для печати
< Лекция 2 || Лекция 3: 123456789101112131415 || Лекция 4 >

3.9.5 Ряд Фурье для функций с периодом 2l

Пусть f(x) — периодичная с периодом 2\ell\ \left(\ell \ne \pi \right) функция, которая на отрезке [-\ell ,\ell] удовлетворяет условиям теоремы Дирихле. Разложим её на этом отрезке в ряд Фурье. Обозначим

x=\frac{\ell t}{\pi } . ( 3.3)

Тогда

\[f(x)=f\left(\frac{\ell t}{\pi } \right)=\varphi (t)\]

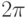Функция \varphi (t) — уже 2\pi–периодическая функция, так как

\[\varphi (t+2\pi )=f\left(\frac{\ell }{\pi } (t+2\pi )\right)=f\left(\frac{\ell t}{\pi } +2\ell \right)=f\left(\frac{\ell t}{\pi } \right)=\varphi (t).\]

Функцию \varphi (t) разложим в ряд Фурье на отрезке [-\pi ,\pi]

\varphi (t)=f\left(\frac{\ell t}{\pi } \right)=\frac{a_{0} }{2} +\sum _{n=1}^{\infty }\left(a_{n} \cos (nt)+b_{n} \sin (nt)\right) \dots ( 3.4)

Коэффициенты этого ряда вычисляются по формулам:

a_{n} =\frac{1}{\pi } \int _{-\pi }^{\pi }f\left(\frac{\ell t}{\pi } \right) \cos (nt)dt,n=0,1,\dots , ( 3.5)
b_{n} =\frac{1}{\pi } \int _{-\pi }^{\pi }f\left(\frac{\ell t}{\pi } \right) \sin (nt)dt,n=1,2,\dots ( 3.6)

Возвращаясь к прежней переменной x, из равенства (3.3) имеем t=\frac{\pi x}{\ell }. Тогда ряд (3.4) можно представить в виде

f(x)=\frac{a_{0} }{2} +\sum _{n=1}^{\infty }\left(a_{n} \cos (\frac{n\pi x}{\ell } )+b_{n} \sin (\frac{n\pi x}{\ell } )\right). ( 3.7)

В интегралах (3.5) и (3.6) произведём замену переменной:

a_{n} =\frac{1}{\pi } \int _{-\pi }^{\pi }f\left(\frac{\ell t}{\pi } \right)\cos (nt)dt= \frac{1}{\ell } \int _{-\ell }^{\ell }f(x)\cos (\frac{n\pi x}{\ell } )dx,n=0,1,\dots\\ b_{n} =\cfrac{1}{\pi } \displaystyle\int _{-\pi }^{\pi }f\left(\frac{\ell t}{\pi } \right)\sin (t)dt=\cfrac{1}{\ell } \displaystyle\int _{-\ell }^{\ell }f(x)\sin (\frac{n\pi x}{\ell } )dx, n=1,2,\dots.

Если f(x) — чётная на \left[-\ell ,\ell \right] функция, то b_n = 0 (n = 1, 2,...), а a_{n} = \cfrac{2}{\ell } \displaystyle\int _{0}^{\ell }f(x)\cos (\frac{n\pi x}{\ell } )dx,\ (n=0,1,\dots),, ряд Фурье такой функции имеет вид:

\[f(x)=\frac{a_{0} }{2} +\sum _{n=1}^{\infty }a_{n} \cos (\frac{n\pi x}{\ell } ) .\]

Если f(x) — нечётная на [-\ell ,\ell ] функция, то a_n = 0 (n = 0, 1, 2,...),

b_{n} =\cfrac{2}{\ell } \displaystyle\int _{0}^{\ell }f(x)\sin (\frac{n\pi x}{\ell } ) dx,\ (n=1,2,\dots )
, ряд Фурье имеет вид:

\[f(x)=\sum _{n=1}^{\infty } b_{n} \sin (\frac{n\pi x}{\ell } )dx.\]

Пример: Разложить в ряд Фурье периодическую с периодом T =2 функцию f(x), заданную формулой

f(x) = \begin{cases} x, &\mbox{если } \, 0<x\le 1 \\ 0, &\mbox{если } \, -1<x\le 0 \end{cases}.

Эта функция на отрезке [-1, 1] удовлетворяет условиям теоремы Дирихле. Ряд Фурье для данной функции:

\[f(x)=\frac{1}{4} -\frac{2}{\pi ^{2} } \sum _{k=0}^{\infty }\frac{\cos ((2k+1)x)}{(2k+1)^{2} } +\frac{1}{\pi } \sum _{k=1}^{\infty }\frac{(-1)^{k+1} }{k} \sin (k\pi x)\]

Сумма этого ряда в точках x=\pm 1,\pm 3,\dots равна \cfrac{1}{2}.

Рассмотрим видоизменение функции Maxima, необходимой для вычисления коэффициентов ряда Фурье для функции с периодом [-\ell, \ell]. Рассмотрим текст функции fun12l:

fun12l(x,n,l,f1,f2):=(for k:0 thru n do
	a[k]:1/l*(integrate(f1*cos(%pi*k*x/l),x,-l,0)
	+integrate(f2*cos(%pi*k*x/l),x,0,l)),
for k:1 thru n do b[k]:1/l*(integrate(f1*sin(%pi*k*x/l),x,-l,0)+
	integrate(f2*sin(%pi*k*x/l),x,0,l)),
	a[0]/2+sum(a[k]*cos(%pi*k*x/l),k,1,n)+
	sum(b[k]*sin(%pi*k*x/l),k,1,n))$

Основное изменение по сравнение с вариантами, приведёнными выше — использование тригонометрических функций \sin \left( \frac{\pi k x}{\ell} \right) и \sin \left( \frac{\pi k x}{\ell} \right)

Вывод Maxima для первых семи членов ряда Фурье:

(%i6)	fun12l(x,7,1,0,x);
(\%o6)\ \frac{sin\left( 7\,\pi \,x\right) }{7\,\pi }-\frac{2\,cos\left( 7\,\pi \,x\right) }{49\,{\pi }^{2}}-\frac{sin\left( 6\,\pi \,x\right) }{6\,\pi }+\frac{sin\left( 5\,\pi \,x\right) }{5\,\pi }-\frac{2\,cos\left( 5\,\pi \,x\right) }{25\,{\pi }^{2}}-\frac{sin\left( 4\,\pi \,x\right) }{4\,\pi }+\frac{sin\left( 3\,\pi \,x\right) }{3\,\pi }-\frac{2\,cos\left( 3\,\pi \,x\right) }{9\,{\pi }^{2}}-\frac{sin\left( 2\,\pi \,x\right) }{2\,\pi }+\frac{sin\left( \pi \,x\right) }{\pi }-\frac{2\,cos\left( \pi \,x\right) }{{\pi }^{2}}+\frac{1}{4}

Для построения графика собственно анализируемой функции (её представляет кусочно-непрерывная функция f(x)) и частичной суммы её ряда Фурье из результатов разложения формируем новую функцию g(x), после чего стандартной командой строим график:

(%i7)	g(x):="%$
(%i8)	f(x):=(if x<0 then 0 else x)$
(%i9)	wxplot2d([g(x),f(x)], [x,-2.2,1.6]);

Графическая иллюстрация, показывающая сопоставление рассматриваемой функции и ряда Фурье на заданном отрезке — на рис. 3.22.

График функции f(x) и суммы первых семи членов ряда Фурье

увеличить изображение
Рис. 3.22. График функции f(x) и суммы первых семи членов ряда Фурье

3.9.6 Комплексная форма ряда Фурье

Пусть функция f(x) на \left[-\pi ,\pi \right] разложена в ряд Фурье

f(x)=\frac{a_{0} }{2} +\sum _{n=1}^{\infty }\left(a_{n} \cos (x)+b_{n} \sin (x)\right) . ( 3.8)

Воспользуемся формулами Эйлера:

\[\cos (nx)=\frac{e^{inx} +e^{-inx} }{2} ,\ \sin (nx)=\frac{e^{inx} -e^{-inx} }{2i} .\]

Подставим эти выражения в ряд (3.8), имеем:

f(x)&=\frac{a_{0} }{2} +\sum _{n=1}^{\infty} \left(a_{n} \frac{e^{inx} +e^{-inx} }{2} + b_{n} \frac{e^{inx} -e^{-inx} }{2i} \right) = \\ &=\frac{a_{0} }{2} + \sum _{n=1}^{\infty }\left( a_{n} \frac{e^{inx}+e^{-inx} }{2} - ib_{n} \frac{e^{inx} -e^{-inx} }{2} \right) = \\ &=\frac{a_{0} }{2}+\sum _{n=1}^{\infty }\left( \frac{a_{n} -ib_{n} }{2} \cdot e^{inx} +\frac{a_{n} +ib_{n} }{2} \cdot e^{-inx} \right).

Обозначим:

\frac{a_{0} }{2} =c_{0} ,\ \frac{a_{n} -ib_{n} }{2} =c_{n} ,\ \frac{a_{n} +ib_{n} }{2} =c_{-n} . ( 3.9)

Тогда

f(x) &=c_{0} +\sum _{n=1}^{\infty }\left(c_{n} \cdot e^{inx} +c_{-n} e^{-inx} \right) = \\ &= c_{0} +\sum _{n=1}^{\infty }c_{n} e^{inx} +\sum _{n=1}^{\infty }c_{-n} e^{-inx} = \\ &= c_{0} +\sum _{n=1}^{\infty }c_{n} e^{inx} +\sum _{n=-\infty }^{n=-1}c_{n} e^{inx} =\sum _{n=-\infty }^{\infty }c_{n} e^{inx} .

Следовательно

f(x)=\sum _{n=-\infty }^{\infty }c_{n} e^{inx} ( 3.10)

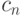Выражение (3.10) называется комплексной формой ряда Фурье функции f(x) с комплексными коэффициентами Фурье c_n. Коэффициенты Фурье 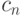c_n вычисляются по формулам (n=0, \pm 1, \pm 2,\dots):

c_{n} &=\frac{1}{2} \left(a_{n} -ib_{n} \right)= \frac{1}{2\pi} \int _{-\pi }^{\pi }f(x)\left[\cos (nx)-i\sin (nx)\right]dx=\\ &=\frac{1}{2\pi } \int _{-\pi }^{\pi }f(x)\left[\cos (-nx)+i\sin (-nx)\right]dx=\frac{1}{2\pi } \int _{-\pi }^{\pi }f(x)e^{-inx} dx.

Если f(x) — периодическая с периодом 2\ell функция, то её комплексный ряд Фурье имеет вид:

\[f(x)=\sum _{n=-\infty }^{\infty }c_{n} e^{\cfrac{in\pi x}{\ell } } ,\]
а коэффициенты Фурье определяются по формуле

\[c_{n} =\frac{1}{2\ell } \int _{-\ell }^{\ell }f(x )e^{\cfrac{-in\pi x}{\ell }}dx.\]

Пример: Разложить в ряд Фурье с комплексными коэффициентами периодическую с периодом l = 2 функцию, заданную на отрезке [-1, 1] равенством f(x) = x^2.

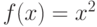(%i1)	n:5$ f:x^2$ l:1$ c(k):=
	1/2/l*integrate(f*exp(-%i*%pi*k*x/l),x,-l,l)$
	z:makelist(k-6, k, 1, 2*n+1)$
	cr:makelist(c(z[k]),k,1,2*n+1)$
	fk:makelist(cr[k]*exp(%i*%pi*z[k]*x/l),k,1,2*n+1)$
	g:sum(fk[k],k,1,2*n+1)$
	gend:trigreduce(ratsimp(rectform(g)));
(\%o9) \\ \frac{-144\,\mathrm{cos}\left( 5\,\pi \,x\right) +225\,\mathrm{cos}\left( 4\,\pi \,x\right) -400\,\mathrm{cos}\left( 3\,\pi \,x\right) +900\,\mathrm{cos}\left( 2\,\pi \,x\right) -3600\,\mathrm{cos}\left( \pi \,x\right) +300\,{\pi }^{2}}{900\,{\pi }^{2}}

В данном примере члены частичной суммы ряда Фурье представляются списком. В представленном вычислении z = -5, -4,... , 4, 5. Список cr содержит коэффициенты ряда в комплексной форме (при суммировании от -n до n индекс элемента ряда содержится в z[k]). Собственно члены ряда Фурье скомпонованы в список fk, после суммирования которого получаем сумму ряда (выражение g). Для построения графика g(x) необходимо упростить выражение g (см. пример, результат упрощения — выражение gend). Очевидно, что для просмотра промежуточных результатов (они довольно объёмные) терминальные символы $ можно заменить на ;.

3.9.7 Дополнительные возможности: пакет fourie

Пакет расширения fourie предназначен для расчёта коэффициентов тригонометрических рядов Фурье, а также интеграла Фурье. Функции, входящие в состав пакета, позволяют находить точное аналитическое выражение всех, а не первых нескольких коэффициентов ряда Фурье.

Функция fourier позволяет вычислить коэффициенты ряда Фурье (синтаксис вызова: fourier(f,x,p)), которая возвращает список коэффициентов Фурье f(x), определённых на интервале [-p,p]. Собственно ряд Фурье позволяет построить функция fourexpand (синтаксис вызова fourexpand(l,x,p,limit)), которая конструирует и возвращает ряд Фурье, используя список коэффициентов Фурье l (limit может быть и бесконечным, равным inf).

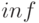Коэффициенты рядов Фурье по синусам и по косинусам вычисляются функциями fourcos(f,x,p) foursin(f,x,p) (синтаксис и аналогичны функции fourier).

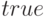Вычисления и подстановка \cos n\pi и \sin n\pi осуществляется специальной функцией foursimp(l). Управление подстановкой осуществляется посредством флагов sinnpiflag и cosnpiflag (если они установлены в true, вычисление и подстановка выполняются, это режим по умолчанию).

Для управления процессом разложения различных функций в ряд Фурье предусмотрены следующие функции:

  1. remfun. Синтаксис вызова remfun(f,expr) или remfun(f,expr,x). Данная функция позволяет заменить все вхождения функции f(arg) в выражении expr на arg (в форме remfun(f,expr,x) замена осуществляется, только если arg содержит x);
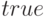  2. funp. Данная функция (синтаксис вызова funp(f,expr) или funp(f,expr,x)) возвращает true, если выражение expr содержит функцию f или конкретно f(x);
  3. absint. Данная функция позволяет вычислить неопределённый или определённый интеграл абсолютных значений функции f (её определение может включать выражения abs(x), abs(sin(x)), abs(a) * exp(-abs(b) * abs(x)). Синтаксис вызова absint(f,x,halfplane) (halfplane = (pos,neg,both) — часть числовой оси), absint(f,x) (неопределённый интеграл по положительной полуоси), absint(f,x,a,b) (определённый интеграл).

Общую форму ряда Фурье (после подстановки и упрощения) позволяет построить функция totalfourier(f,x,p).

Коэффициенты интеграла Фурье на интервале (- inf, inf) позволяет вычислить функция fourint(f,x), интеграла по косинусам или синусам на интервале (0, inf) — функции fourintcos(f,x) и fourintsin(f,x) соответственно.

Для использования пакета fourie его необходимо предварительно загрузить командой load("fourie").

График частичной суммы ряда Фурье для функции f(x) = x, построенной при помощи пакета fourie

увеличить изображение
Рис. 3.23. График частичной суммы ряда Фурье для функции f(x) = x, построенной при помощи пакета fourie

Примеры использования пакета fourie (график полученной функции приведён на рис. 3.23):

(%i1)	load("fourie")$ fourier(x,x,%pi);
(\%t2)\ {a}_{0}=0\\ (\%t3)\ {a}_{n}=0\\ (\%t4)\ {b}_{n}=\frac{2\,\left( \frac{\mathrm{sin}\left( \pi \,n\right) } {{n}^{2}}-\frac{\pi \,\mathrm{cos}\left( \pi \,n\right) }{n}\right) }{\pi }\\ (\%o4)\ [\%t2,\%t3,\%t4]
(%i5)	foursimp(%);
(\%t5)\ {a}_{0}=0\\ (\%t6)\ {a}_{n}=0\\ (\%t7)\ {b}_{n}=-\frac{2\,{\left( -1\right) }^{n}}{n}\\ (\%o7)\ [\%t5,\%t6,\%t7]
(%i8)	fourexpand(%,x,%pi,10);
(\%o8)\ -\frac{\mathrm{sin}\left( 10\,x\right) }{5}+\frac{2\,\mathrm{sin}\left( 9\,x\right) }{9}-\frac{\mathrm{sin}\left( 8\,x\right) }{4}+\frac{2\,\mathrm{sin}\left( 7\,x\right) }{7}-\frac{\mathrm{sin}\left( 6\,x\right) }{3}+\frac{2\,\mathrm{sin}\left( 5\,x\right) }{5}-\frac{\mathrm{sin}\left( 4\,x\right) }{2}+\frac{2\,\mathrm{sin}\left( 3\,x\right) }{3}-\mathrm{sin}\left( 2\,x\right) +2\,\mathrm{sin}\left( x\right)

3.9.8 Дополнительные возможности: обобщённые ряды Фурье

Как указывалось выше, наряду с тригонометрической ортонормированной системой функций достаточно широко используются и другие (в частности, полиномы Лежандра, Чебышёва, Эрмита и др.). Рассмотрим представление функции обобщённым рядом Фурье по полиномам Лежандра.

Вычисление значений ортогональных полиномов в Maxima осуществляется при помощи пакета orthopoly, который позволяет оперировать полиномами Чебышёва, Лежандра, Эрмита, Якоби и др., а также рядом сферических функций.

Интегрируемая на интервале (-1, 1) кусочно-непрерывная функция может быть представлена обобщённым рядом Фурье (в данном случае — по полиномам Лежандра):

f(x)=\sum\limits_{n=0}^{\infty}c_{n}P_{n}(x),
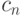где P_n(x) — полином Лежандра степени n, c_n — коэффициенты Фурье для разложения по полиномам Лежандра. Значения c_n вычисляются по формуле:
c_{n}=\frac{2n+1}{2}\int\limits_{-1}^{1}f(x)P_{n}(x)dx.

Пример вычисления разложения функции y = e^x на интервале (-1, 1) в ряд по полиномам Лежандра представлен следующими командами:

(%i1)	load(orthopoly)$ n:5$ f:exp(x)$ l:1$
c(m):=(2*m+1)/2*integrate(f*legendre*p (m, x),x,-l,l)$
z:makelist(k-1, k, 1, n+1)$
cr:makelist(c(z[k]),k,1,n+1)$
fk:makelist(cr[k]*legendre_p (z[k], x),k,1,n+1)$
g:sum(fk[k],k,1,n+1)$
График частичной суммы обобщённого ряда Фурье для функции

увеличить изображение
Рис. 3.24. График частичной суммы обобщённого ряда Фурье для функции

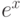График полученного выражения g в сравнении с функцией e^x показан на рис. 3.24.

Как видно из рисунка, графики экспоненты и полученного разложения совпадают. В совпадении результатов можно убедиться, сопоставив выражение g (после упрощения) и разложение экспоненты в ряд Тейлора.

Дальше >>
< Лекция 2 || Лекция 3: 123456789101112131415 || Лекция 4 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 5
Валентин Бирюков
Валентин Бирюков
Россия
предложить дружбу
Далиант Максимус
Далиант Максимус
Украина
предложить дружбу