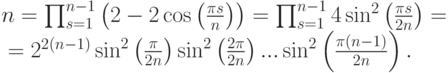НОУ ИНТУИТ | Введение в алгебру. Лекция 6: Комплексные корни n-й степени из единицы и решение уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Аннотация: В данной лекции рассматриваются комплексные корни n-й степени из единицы. Приведены формулы для решения уравнений третьей и четвертой степеней, доказан ряд теорем. Рассмотрен ряд характерных задач, а также приведены задачи для самостоятельного рассмотрения

Ключевые слова: Окружность, доказательство, группа, первообразная, пункт, ПО, дискриминант кубического многочлена, действительный, радиус, значение функции, функция, композиция, минимум, многочлен, многочлен неприводимый, поле, определение, умножение, кратность

Комплексные корни n-й степени из единицы

Так как 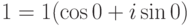$1=1(\cos 0+i\sin 0)$ , r=1, $\varphi=0$ , то формула для корней n -й степени из 1 принимает вид

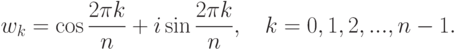
$w_k=\cos \frac{2\pi k}{n}+i\sin\frac{2\pi k}{n},\quad k=0,1,2,...,n-1.$

Точки w_k являются вершинами правильного n -угольника, вписанного в окружность единичного радиуса с центром в начале координат, при этом одной из вершин этого многоугольника является 1. Например, при n=8

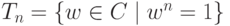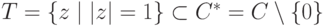Теорема 2.9.1. Совокупность $T_n=\{w\in C\mid w^n=1\}$ всех n корней n -й степени из 1 с операцией умножения является коммутативной группой (подгруппой в $T=\{z\mid |z|=1\}\subset C^*= C\setminus \{0\}$ ).

Доказательство.

Если 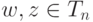$w,z\in T_n$ , т. е. wⁿ=1, zⁿ=1, то 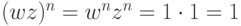$(wz)^n=w^nz^n=1\cdot 1=1$ , поэтому $wz\in T_n$ . Таким образом, на T_n определена операция умножения (очевидно, коммутативная и ассоциативная).
Ясно, что 1ⁿ=1, т. е. 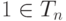$1\in T_n$ , и 1 - нейтральный элемент в T_n.
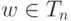Если $w\in T_n$ , то wⁿ=1,
$\left(\frac{1}{w}\right)^n=\frac{1}{w^n}=\frac{1}{1}=1,$
и поэтому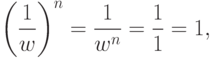 $w^{-1}\in T_n$ .

Замечание 2.9.2. Группа T_n является циклической, т. е. все ее элементы являются степенями одного элемента, называемого циклическим образующим (в качестве одного из циклических образующих можно взять $w_1=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}$ , так как w_k=(w₁)^k для $0 \leq k \leq n-1$ , т. е. все элементы w_k группы T_n являются степенями корня w₁, такие корни называются первообразными). 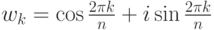Покажите, что $w_k=\cos\frac{2\pi k}{n}+i\sin\frac{2\pi k}{n}$ является первообразным корнем тогда и только тогда, когда наибольший общий делитель чисел k и n равен 1.

Упражнение 2.9.3. Доказать, что сумма всех k -х степеней корней уравнения xⁿ=1 равна

n, если k делится на n ;

0, если k не делится на n.

Задача 2.9.4. Если 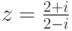$z=\frac{2+i}{2-i}$ , то |z|=1, но z не является корнем из единицы (т. е. 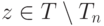$z\in T\setminus T_n$ для любого $n\in N$ ).

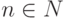Задача 2.9.5. Доказать, что

а) 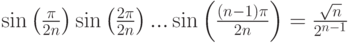$\sin\left(\frac{\pi}{2n}\right)\sin\left(\frac{2\pi}{2n}\right)... \sin\left(\frac{(n-1)\pi}{2n}\right)=\frac{\sqrt{n}}{2^{n-1}}$ ;

б) 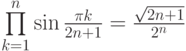$\prod\limits_{k=1}^n \sin\frac{\pi k}{2n+1}=\frac{\sqrt{2n+1}}{2^n}$ .

Указание. Пусть

$x_s=\varepsilon_s=\cos\frac{\pi s}{n}+i\sin\frac{\pi s}{n},\quad s=1,2,...,2n$

(все корни степени 2n из 1 ).Тогда

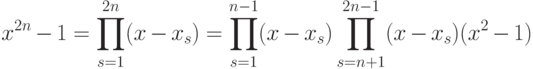
$x^{2n}-1=\prod\limits_{s=1}^{2n}(x-x_s)= \prod_{s=1}^{n-1}(x-x_s)\prod_{s=n+1}^{2n-1}(x-x_s)(x^2-1)$

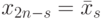(так как x_n=-1, x_2n=1 ). Но $x_{2n-s}=\bar x_s$ , поэтому

$\begin{mult} x^{2n}-1=(x^2-1)\smash[b]{\prod_{s=1}^{n-1}(x-x_s)(x-\bar x_s)}={}\\ {}=(x^2-1)\prod_{s=1}^{n-1}\left(x^2-2x\cos\frac{\pi s}{n}+1\right). \end{multl}$

Следовательно,

$\frac{x^{2n}\!-\!1}{x^2\!-\!1}= x^{2(n-1)}+x^{2(n-2)}+...+x^2+1= \prod_{s=1}^{n-1}\!\left(x^2-2x\cos\frac{\pi s}{n}\!+\!1\right).$

Полагая x=1, имеем

$\begin{mult} n=\prod_{s=1}^{n-1}\left(2-2\cos\left(\frac{\pi s}{n}\right)\right)= \prod_{s=1}^{n-1}4\sin^2\left(\frac{\pi s}{2n}\right)={}\\ {}=2^{2(n-1)}\sin^2\left(\frac{\pi}{2n}\right) \sin^2\left(\frac{2\pi}{2n}\right)... \sin^2\left(\frac{\pi(n-1)}{2n}\right). \end{mult}$

Пункт б) доказывается аналогично.

Дальше >>

Введение в алгебру

Введение в алгебру

Комплексные корни n-й степени из единицы и решение уравнений

Комплексные корни n-й степени из единицы

Вопросы и ответы

Студенты

Авторизоваться

Введение в алгебру

Введение в алгебру

Комплексные корни n-й степени из единицы и решение уравнений

Комплексные корни n-й степени из единицы

Вопросы и ответы

Студенты