НОУ ИНТУИТ | Введение в алгебру. Лекция 6: Комплексные корни n-й степени из единицы и решение уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Решение уравнений третьей и четвертой степени

Любое уравнение

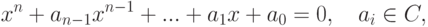
$x^n+a_{n-1}x^{n-1}+...+a_1x+a_0=0,\quad a_i\in C,$

с помощью замены

$x=y-\frac{a_{n-1}}{n}$

(если $a_{n-1}\neq 0$ ) сводится к уравнению

$y^n+b_{n-2}y^{n-2}+...+b_1y+b_0=0,\quad b_i\in C.$

Упражнение 2.10.1 (решение уравнений третьей степени, формула Кардано). Покажите, что для n=3 все решения кубического уравнения x³+px+q=0 ( 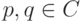$p,q\in C$ ) имеют вид u+v, где $uv=\smash[b]{-\frac{p}{3}}$ , u³ и v³ - корни квадратного уравнения $z^2+qz-\frac{p^3}{27}=0$ . Таким образом, для всех трех решений имеем формулу Кардано

$x=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+ \sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}},$

где кубические корни u и v связаны соотношением $uv=\smash[b]{-\frac{p}{3}}$ .

Если u₁ и v₁ - какие-либо значения корней

$\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\quad\text{и}\quad \sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$

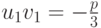соответственно и $u_1v_1=-\frac{p}{3}$ , то корни находятся по правилу

$x_1=u_1+v_1,\quad x_2=u_1\omega+v_1\omega^2,\quad x_3=u_1\omega^2+v_1\omega,$

где $\omega=-\frac{1}{2}+\frac{\sqrt{3}}{2}i=\sqrt[3]{1}$ .

Величина D=-27q²-4p³ называется дискриминантом многочлена x³+px+q . Условие D=0 равносильно существованию кратного корня (при D=0 и $p\neq 0$ имеем $x_1=\frac{3q}{p}$ , $x_2=x_3=-\frac{3q}{2p}$ , при этом если $\smash[t]{\frac{3q}{p}=-\frac{3q}{2p}}$ , то имеется корень кратности 3 ; если D=0 и p=0, то q=0, а уравнение принимает вид x³=0 ).

Если $p,q\in R$ , то: при D>0 имеется три различных действительных корня; при D<0 имеется один действительный и два мнимых сопряженных корня; при D=0 все корни действительные, из них хотя бы два совпадают.

Примеры 2.10.2.

x³+5x²+2x-8=0, x₁=1, x₂=-2, x₃=-4.
x³-6ix+4(1-i)=0, x₁=-1-i, x₂=-1-i, x₃=2+2i.
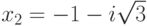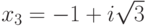x³+9x²+18x+28=0, x₁=-7, $x_2=-1-i\sqrt{3}$ , $x_3=-1+i\sqrt{3}$ .

Упражнение 2.10.3 (решение уравнений четвертой степени; Феррари, Эйлер). Для решения уравнения

$x^4+px^2+qx+r=0\quad (p,q,r\in C)$

рассматривается соответствующее кубическое уравнение y³+2py²+(p²-4r)y-q²=0. Если y₁, y₂, y₃ - корни этого уравнения, то все корни исходного уравнения находятся по правилу

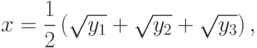
$x=\frac{1}{2}\left(\sqrt{y_1}+\sqrt{y_2}+\sqrt{y_3}\right),$

где выбор квадратных корней подчинен условию

$\sqrt{y_1}\sqrt{y_2}\sqrt{y_3}=-q.$

Задача 2.10.4. Решить уравнения

x⁴+2x³+x²-1=0,

Ответ: $-\frac{1}{2}(1\pm\sqrt{5})$ , $-\frac{1}{2}(1\pm i\sqrt{3})$ ;

x⁴+2x³+2x²+x-7=0,

Ответ: $-\frac{1}{2}\left(1\pm i\sqrt{2\sqrt{29}+1}\right)$ , $-\frac{1}{2}\left(1\pm \sqrt{2\sqrt{29}-1}\right)$ .

Замечание 2.10.5. Отметим, что общее уравнение пятой степени неразрешимо в радикалах, при этом существует критерий разрешимости в радикалах уравнения любой степени (Абель, Галуа).

Дальше >>

Введение в алгебру

Введение в алгебру

Комплексные корни n-й степени из единицы и решение уравнений

Решение уравнений третьей и четвертой степени

Вопросы и ответы

Студенты

Авторизоваться

Введение в алгебру

Введение в алгебру

Комплексные корни n-й степени из единицы и решение уравнений

Решение уравнений третьей и четвертой степени

Вопросы и ответы

Студенты