Комплексные корни n-й степени из единицы и решение уравнений
Основная теорема алгебры комплексных чисел (теорема Гаусса, 1799 г.)
Теорема 2.11.1. Если ![f(x)\in C[x]](/sites/default/files/tex_cache/e571bb6b84bf145986c73c2c5367ae74.png) ,
, 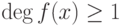 , то существует корень
, то существует корень 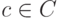 многочлена f(x), т. е. f(c)=0.
многочлена f(x), т. е. f(c)=0.
Шаг 1 (существование абсолютного минимума вещественнозначной функции |f(x)| на комплексных числах C ). Напомним, что |z1z2|=|z1|,|z2| и
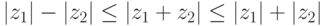
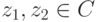 .
.Лемма 2.11.2. Если f(x)=xn+an-1xn-1+...+a1x+a0, 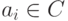 ,
,  , то найдется радиус
, то найдется радиус 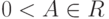 такой, что
такой, что

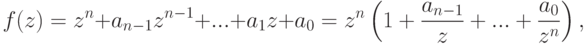
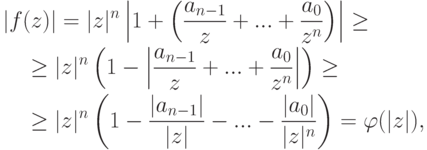

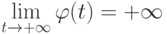 , и поэтому для любого C (например, для C=|f(0)|=|a0| ) найдется
, и поэтому для любого C (например, для C=|f(0)|=|a0| ) найдется 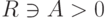 такое, что для t>A имеем
такое, что для t>A имеем 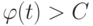 . Итак, если |z|=t>A, то
. Итак, если |z|=t>A, то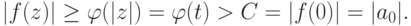
Так как функция 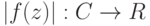 непрерывна как композиция двух непрерывных функций
непрерывна как композиция двух непрерывных функций 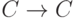 ,
, 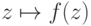 ,
,  ,
,  (или если z=u+vi,
(или если z=u+vi, 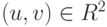 , то
, то 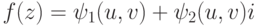 , где
, где 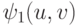 и
и 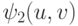 - многочлены с действительными коэффициентами от u, v, и поэтому
- многочлены с действительными коэффициентами от u, v, и поэтому 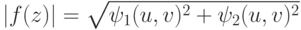 - непрерывная функция от (u,v) ), то на замкнутом ограниченном множестве (компакте)
- непрерывная функция от (u,v) ), то на замкнутом ограниченном множестве (компакте)
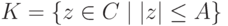
 . В частности,
. В частности, 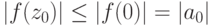 . Если
. Если 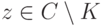 , т. е. |z|>A, то, как мы видели,
, т. е. |z|>A, то, как мы видели,
Шаг 2. Мы покажем, что f(z0)=0, т. е. c=z0 является корнем многочлена f(x). Действительно, если 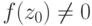 , то |f(z0)|>0 и, как показывает следующая лемма Даламбера, это допущение противоречит тому, что z_0 - абсолютный минимум функции |f(x)|.
, то |f(z0)|>0 и, как показывает следующая лемма Даламбера, это допущение противоречит тому, что z_0 - абсолютный минимум функции |f(x)|.
Лемма 2.11.3 (лемма Даламбера). Пусть ![f(x)\in C[x]](/sites/default/files/tex_cache/e571bb6b84bf145986c73c2c5367ae74.png) ,
, 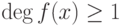 ,
, 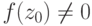 для
для 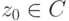 . Тогда для любого
. Тогда для любого 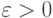 найдется такой элемент
найдется такой элемент 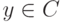 , что
, что  и |f(z0+y)|<|f(z0)|.
и |f(z0+y)|<|f(z0)|.
Доказательство. Если z=z0+y, т. е. y=z-z0, то f(z)=a0+a1z+...+an-1zn-1+zn=
=c0+c1y+...+cn-1yn-1+cnyn,
где  (при y=0 имеем z=z0 ), cn=1 (как коэффициент при yn в (z0+y)n ).
(при y=0 имеем z=z0 ), cn=1 (как коэффициент при yn в (z0+y)n ).
Пусть k>0 - наименьший номер слагаемого, для которого 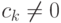 . Итак, f(z)=c0+ckyk+ck+1yk+1+...+cnyn.
Основное соображение заключается в том, что в окрестности точки z0 (т. е. y=0 ) поведение многочлена определяется первыми двумя членами c0+ckyk.
. Итак, f(z)=c0+ckyk+ck+1yk+1+...+cnyn.
Основное соображение заключается в том, что в окрестности точки z0 (т. е. y=0 ) поведение многочлена определяется первыми двумя членами c0+ckyk.
Сначала пусть y0 - одно из решений уравнения c0+ckyk=0 (т. е.  , y0 - один из k корней из комплексного числа
, y0 - один из k корней из комплексного числа 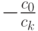 ). Если, далее,
). Если, далее, 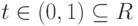 , то
, то  , и поэтому
, и поэтому
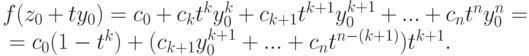
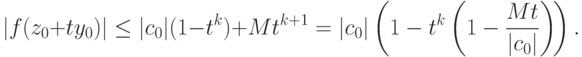
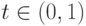 достаточно малым, так что Mt<|c0|,
достаточно малым, так что Mt<|c0|, 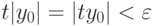 . Тогда
. Тогда 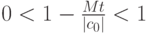 , и поэтому
, и поэтому
Теорема 2.11.4 (о разложении многочлена с комплексными коэффициентами в произведение линейных множителей). Пусть ![f(x)\in C[x]](/sites/default/files/tex_cache/e571bb6b84bf145986c73c2c5367ae74.png) ,
, 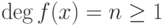 . Тогда
. Тогда

Доказательство. В силу теоремы Гаусса найдется такое 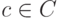 , что f(c)=0. По теореме Безу
, что f(c)=0. По теореме Безу
![f(x)=(x-c)q(x),\quad q(x)\in C[x],\ \ \deg q(x)=n-1.](/sites/default/files/tex_cache/3d3c68f2e24ba786816ae4ca1b266a3a.png)
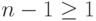 . Продолжая этот процесс, убеждаемся в существовании разложения на линейные множители.
. Продолжая этот процесс, убеждаемся в существовании разложения на линейные множители.Пусть теперь
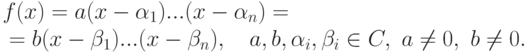
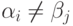 для всех j=1,...,n, то
для всех j=1,...,n, то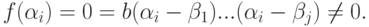

 , получаем
, получаем  , и поэтому
, и поэтому 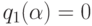 , что противоречит
, что противоречит 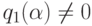 .
.Следствие 2.11.5. Если  - различные корни многочлена
- различные корни многочлена ![f(x)\in C[x]](/sites/default/files/tex_cache/e571bb6b84bf145986c73c2c5367ae74.png) , k1,...,kr - их кратности,
, k1,...,kr - их кратности,  , то n=k1+...+kn )таким образом, многочлен степени
, то n=k1+...+kn )таким образом, многочлен степени  имеет ровно n корней с учетом их кратности ).
имеет ровно n корней с учетом их кратности ).
Замечание 2.11.6 (о неприводимых многочленах над полем комплексных чисел). По аналогии с определением простых чисел в кольце целых чисел Z многочлен ![f(x)\in K[x]](/sites/default/files/tex_cache/cc2b444b908aa370fabb8e7c785249e3.png) ,
, 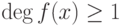 , называется неприводимым, если f(x) нельзя представить в виде
, называется неприводимым, если f(x) нельзя представить в виде 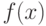 ,
, 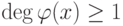 ,
, 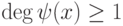 (иными словами, если
(иными словами, если 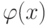 - делитель многочлена f(x),
- делитель многочлена f(x), 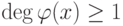 , то
, то 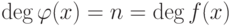 ).
).
Таким образом, мы установили, что неприводимые многочлены над полем C комплексных чисел - это в точности многочлены первой степени. Из единственности разложения на линейные множители над C получаем существование и единственность разложения на неприводимые многочлены над C.
Лемма 2.11.7.Если K - поле, ![f(x),g(x)\in K[x]](/sites/default/files/tex_cache/ddd4932a70b8b625db7b0223ceeeb78d.png) ,
, 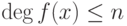 ,
,  , f(x) и g(x) совпадает в (n+1) -й различных точках
, f(x) и g(x) совпадает в (n+1) -й различных точках 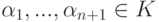 , то f(x)=g(x).
, то f(x)=g(x).
Доказательство. Пусть h(x)=f(x)-g(x). Тогда если  , то
, то 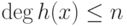 и
и 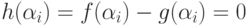 для i=1,...,n+1. Но это противоречит тому, что число различных корней не превосходит степени многочлена.
для i=1,...,n+1. Но это противоречит тому, что число различных корней не превосходит степени многочлена.
Следствие 2.11.8. Если  )в частности,для K= Q, R или C ), то формальное и функциональное определение равенства многочленов совпадают.
)в частности,для K= Q, R или C ), то формальное и функциональное определение равенства многочленов совпадают.
Замечание 2.11.9. Для конечного поля Z2 разные многочлены x и x2 в точках 0 и 1 принимают одинаковые значения, т. е. равны как функции их Z2 в Z2.
Теорема 2.11.10 (формулы Виета). Если K - поле, 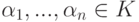 ,
,

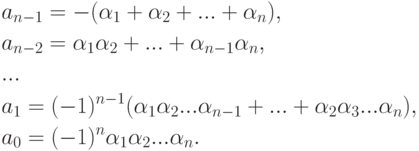
Доказательство. В силу закона дистрибутивности умножение на  сводится к умножениям на x и на
сводится к умножениям на x и на 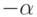 . Формулы Виета получаются подсчетом коэффициента при xk (т. е. надо при указанных раскрытиях скобок k раз выбрать x и, следовательно, (n-k) раз корни).
. Формулы Виета получаются подсчетом коэффициента при xk (т. е. надо при указанных раскрытиях скобок k раз выбрать x и, следовательно, (n-k) раз корни).
Упражнение 2.11.11. Пусть сумма корней многочлена с комплексными коэффициентами (считая кратность) равна нулю. Докажите, что сумма корней производной этого многочлена также равна нулю.
Упражнение 2.11.11. Пусть x1,...,xn - корни многочлена ![1+x+x^2+...+x^n\in C[x]](/sites/default/files/tex_cache/4c43ce39029f07132c8e6a11540492f3.png) . Тогда:
. Тогда:
- многочлен (1+x)n+1-xn+1 имеет корни
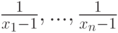 ;
; -
![\smash[t]{\frac{1}{x_1-1}+\frac{1}{x_2-1}+...+\frac{1}{x_n-1}=-\frac{n}{2}}](/sites/default/files/tex_cache/6aa97e390f6be14250c452a410d6c0ea.png) .
.


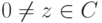 . Тогда
. Тогда