Алгоритмы проектирования проводных и печатных соединений (методы трассировки)
21.4. Трассировка печатного (пленочного) монтажа
Волновой алгоритм трассировки его модификации
Многие методы трассировки печатных соединений основаны на идеях волнового алгоритма, предложенного Ли. Последний представляет собой развитие алгоритмов построения кратчайших путей в сети и позволяет находить маршруты соединений, оптимальные по ряду параметров.
Основные положения
КП разбивается на элементарные ячейки. Размеры ячеек и их количество определяются:
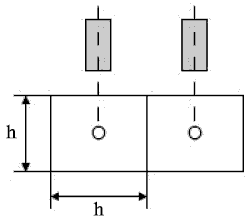
Выбранная система ячеек определяет среду, в которой осуществляется построение соединений. В простейшем случае ячейка представляет собой квадрат со стороной " h ", равной расстоянию между средними линиями двух соседних печатных проводников (рис. 21.3).
Если размеры поля по горизонтали и вертикали, соответственно, 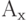 и
и 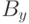 ,
то получим дискретное рабочее поле (ДРП) с
,
то получим дискретное рабочее поле (ДРП) с  ячейками
ячейками
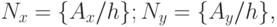
где  и
и 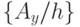 - символы ближайшего большего целого.
- символы ближайшего большего целого.
Так формируется дискретное рабочее поле (ДРП).
В данном ДРП определяется множество занятых ячеек, соответствующее зонам, запрещённым для проведения соединений: выводы элементов, технологические области, ранее проведённые соединения и прочее. По мере проведения соединений множества занятых и свободных ячеек изменяются.
Основу всех модификаций алгоритма Ли составляет процедура построения оптимального в заданном смысле пути между двумя известными ячейками ДРП. Процедура состоит из двух этапов: поиска пути и проведения пути.
На первом этапе из одной из заданных ячеек ДРП - источника моделируется распространение числовой волны до тех пор, пока её фронт не достигнет второй отмеченной ячейки ДРП. В первом случае искомый путь существует, во втором - нет.
Все условия, которые необходимо выполнить, при проведении соединения, в том числе и условия оптимальности, должны быть заложены в правила движения волны, т.е. в правила построения её очередного фронта. В процессе распространения волны ячейкам ДРП присваиваются весовые оценки, связанные с принятым критерием оптимальности.
На втором этапе алгоритма осуществляется проведение пути. Для этого следует, начиная от ячейки - цели, двигаться в направлении, противоположном направлению распространения волны, переходя последовательно от ячейки с большим весом к соседней ячейке с меньшим весом до тех пор, пока не будет достигнута ячейка - источник. Ячейки ДРП, выделенные в ходе указанного процесса, и определяют искомую оптимальную трассу.
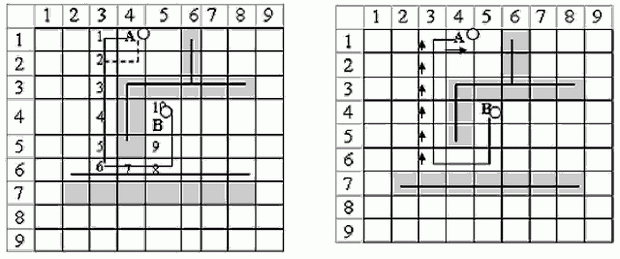
Использование путевых координат при распространении волны позволяет исключить вычисления и хранение весов ячеек ДРП (рис. 21.4,а).
Назначение путевой координаты ячейке  в случае, если имеется несколько соседних ячеек фронта
в случае, если имеется несколько соседних ячеек фронта 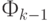 производится согласно выбранному правилу приоритетов.
Например:
производится согласно выбранному правилу приоритетов.
Например:  . Этап проведения пути состоит в отслеживании путевых координат в размеченном ДРП, начиная от ячейки - цели (рис. 21.5, б).
. Этап проведения пути состоит в отслеживании путевых координат в размеченном ДРП, начиная от ячейки - цели (рис. 21.5, б).
В методе путевых координат ячейка ДРП может быть в одном из следующих состояний: пустая, занятая или содержать координату:
На основании этой последовательности выделяется искомый путь в ДРП. В неопределённых ситуациях, также как и в основной схеме алгоритма, должно быть использовано некоторое правило приоритетов.
Рассмотренный выше вариант волнового алгоритма может быть использован для трассировки однослойных соединений, когда пересечения между отдельными проводниками запрещены.
Трассировка по магистралям
Волновой алгоритм в той или иной модификации является основой большинства развитых программ машинной трассировки ввиду его универсальности.
Однако в определённых ситуациях эффективнее применять другие алгоритмы, которые дают более быстрое и качественное решение.
Алгоритмы построения соединений с малым числом поворотов (лучевой алгоритм).Это такой алгоритм трассировки, в котором основные процедуры поиска и проведения пути осуществляются путём исследования пространства магистралей (линий), а не ячеек ДРП, как в классическом алгоритме Ли.
Для построения процесса рассмотрим ДРП (рис. 21.5).
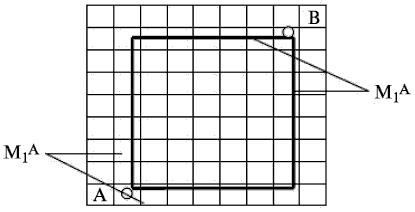
Пусть, требуется найти соединение между точками А и В. Построим из точек А и В лучи в горизонтальном и вертикальном направлениях, используя лишь свободные ячейки поля.
Будем считать их магистралями первого уровня (фронта) и обозначим их, соответственно, 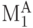 и
и 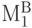 .
.
В простейшем случае, когда эти магистрали пересекутся, сразу получаем искомое соединение.
При использовании алгоритма Ли для построения этого же пути пришлось бы последовательно рассмотреть состояние всех ячеек, по крайней мере, входящих в прямоугольник, содержащий ячейки А и В.
Если магистрали 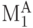 и
и 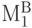 не пересекаются, строим магистрали второго уровня (фронта).
Соответственно, для точек
не пересекаются, строим магистрали второго уровня (фронта).
Соответственно, для точек  и
и  (рис. 21.6).
(рис. 21.6).
На рис. 21.6 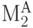 и
и 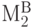 - магистрали второго уровня.
- магистрали второго уровня.
Эти магистрали перпендикулярны к магистралям первого уровня и проводятся через точки, расположенные в узлах основной сетки. Назовём эти точки базовыми.
При переходе с магистралей первого уровня на магистрали второго уровня в возможную конфигурацию соединения добавляется один поворот.
Использование алгоритма трассировки по магистралям приводит к минимизации числа переходов при трассировке двухслойных схем с ортогональными соединениями. Такие пути называются простейшими или малоповоротными.
В общем случае процесс построения магистралей  -го уровня состоит в выборе базовых точек на магистралях i - го уровня и проведении через них отрезков нормалей, не пересекающих области, запрещённые для проведения соединений.
-го уровня состоит в выборе базовых точек на магистралях i - го уровня и проведении через них отрезков нормалей, не пересекающих области, запрещённые для проведения соединений.
Построение магистралей каждого следующего уровня выполняется попеременно, например, для точек  и
и 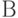 до тех пор, пока либо очередной уровень не может быть образован (проведение пути невозможно),
либо на очередном шаге некоторая магистраль из
до тех пор, пока либо очередной уровень не может быть образован (проведение пути невозможно),
либо на очередном шаге некоторая магистраль из 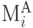 пересечётся с магистралью из
пересечётся с магистралью из 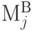 .
.
В последнем случае может быть построен путь, содержащий 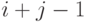 поворот (переход).
поворот (переход).
Для минимизации длины пути применяется следующая процедура.
Пусть, магистраль уровня  точки
точки  пересекла несколько магистралей уровня
пересекла несколько магистралей уровня  точки
точки  .
Тогда выбирается сначала наименьший отрезок магистрали
.
Тогда выбирается сначала наименьший отрезок магистрали 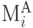 , обеспечивающей пересечения с одной из магистралей
, обеспечивающей пересечения с одной из магистралей 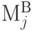 , далее - наименьший отрезок из
, далее - наименьший отрезок из  , обеспечивающий соединение с выбранным отрезком
, обеспечивающий соединение с выбранным отрезком  -го уровня,
и т.д., до достижения точки
-го уровня,
и т.д., до достижения точки  .
.
Аналогичная процедура применяется для магистралей всех уровней точки В.
Результирующий путь  состоит из выбранных отрезков и содержит минимальное число поворотов.
состоит из выбранных отрезков и содержит минимальное число поворотов.
Рассмотренный принцип трассировки по магистралям с незначительной модификацией может быть использован для построения многоконцевых соединений.
Следует отметить, что при программной реализации алгоритма на ЭВМ можно отказаться от матричного способа кодировании КП. Поэтому время работы алгоритма и требуемый объём памяти не зависят прямым образом от размеров КП, а определяются, главным образом, сложностью конфигураций уже приложенных соединений. В связи с этим трассировка по магистралям с точки зрения затрат времени и памяти ЭВМ более эффективна, чем волновой алгоритм, для полей большой площади, причём требуемые затраты времени существенно меньше для слабо заполненных полей. По мере заполнения поля трассами соединений эффективность процесса поиска снижается и временные затраты ЭВМ приближаются к затратам времени волнового алгоритма.
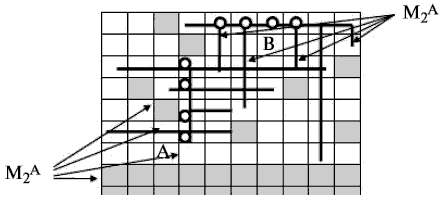
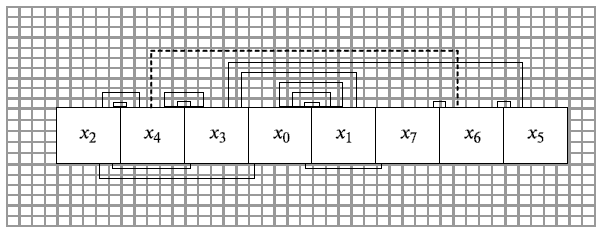
Осуществим трассировку схемы с использованием волнового и лучевого алгоритмов (рис. 21.7).
Итак, в ходе трассировки монтажных соединений заданной схемы была решена задача геометрического построения на коммутационном поле всех цепей конструкции. Однако исключить все пересечения не удалось. Использовать двухслойный монтаж для этой схемы не имеет смысла, так как он будет очень объёмным и дорогостоящим при больших объёмах производства. Целесообразнее показанное пунктиром соединение сделать проводным, впаяв перемычку в отверстия с контактными площадками. Или, применяя более современную базу, над соединяющей элементы 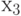 и
и  дорожкой припаять безвыводную перемычку.
дорожкой припаять безвыводную перемычку.
Рассмотренные алгоритмы показывают эффективность их комплексного использования в зависимости от конкретных условий.