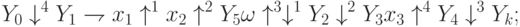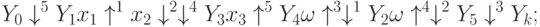НОУ ИНТУИТ | Введение в теорию автоматов. Лекция 3: Способы описания работы дискретных устройств

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2008 | Уровень: специалист | Доступ: свободно | ВУЗ: Вятский государственный университет

|

Вам нравится? Нравится 30 студентам

| Поделиться |

Поддержать программу

3.5 Логические схемы алгоритмов

Основное достоинство рассматриваемых ниже логических схем алгоритмов (ЛСА) состоит в том, что, являясь по существу разновидностью языка операторных схем, они допускают запись алгоритма в строчку, что часто является удобным, т.к. появляется возможность исключить процесс рисования, вычерчивания, как это имеет место в ГСА. Важным является также наличие развитой системы преобразований ЛСА и возможности формального перехода к автоматному отображению.

Основными элементами ЛСА являются так же, как и в ГСА, операторы и логические условия.

Основные отличия от ГСА состоят в том, что для указания взаимосвязей между операторами и логическими условиями используются верхние и нижние стрелки.

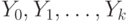Логической схемой алгоритма называется строчка, составленная из символов операторов $А_0,А_1,\dots,А_n,A_k$ , или $Y_0, Y_1,\dots,Y_k$ и логических условий 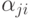$\alpha_{ji}$ , а также верхних и нижних стрелок. Иногда верхние и нижние стрелки заменяют на правые и левые полускобки.

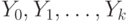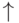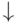Итак, ЛСА- строчка, составленная из символов операторов $Y_0, Y_1,\dots,Y_k$ , логических условий и верхних $\uparrow$ и нижних $\downarrow$ стрелок, причем:

Сильная операторная вершина 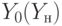и одна конечная ;
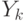Строка начинается с 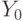и заканчивается ;
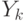Не должно быть двух нижних стрелок $\downarrow$ с одинаковыми номерами;
Для каждой нижней стрелки $\downarrow$ должна быть по крайней мере одна верхняя;

Переход по логическому условию X_i , стоящему в ЛСА

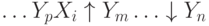
$\dots Y_p X_i \uparrow Y_m \dots \downarrow Y_n$

осуществляется так:

Если 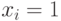, то после 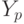выполнится ,
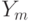Если 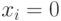, то после 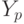выполнится .

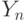Безусловный переход для ясности может быть обозначен дополнительным символом, например 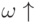$\omega \uparrow$ .

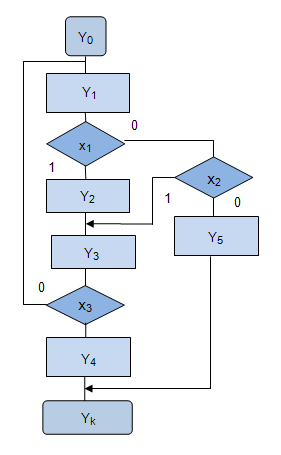
ЛСА для МП, представленной на рис. 3.7 выглядит так:

$A_0 \downarrow^3A_1p_1\uparrow^1A_3 p_2\uparrow^2 \omega \uparrow^3 \downarrow ^1A_2 \downarrow ^2A_k.$

Правило чтения ЛСА состоит в следующем.

Вначале анализируется элемент ЛСА, следующий непосредственно за оператором 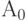А_0 . Если рассматриваемым элементом является оператор, то он отмечается (выписывается) и на следующем шаге анализируется стоящий справа элемент (оператор или логическое условие).

Если рассматриваемым элементом является логическое условие 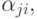$\alpha_{ji},$ производится проверка этого условия;

Анализ ЛСА при соблюдении сформулированных правил приводит через некоторое количество шагов к получению строчки операторов, называемой значением ЛСА при заданной последовательности наборов логических условий.

Пусть задана ЛСА.

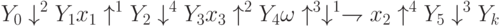
$Y_0 \downarrow^2Y_1 x_1 \uparrow^1Y_2 \downarrow^4Y_3 x_3 \uparrow^2Y_4 \omega \uparrow^3\downarrow^1\rightharpoondown x_2 \uparrow^4 Y_5 \downarrow^3Y_k$

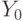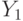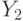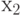Построим соответствующую ей ГСА. За начальным оператором Y_0 следует оператор Y_1 и далее логическое условие x_1 . Если логическое условие выполняется, то есть x_1=1 , то следующим оператором выполняется Y_2 . Если логическое условие не выполняется, то есть x_1=0 , то следующим оператором выполняется х_2 , то есть оператор, стоящий за нижней стрелкой с номером 1.

Далее в ЛСА за оператором 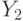Y_2 стоит оператор 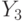Y_3 и x_3 . В такой последовательности и изображаем их на ГСА. Далее строим аналогичным образом.

Одной важной особенностью ЛСА является возможность неоднозначной записи одного и того же алгоритма.

Рис. 3.8.

Так, ГСА на рис.3.8 может быть описана еще несколькими вариантами ЛСА:

$Y_0 \downarrow^4Y_1 \rightharpoondown x_1 \uparrow^1 x_2 \uparrow^2Y_5 \omega \uparrow^3 \downarrow^1Y_2 \downarrow^2Y_3 x_3\uparrow^ 4Y_4 \downarrow ^3Y_k;$

$Y_0 \downarrow^5Y_1 x_1\uparrow^1 x_2\downarrow^2 \downarrow^4 Y_3 x_3\uparrow^5Y_4 \omega \uparrow^3 \downarrow^1Y_2 \omega \uparrow^4 \downarrow^2 Y_5 \downarrow^3Y_k;$

Дальше >>

Авторизоваться

Введение в теорию автоматов

Способы описания работы дискретных устройств

3.5 Логические схемы алгоритмов

Вопросы и ответы