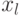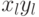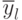|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
На практике часто ограничиваются обобщенными оценками адекватности построенной модели: величиной среднего абсолютного отклонения
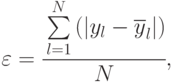
или (и) величиной среднеквадратической ошибки на единицу веса
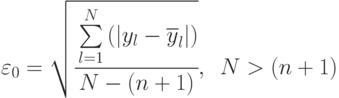
Весом или степенью свободы эксперимента называют разность 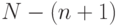 между числом наблюдений
между числом наблюдений  и числом коэффициентов регрессии
и числом коэффициентов регрессии 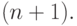
Предположим, что линейная модель 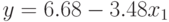 недостаточно точно отображает связь между фактором
недостаточно точно отображает связь между фактором  и откликом
и откликом 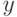 .
.
Введем в рассмотрение более сложную нелинейную модель:
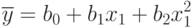
Для определения коэффициентов регрессии 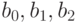 обозначим
обозначим  и получим двухфакторную линейную модель:
и получим двухфакторную линейную модель:
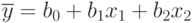
В этом случае уравнение (5.3) раскрывается так:
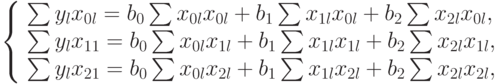
В уравнениях принято: 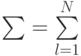
Так как 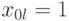 ,
,  , то система принимает вид:
, то система принимает вид:
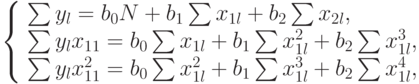
Подставим значения фактора и отклика из табл. 5.10:

Решим систему из трех уравнений с тремя неизвестными и получим: 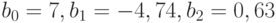 .
.
Таким образом, получено новое уравнение регрессии:
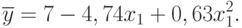
По значениям 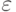 и
и 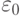 нетрудно убедиться в том, что нелинейная модель более точно отображает моделируемый процесс (см. табл. 5.10), чем линейная.
нетрудно убедиться в том, что нелинейная модель более точно отображает моделируемый процесс (см. табл. 5.10), чем линейная.
В рассмотренном примере ошибка модели определялась по тем же данным, по которым и была определена сама модель. Однако при сокращенных планах экспериментов (см. п. 4.3) можно выполнить все или часть "сэкономленных" наблюдений для получения так называемых проверочных данных, которые и использовать для вычисления ошибки 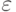 или
или 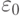 . В этом случае оценка адекватности модели будет более объективна, хотя число наблюдений в эксперименте увеличивается, и экономии их не будет.
. В этом случае оценка адекватности модели будет более объективна, хотя число наблюдений в эксперименте увеличивается, и экономии их не будет.
По уравнению регрессии можно сделать ориентировочную оценку чувствительности отклика к изменению того или иного фактора. Например, в уравнении 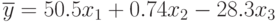 влияние фактора
влияние фактора  на отклик незначительно по сравнению с другими, так как коэффициент
на отклик незначительно по сравнению с другими, так как коэффициент 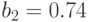 намного меньше остальных коэффициентов.
намного меньше остальных коэффициентов.
В программном пакете MS Excel есть функция "Регрессия", которая может выполнить всесторонний регрессионный анализ данных компьютерного эксперимента.
Пример 5.9. В ремонтное подразделение поступают вышедшие из строя средства связи (СС) с интервалами времени, подчиненными показательному закону с математическим ожиданием  . В каждом СС могут быть неисправными в любом сочетании блоки A, B, C с вероятностями
. В каждом СС могут быть неисправными в любом сочетании блоки A, B, C с вероятностями 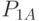 ,
,  ,
, 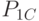 соответственно. Ремонтное подразделение ремонтирует СС путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС в ремонтное подразделение вероятности наличия в нем исправных блоков
соответственно. Ремонтное подразделение ремонтирует СС путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС в ремонтное подразделение вероятности наличия в нем исправных блоков 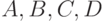 соответственно
соответственно  . Наличие и замена блока
. Наличие и замена блока 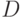 обязательно при любом сочетании неисправных блоков.
обязательно при любом сочетании неисправных блоков.
Построить имитационную модель "Система ремонта" с целью определения вероятности ремонта СС с неисправными блоками  ,
, 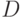 и
и  ,
,  ,
, 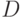 за время
за время  . По результатам эксперимента получить уравнение регрессии, связывающее вероятность ремонта СС с вероятностями
. По результатам эксперимента получить уравнение регрессии, связывающее вероятность ремонта СС с вероятностями 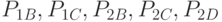 .
.
Решение
Постановка примера 5.9 аналогична постановке примера 3.8. Отличие состоит в том, что введен фактор времени - интервалы поступления неисправных СС. Это учтено в модели, при разработке которой использовался алгоритм примера 3.8 (см. рис. 3.18).
Для построения уравнения регрессии введем обозначения:
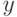 - отклик модели, вероятность ремонта СС с неисправными блоками
- отклик модели, вероятность ремонта СС с неисправными блоками  и
и 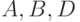 за время
за время  ;
;
 - фактор, представляющий вероятность
- фактор, представляющий вероятность 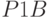 ;
;
 - фактор, представляющий вероятность
- фактор, представляющий вероятность 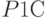 ;
;
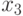 - фактор, представляющий вероятность
- фактор, представляющий вероятность 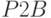 ;
;
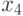 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
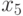 - фактор, представляющий вероятность
- фактор, представляющий вероятность 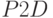 .
.
Исходные данные и результаты эксперимента с моделью в количестве 32 наблюдений приведены в табл. 5.12. По этим данным функция "Регрессия" из MS Excel сформировала искомое уравнение:
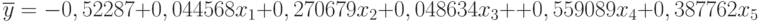
| № отклика | 
|
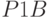
|
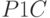
|
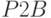
|
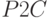
|
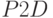
|
|---|---|---|---|---|---|---|
| 1 | 0,088 | 0,3 | 0,55 | 0,5 | 0,2 | 0,65 |
| 2 | 0,127 | 0,3 | 0,55 | 0,5 | 0,2 | 0,95 |
| 3 | 0,303 | 0,3 | 0,55 | 0,5 | 0,8 | 0,65 |
| 4 | 0,442 | 0,3 | 0,55 | 0,5 | 0,8 | 0,95 |
| 5 | 0,099 | 0,3 | 0,55 | 0,9 | 0,2 | 0,65 |
| 6 | 0,146 | 0,3 | 0,55 | 0,9 | 0,2 | 0,95 |
| 7 | 0,317 | 0,3 | 0,55 | 0,9 | 0,8 | 0,65 |
| 8 | 0,46 | 0,3 | 0,55 | 0,9 | 0,8 | 0,95 |
| 9 | 0,116 | 0,3 | 0,85 | 0,5 | 0,2 | 0,65 |
| 10 | 0,167 | 0,3 | 0,85 | 0,5 | 0,2 | 0,95 |
| 11 | 0,445 | 0,3 | 0,85 | 0,5 | 0,8 | 0,65 |
| 12 | 0,653 | 0,3 | 0,85 | 0,5 | 0,8 | 0,95 |
| 13 | 0,12 | 0,3 | 0,85 | 0,9 | 0,2 | 0,65 |
| 14 | 0,175 | 0,3 | 0,85 | 0,9 | 0,2 | 0,95 |
| 15 | 0,452 | 0,3 | 0,85 | 0,9 | 0,8 | 0,65 |
| 16 | 0,66 | 0,3 | 0,85 | 0,9 | 0,8 | 0,95 |
| 17 | 0,118 | 0,3 | 0,55 | 0,5 | 0,2 | 0,65 |
| 18 | 0,173 | 0,9 | 0,55 | 0,5 | 0,2 | 0,95 |
| 19 | 0,336 | 0,9 | 0,55 | 0,5 | 0,8 | 0,65 |
| 20 | 0,486 | 0,9 | 0,55 | 0,5 | 0,8 | 0,95 |
| 21 | 0,158 | 0,9 | 0,55 | 0,9 | 0,2 | 0,65 |
| 22 | 0,228 | 0,9 | 0,55 | 0,9 | 0,2 | 0,95 |
| 23 | 0,373 | 0,9 | 0,55 | 0,9 | 0,8 | 0,65 |
| 24 | 0,544 | 0,9 | 0,55 | 0,9 | 0,8 | 0,95 |
| 25 | 0,127 | 0,9 | 0,85 | 0,5 | 0,2 | 0,65 |
| 26 | 0,184 | 0,9 | 0,85 | 0,5 | 0,2 | 0,95 |
| 27 | 0,457 | 0,9 | 0,85 | 0,5 | 0,8 | 0,65 |
| 28 | 0,67 | 0,9 | 0,85 | 0,5 | 0,8 | 0,95 |
| 29 | 0,137 | 0,9 | 0,85 | 0,9 | 0,2 | 0,65 |
| 30 | 0,201 | 0,9 | 0,85 | 0,9 | 0,2 | 0,95 |
| 31 | 0,471 | 0,9 | 0,85 | 0,9 | 0,8 | 0,65 |
| 32 | 0,689 | 0,9 | 0,85 | 0,9 | 0,8 | 0,95 |
Кроме вычисленных оценок коэффициентов регрессии функция "Регрессия" выдает также результаты регрессионного анализа (табл. 5.13): вычисленные значения откликов 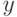 , разность между ними и измеренными в эксперименте в каждом наблюдении
, разность между ними и измеренными в эксперименте в каждом наблюдении  , среднеквадратические ошибки в определении коэффициентов регрессии
, среднеквадратические ошибки в определении коэффициентов регрессии 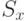 и откликов при определенных значениях факторов
и откликов при определенных значениях факторов 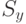 и некоторые другие.
и некоторые другие.
| Коэффициенты | Стандартная ошибка | t-статистика | |
|---|---|---|---|
 -пересечение -пересечение |
-0,52287 | 0,083821 | -6,23787 |
Переменная 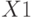
|
0,044568 | 0,034409 | 1,295248 |
Переменная 
|
0,270679 | 0,068279 | 3,964334 |
Переменная 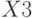
|
0,048634 | 0,051209 | 0,949722 |
Переменная 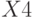
|
0,559089 | 0,034139 | 16,37673 |
Переменная 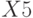
|
0,387762 | 0,068279 | 5,679123 |
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 1 | 0,027558 | 0,060442 | 1,141425 |
| 2 | 0,143886 | -0,01689 | -0,31889 |
| 3 | 0,363011 | -0,06001 | -1,13329 |
| 4 | 0,47934 | -0,03734 | -0,70515 |
| 5 | 0,047011 | 0,051989 | 0,981781 |
| 6 | 0,16334 | -0,01734 | -0,32746 |
| 7 | 0,382465 | -0,06547 | -1,23628 |
| 8 | 0,498794 | -0,03879 | -0,7326 |
| 9 | 0,108761 | 0,007239 | 0,136697 |
| 10 | 0,22509 | -0,05809 | -1,09701 |
| 11 | 0,444215 | 0,000785 | 0,014822 |
| 12 | 0,560544 | 0,092456 | 1,745995 |
| 13 | 0,128215 | -0,00822 | -0,15514 |
| 14 | 0,244544 | -0,06954 | -1,31331 |
| 15 | 0,463669 | -0,01167 | -0,22036 |
| 16 | 0,579998 | 0,080002 | 1,510813 |
| 17 | 0,027558 | 0,090442 | 1,707963 |
| 18 | 0,170627 | 0,002373 | 0,044804 |
| 19 | 0,389752 | -0,05375 | -1,01509 |
| 20 | 0,506081 | -0,02008 | -0,37922 |
| 21 | 0,073752 | 0,084248 | 1,590978 |
| 22 | 0,190081 | 0,037919 | 0,716081 |
| 23 | 0,409206 | -0,03621 | -0,68374 |
| 24 | 0,525535 | 0,018465 | 0,348706 |
| 25 | 0,135502 | -0,00850 | -0,16057 |
| 26 | 0,251831 | -0,06783 | -1,28096 |
| 27 | 0,470956 | -0,01396 | -0,26356 |
| 28 | 0,587285 | 0,082715 | 1,56204 |
| 29 | 0,154956 | -0,01796 | -0,33909 |
| 30 | 0,271285 | -0,07028 | -1,3273 |
| 31 | 0,490410 | -0,01941 | -0,36655 |
| 32 | 0,606739 | 0,082261 | 1,553472 |
Пример 5.10. На узел связи поступают заявки на передачу сообщений. Интервалы времени поступления заявок подчинены показательному закону с математическим ожиданием 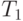 . На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени
. На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени ![[0\ldots T_{2}]](/sites/default/files/tex_cache/334386a39c69e0a015dc6cb9a0d70ebf.png) вероятности того, что каналы
вероятности того, что каналы  и
и 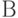 будут свободны, соответственно равны
будут свободны, соответственно равны 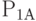 и
и 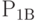 . При поступлении заявок после времени
. При поступлении заявок после времени 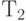 вероятности того, что каналы
вероятности того, что каналы  и
и 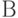 будут свободны, соответственно равны
будут свободны, соответственно равны  и
и 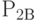 .
Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
.
Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
Построить имитационную модель "Обработка запросов на узле связи" с целью определения абсолютного и относительного числа потерянных заявок из их общего количества, поступивших на узел связи за время  ,
, 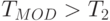 . Получить уравнение регрессии, связывающее относительную долю обслуженных заявок с интервалами их поступления и вероятностями
. Получить уравнение регрессии, связывающее относительную долю обслуженных заявок с интервалами их поступления и вероятностями 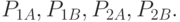
Решение
Имитационная модель построена в соответствии с алгоритмом (см. рис. 3.21). Для построения уравнения регрессии введем обозначения:
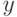 - отклик модели, вероятность ремонта СС с неисправными блоками
- отклик модели, вероятность ремонта СС с неисправными блоками  ,
,  и
и  ,
,  ,
, 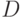 за время
за время  ;
;
 - фактор, представляющий вероятность
- фактор, представляющий вероятность 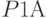 ;
;
 - фактор, представляющий вероятность
- фактор, представляющий вероятность 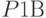 ;
;
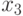 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
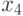 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
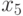 - фактор, представляющий интервалы поступления заявок
- фактор, представляющий интервалы поступления заявок  .
.
Исходные данные и результаты эксперимента приведены в табл. 5.14. Для регрессионного анализа также использовалась функция "Регрессия" MS Excel. Получено искомое уравнение:
| Номер отклика | 
|
|
|
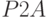
|
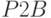
|

|
|---|---|---|---|---|---|---|
| 1 | 0,405 | 0,5 | 0,7 | 0,3 | 0,3 | 1 |
| 2 | 0,406 | 0,5 | 0,7 | 0,3 | 0,3 | 9 |
| 3 | 0,09 | 0,5 | 0,7 | 0,3 | 0,9 | 1 |
| 4 | 0,09 | 0,5 | 0,7 | 0,3 | 0,9 | 9 |
| 5 | 0,195 | 0,5 | 0,7 | 0,7 | 0,3 | 1 |
| 6 | 0,195 | 0,5 | 0,7 | 0,7 | 0,3 | 9 |
| 7 | 0,06 | 0,5 | 0,7 | 0,7 | 0,9 | 1 |
| 8 | 0,06 | 0,5 | 0,7 | 0,7 | 0,9 | 9 |
| 9 | 0,38 | 0,5 | 0,9 | 0,3 | 0,3 | 1 |
| 10 | 0,38 | 0,5 | 0,9 | 0,3 | 0,3 | 9 |
| 11 | 0,65 | 0,5 | 0,9 | 0,3 | 0,9 | 1 |
| 12 | 0,65 | 0,5 | 0,9 | 0,3 | 0,9 | 9 |
| 13 | 0,17 | 0,5 | 0,9 | 0,7 | 0,3 | 1 |
| 14 | 0,17 | 0,5 | 0,9 | 0,7 | 0,3 | 9 |
| 15 | 0,035 | 0,5 | 0,9 | 0,7 | 0,9 | 1 |
| 16 | 0,0348 | 0,5 | 0,9 | 0,7 | 0,9 | 9 |
| 17 | 0,375 | 0,9 | 0,7 | 0,3 | 0,3 | 1 |
| 18 | 0,376 | 0,9 | 0,7 | 0,3 | 0,3 | 9 |
| 19 | 0,06 | 0,9 | 0,7 | 0,3 | 0,9 | 1 |
| 20 | 0,06 | 0,9 | 0,7 | 0,3 | 0,9 | 9 |
| 21 | 0,165 | 0,9 | 0,7 | 0,7 | 0,3 | 1 |
| 22 | 0,165 | 0,9 | 0,7 | 0,7 | 0,3 | 9 |
| 23 | 0,03 | 0,9 | 0,7 | 0,7 | 0,9 | 1 |
| 24 | 0,0301 | 0,9 | 0,7 | 0,7 | 0,9 | 9 |
| 25 | 0,37 | 0,9 | 0,9 | 0,3 | 0,3 | 1 |
| 26 | 0,37 | 0,9 | 0,9 | 0,3 | 0,3 | 9 |
| 27 | 0,055 | 0,9 | 0,9 | 0,3 | 0,9 | 1 |
| 28 | 0,055 | 0,9 | 0,9 | 0,3 | 0,9 | 9 |
| 29 | 0,16 | 0,9 | 0,9 | 0,7 | 0,3 | 1 |
| 30 | 0,16 | 0,9 | 0,9 | 0,7 | 0,3 | 9 |
| 31 | 0,025 | 0,9 | 0,9 | 0,7 | 0,9 | 1 |
| 32 | 0,025 | 0,9 | 0,9 | 0,7 | 0,9 | 9 |
Результаты регрессионного анализа, аналогичные рассмотренным в примере 5.9 (табл. 5.13), приведены в табл. 5.15.
| Коэффициенты | Стандартная ошибка | t-статистика | |
|---|---|---|---|
 -пересечение -пересечение |
0,526135 | 0,211881 | 2,483165 |
Переменная 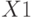
|
-0,23277 | 0,112257 | -2,0735 |
Переменная 
|
0,289906 | 0,224514 | 1,291259 |
Переменная 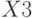
|
-0,48314 | 0,112257 | -4,30387 |
Переменная 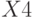
|
-0,25334 | 0,074838 | -3,38522 |
Переменная 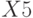
|
1,48E-05 | 0,005613 | 0,002645 |
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 1 | 0,391756 | 0,013244 | 0,113864 |
| 2 | 0,391875 | 0,014125 | 0,12144 |
| 3 | 0,23975 | -0,14975 | -1,28748 |
| 4 | 0,239869 | -0,14987 | -1,2885 |
| 5 | 0,1985 | -0,0035 | -0,03009 |
| 6 | 0,198619 | -0,00362 | -0,03111 |
| 7 | 0,046494 | 0,013506 | 0,116121 |
| 8 | 0,046613 | 0,013387 | 0,1151 |
| 9 | 0,449738 | -0,06974 | -0,59957 |
| 10 | 0,449856 | -0,06986 | -0,60059 |
| 11 | 0,297731 | 0,352269 | 3,02865 |
| 12 | 0,29785 | 0,35215 | 3,027629 |
| 13 | 0,256481 | -0,08648 | -0,74353 |
| 14 | 0,2566 | -0,0866 | -0,74455 |
| 15 | 0,104475 | -0,06948 | -0,59732 |
| 16 | 0,104594 | -0,06979 | -0,60006 |
| 17 | 0,29865 | 0,07635 | 0,656423 |
| 18 | 0,298769 | 0,077231 | 0,664 |
| 19 | 0,146644 | -0,08664 | -0,74492 |
| 20 | 0,146763 | -0,08676 | -0,74595 |
| 21 | 0,105394 | 0,059606 | 0,512468 |
| 22 | 0,105513 | 0,059487 | 0,511447 |
| 23 | -0,04661 | 0,076612 | 0,65868 |
| 24 | -0,04649 | 0,076594 | 0,658519 |
| 25 | 0,356631 | 0,013369 | 0,114939 |
| 26 | 0,35675 | 0,01325 | 0,113918 |
| 27 | 0,204625 | -0,14963 | -1,28641 |
| 28 | 0,204744 | -0,14974 | -1,28743 |
| 29 | 0,163375 | -0,00338 | -0,02902 |
| 30 | 0,163494 | -0,00349 | -0,03004 |
| 31 | 0,011369 | 0,013631 | 0,117195 |
| 32 | 0,011488 | 0,013512 | 0,116174 |
Вопросы для самоконтроля
- Что понимают под характеристикой случайных величин и процессов?
- Что такое несмещенная оценка характеристики случайной величины? Состоятельная? Эффективная?
- Что характеризует гистограмма? Правило построения гистограммы.
- В чем состоит сущность дисперсионного анализа?
- Что такое ошибки первого рода и второго рода при оценке гипотез?
- Что такое F - распределение и почему оно является мерой сравнения дисперсий случайных величин?
- Для чего используется критерий Вилькоксона?
- В чем состоит методика выявления несущественных факторов?
- Назначение корреляционного анализа.
- Назначение регрессионного анализа.
- Представьте графически виды корреляции между двумя переменными.
- Составьте систему уравнений для определения коэффициентов регрессии модели вида:
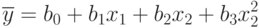
- Для линейной и нелинейной моделей, полученных в п. 5.12, вычислить и сравнить ошибки
 и
и 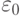 .
. - С объектом проведено
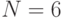 экспериментов. Данные экспериментов приведены в таблице:
экспериментов. Данные экспериментов приведены в таблице:
Построить линейную математическую модель функционирования объекта вида:
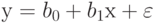 . Расчеты провести в таблице. Проверьте адекватность модели при абсолютной точности 0,2.
. Расчеты провести в таблице. Проверьте адекватность модели при абсолютной точности 0,2.