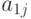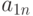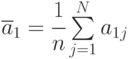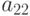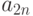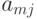|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
5.7. Однофакторный дисперсионный анализ
В современной жизни - военной и гражданской часто возникают проблемы, решение которых требует научного обоснования.
Однотипны ли патроны для конкретного образца стрелкового вооружения, выпускаемые на разных заводах?
Однородны ли, например, автоматы, выпускаемые на разных заводах?
Здесь в качестве исследуемого фактора выступают заводы. Разные, но однотипные по назначению - варианты фактора, которые можно трактовать как уровни факторов.
Аналогичная задача возникает при сравнении однотипных изделий, вырабатываемых с применением различных технологий. Здесь подлежит анализу фактор - технология производства.
Эти и подобные задачи являются задачами однофакторного дисперсионного анализа (ОДА).
Иногда возможны задачи одновременного исследования влияния двух и более факторов. Например, чем объяснить рассеивание попаданий в цель: конструкторскими особенностями стрелкового вооружения, выпущенного на разных заводах, или различиями в подготовке стрелков?
Исследованием влияния факторов и занимается факторный дисперсионный анализ.
Мы рассмотрим ОДА, наиболее актуальный анализ на практике. Теория рассматривает и многофакторный дисперсионный анализ. В нем процедуры подобны тем, которые мы рассмотрим в ОДА. Усложняются только расчеты и при необходимости, зная ОДА, овладеть методикой многофакторного дисперсионного анализа, не составит труда.
Эксперимент для выполнения ОДА состоит в накоплении результатов измерений контролируемого параметра (угла, расстояния, наработки на отказ некоторого изделия и т. д.) при каждом варианте исследуемого фактора.
Введем обозначения:
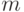 - число вариантов фактора;
- число вариантов фактора;
 - число измерений при каждом варианте;
- число измерений при каждом варианте;
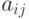 - результат каждого измерения;
- результат каждого измерения;
 - номер варианта фактора;
- номер варианта фактора;
 - номер измерения.
- номер измерения.
Схема эксперимента заключается в следующем.
Производится  измерений контролируемого параметра при
измерений контролируемого параметра при 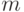 вариантах фактора.
вариантах фактора.
В принципе, число измерений может быть разным для каждого варианта фактора. Ход дальнейших рассуждений от этого не меняется.
Результаты эксперимента сводятся в таблицу (табл. 5.7).
Вопрос: влияют ли варианты фактора на точность измерений? Или, говоря языком математической статистики, являются результаты  измерений выборкой одной генеральной совокупности, или нет? Если да, то варианты фактора несущественны, если нет, то существенны.
измерений выборкой одной генеральной совокупности, или нет? Если да, то варианты фактора несущественны, если нет, то существенны.
Будем исходить из следующей нулевой гипотезы:
- наблюдения каждого варианта независимы;
- наблюдения каждого варианта имеют нормальное распределение;
- имеют одинаковую дисперсию
 ;
; - имеют одинаковые центры рассеивания.
Очевидно, если систематические ошибки вариантов не одинаковы, следует ожидать повышенного рассеивания выборочных средних  .
.
Для подтверждения или отрицания выдвинутой нулевой гипотезы об идентичности вариантов фактора проведем дисперсионный анализ.
Общее среднее арифметическое по всем  измерениям:
измерениям:

Сумма квадратов отклонений по всем  измерений, то есть по данным всего эксперимента:
измерений, то есть по данным всего эксперимента:
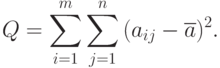
Эту сумму квадратов отклонений можно разложить на два независимых слагаемых:
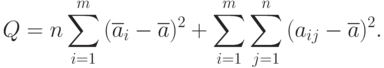
Обозначим:

Что такое 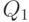 и
и 
 - сумма квадратов отклонений между вариантами фактора, так как
- сумма квадратов отклонений между вариантами фактора, так как  - среднее значение измеренного параметра
- среднее значение измеренного параметра 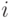 -го варианта фактора;
-го варианта фактора;
 - характеризует отклонения внутри каждого варианта.
- характеризует отклонения внутри каждого варианта.
Если принятая гипотеза о равенстве центров рассеивания 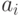 и дисперсий
и дисперсий 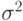 верна, тогда все
верна, тогда все  наблюдений значений
наблюдений значений  можно рассматривать как выборку из одной и той же нормальной совокупности с очевидной несмещенной оценкой дисперсии:
можно рассматривать как выборку из одной и той же нормальной совокупности с очевидной несмещенной оценкой дисперсии:

Можно показать, что величина
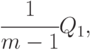
имеющая распределение 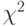 со степенями свободы
со степенями свободы 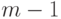 , является оценкой дисперсии
, является оценкой дисперсии 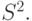
И величина

имеющая распределение 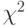 со степенями свободы
со степенями свободы  , также является оценкой дисперсии
, также является оценкой дисперсии  .
.
Из сказанного следует, что критерий

при нашей гипотезе и независимости  и
и 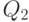 (это можно доказать) имеет F -распределение с
(это можно доказать) имеет F -распределение с  и
и  степенями свободы.
степенями свободы.
А дальше мы уже знаем, как поступить:
- выбираем уровень значимости
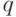 ;
; - вычисляем число
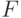 ;
; - из таблицы по величине
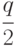 находим
находим  .
.
Если окажется

то есть мы попали в область маловероятных значений  , то выдвинутая гипотеза не подтверждается.А это значит, что варианты фактора не однотипны. Но если
, то выдвинутая гипотеза не подтверждается.А это значит, что варианты фактора не однотипны. Но если

то гипотеза об однородности вариантов фактора подтверждается, конечно, в рамках допустимого риска.
Пример 5.5. Необходимо проверить однотипность патронов к автомату Калашникова, изготовленных на трех заводах.
Для получения необходимых для дисперсионного анализа данных автомат закрепили в специальном станке и сделали из него по 50 выстрелов патронами каждого завода. По результатам стрельбы измерялись радиальные отклонения пробоин от точки прицеливания.
Результаты измерений приведены в табл. 5.8.
| Заводы | Эксперименты и отклонения, см | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | … | 26 | 27 | … | 49 | 50 | |
| № 1 | 3 | 2 | 1 | … | 4 | 3 | … | 1 | 3 |
| № 2 | 2 | 0 | 4 | … | 3 | 2 | … | 2 | 3 |
| № 3 | 2 | 3 | 3 | … | 1 | 0 | … | 1 | 5 |
Решение
Проверяем исходную гипотезу: патроны, выпускаемые на трех разных заводах, баллистически однотипны.
При выборе уровня значимости 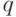 исходим из того, что более опасна ошибка второго рода - подтвердить ошибочный выбор. Примем
исходим из того, что более опасна ошибка второго рода - подтвердить ошибочный выбор. Примем  .
.
Число вариантов фактора: 
Число измерений:  .
.
При вычислениях опустим очевидные элементарные арифметические детали.
Средние отклонения пробоин при стрельбе патронами заводов № 1, № 2, № 3 равны соответственно:
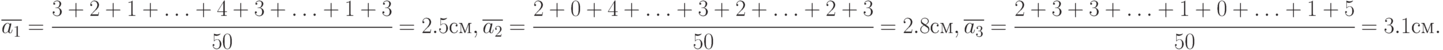
Среднее отклонение по 150 выстрелам:
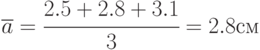
Средний квадрат расхождений между вариантами факторов:
![\cfrac{1}{m-1}Q_1=\cfrac{1}{m-1}n\sum\limits_{i=1}^{n}{(\overline{a_i}-\overline{a})^2}=\\
=\cfrac{50}{2}[(2.5-2.8)^2+(2.8-2.8)^2+(3.1-2.8)^2]=4,5 см^2](/sites/default/files/tex_cache/464c8c77ba3fa548e71115c5fbfa5102.png)
Число степеней свободы:  .
.
Средний квадрат расхождений внутри вариантов:
![\cfrac{1}{m(n-1)}Q_2=\cfrac{1}{m(n-1)} \sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}{(a_{ij}-\overline{a_i})^2} = \cfrac{1}{3.49}[(3-2.5)^2 + \\
+ (1-2.5)^2 + \ldots + (4-2.5)^2+ (3-2.5)^2 + \ldots + (1-2.5)^2 + (3-2.5)^2 + \\
+ (2-2.8)^2 + \ldots + (5-3.1)^2 ] = 2.2 см^2](/sites/default/files/tex_cache/9d63fe38d8dcb84deb918507a2eeab77.png)
Число степеней свободы:

Расчет F -критерия:

По табл. П.2 при 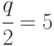 верхних пределов уклонения величины
верхних пределов уклонения величины 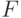 и имеющихся степенях свободы 2 и 147 находим
и имеющихся степенях свободы 2 и 147 находим 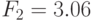 . Величина
. Величина 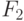 определена при
определена при  , так как табличные значения при
, так как табличные значения при  не определены. Нетрудно убедиться, что такое приближение вполне допустимо.
не определены. Нетрудно убедиться, что такое приближение вполне допустимо.
Поскольку  , делаем вывод о том, что выдвинутая гипотеза об однотипности партий патронов, выпускаемых тремя разными заводами, не опровергается (в пределах принятого уровня значимости).
, делаем вывод о том, что выдвинутая гипотеза об однотипности партий патронов, выпускаемых тремя разными заводами, не опровергается (в пределах принятого уровня значимости).