|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
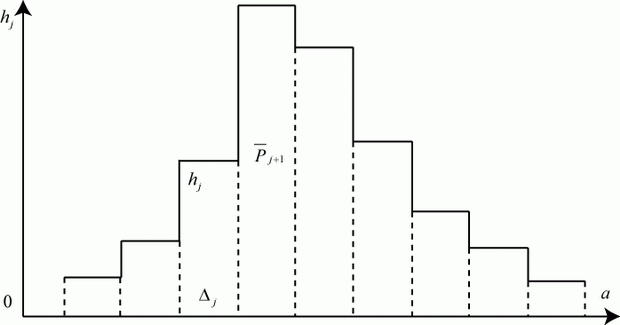
5.4. Гистограмма
Одной из задач моделирования может быть определение закона распределения вероятностей исследуемой случайной величины и количественных значений его характеристик.
Аналогом, моделью плотности распределения вероятности случайной величины является гистограмма, которую можно построить (аналитически или графически) по данным имитационного моделирования.
Гистограмма (рис. 5.1) строится так.
В результате  реализаций модели получен ряд случайных значений исследуемого параметра
реализаций модели получен ряд случайных значений исследуемого параметра  :
:  . Весь диапазон значений
. Весь диапазон значений  разбивается на
разбивается на  интервалов (разрядов). Числовой диапазон каждого интервала обозначим
интервалов (разрядов). Числовой диапазон каждого интервала обозначим  ,
, 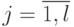 . Обычно все числовые диапазоны одинаковые:
. Обычно все числовые диапазоны одинаковые:  .
.
Для каждого интервала подсчитываем число значений 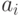 , попавших в него -
, попавших в него - 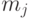 .
.
На каждом интервале строят прямоугольник с высотой  :
:

Площадь каждого прямоугольника гистограммы равна относительной частоте 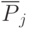 :
:
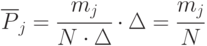
По выбору числа интервалов 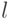 существуют разные эмпирические рекомендации, например:
существуют разные эмпирические рекомендации, например:

Чем больше  и
и  , а меньше
, а меньше  , тем ближе гистограмма совпадает с некоторым теоретическим распределением. Доказал это Валерий Иванович Гливенко - известный отечественный математик.
, тем ближе гистограмма совпадает с некоторым теоретическим распределением. Доказал это Валерий Иванович Гливенко - известный отечественный математик.
На основе очертания гистограммы делается предположение (выдвигается гипотеза) о совпадении полученного эмпирического распределения вероятностей с тем или иным теоретическим - нормальным, экспоненциальным, Вейбулла и т. д. Затем выполняется проверка этой гипотезы с помощью критериев согласия.В курсе высшей математики рассматриваются некоторые (критерий Колмогорова, критерий Смирнова и др.), наиболее популярными считают критерий хи-квадрат - критерий Пирсона, предложенный в 1903 г.
Оценки матожидания и дисперсии можно получить по данным гистограммы:
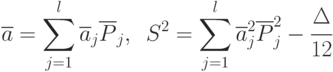
где 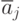 - среднее значение каждого интервала;
- среднее значение каждого интервала;
 - оценка по каждому интервалу;
- оценка по каждому интервалу;
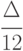 - поправка Шеппарда.
- поправка Шеппарда.
5.4. Элементы дисперсионного анализа. Критерий Фишера
Приведем понятия, которые используем в дальнейшем. В математической статистике (а это основной математический аппарат обработки результатов моделирования) широко используется понятие гипотезы.
Гипотезой называется предположение о:
- законах распределения вероятностей случайных величин;
- значениях характеристик случайных величин;
- совпадении законов распределения двух и более случайных величин и др.
Обычно исходную гипотезу называют нулевой и обозначают 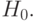 Противоположное утверждение называют конкурирующей гипотезой и обозначают
Противоположное утверждение называют конкурирующей гипотезой и обозначают 
Гипотеза подвергается проверке. Смысл этой проверки в том, чтобы принять или отклонить ее с допустимым минимальным риском. При этом возможны ошибки:
- забраковать проверяемую гипотезу, если она верна, что соответствует так называемой ошибке первого рода ;
- принять проверяемую гипотезу, когда она не верна,значит совершить ошибку второго рода.
Правило, которому принимается суждение об истинности или ложности основной гипотезы 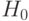 называют критерием проверки или критерием согласия.
называют критерием проверки или критерием согласия.
В практике моделирования и обработки экспериментальных данных очень часто необходимо решать проблему подтверждения или опровержения гипотезы о принадлежности двух или более выборок одной генеральной совокупности.
К такой проблеме приводят такие задачи:
- сравнительная оценка различных технологических процессов по их производительности, точности, экономичности;
- сравнение конструктивных особенностей приборов, машин, средств вооружения и др.
Признаки, по которым проводится сравнительная оценка, часто не являются детерминированными, обладают рассеиванием. Например, точность никогда не может быть абсолютной, так как измерительные приборы всегда несут в себе ошибку.
Наиболее общим и часто применяемым на практике методом сравнения качеств объектов является дисперсионный анализ.
Сущность дисперсионного анализа состоит в проверке гипотезы о тождественности выборочных дисперсий одной и той же генеральной дисперсии.
Почему исследователей интересует сравнение именно дисперсий, а не каких-либо других характеристик? Заметим, что есть методики сравнения, например, матожиданий и др., но они не обладают такой общностью, как дисперсионный анализ.
А дело в том, что дисперсия характеризует важные конструкторские и технологические показатели как:
- точность приборов;
- рассеивание точек попадания при стрельбе и др.
И еще дисперсионный анализ одновременно решает проблему проверки гипотезы о равенстве средних значений выборок.
Задача сравнения дисперсий сводится к проверке исходной гипотезы (нулевой гипотезы 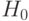 ) о принадлежности двух выборок
) о принадлежности двух выборок
одной и той же генеральной совокупности.
Для проверки гипотезы о равенстве дисперсий нужно иметь независимую функцию, вычислимую по данным эксперимента.
Такой функцией является функция Фишера (распределение Фишера, F -распределение), определяемая так:
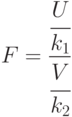
где  и
и 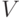 случайные величины, имеющие распределение
случайные величины, имеющие распределение 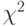 ;
;
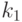 и
и 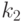 соответствующие степени свободы случайных величин
соответствующие степени свободы случайных величин  и
и 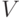 соответственно,
соответственно, 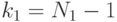 ,
, 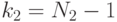 ;
;
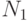 и
и  - количество испытаний (объемы выборок).
- количество испытаний (объемы выборок).
Почему 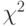 является мерой сравнения дисперсий? А потому, что дисперсии, являясь суммой квадратов ошибок, имеют распределение
является мерой сравнения дисперсий? А потому, что дисперсии, являясь суммой квадратов ошибок, имеют распределение 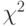 .
.
Распределение хи-квадрат определяется следующим образом:
![f(x)=\{ 1/[2^{\nu/2}\cdot\Gamma(\nu/2)] \}\cdot [x^{(\nu/2)-1}*e^{-x/2}],\,\,\nu=1,2,\ldots,\,\, 0< x](/sites/default/files/tex_cache/94b11ab2ea4085e161ad09fcc0d6197f.png)
где  - число степеней свободы,
- число степеней свободы,  - число Эйлера (2,71…),
- число Эйлера (2,71…),  - гамма-функция.
- гамма-функция.
График плотности F -распределения показан на рис. 5.2.
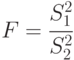
где 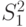 и
и 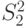 - несмещенные оценки дисперсий, полученных из независимых выборок, взятых из нормальных совокупностей, имеет распределение Фишера ( F -распределение).
- несмещенные оценки дисперсий, полученных из независимых выборок, взятых из нормальных совокупностей, имеет распределение Фишера ( F -распределение).
Величина F - случайна, поэтому судить однозначно по ее величине о подтверждении или опровержении гипотезы об однородности исследуемых выборок нельзя.
Поэтому вводится 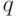 уровень значимости, численно равный вероятности неприемлемых отклонений от принятой гипотезы. Области неприемлемых значений
уровень значимости, численно равный вероятности неприемлемых отклонений от принятой гипотезы. Области неприемлемых значений 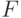 показаны на рис. 5.2 штриховкой. Граничные точки допустимых значений
показаны на рис. 5.2 штриховкой. Граничные точки допустимых значений 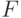 определяются точками
определяются точками 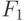 и
и  , соответствующих вероятностям
, соответствующих вероятностям  .
.
Если вычисленное по данным эксперимента значение 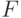 попадает в область между точками
попадает в область между точками 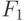 и
и  :
:
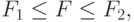
то принятая гипотеза не опровергается.
Заметим, что случайная величина
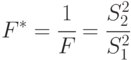
также имеет F -распределение со степенями свободы  и
и 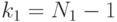 соответственно. Следовательно, вероятность попадания числа
соответственно. Следовательно, вероятность попадания числа 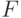 в левую критическую область равна:
в левую критическую область равна:
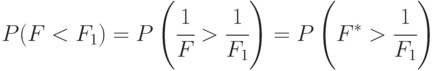
Отсюда следует, что левая критическая точка F -распределения соответствует правой критической точке 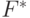 -распределения. Т. е. правые точки распределений
-распределения. Т. е. правые точки распределений 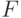 и
и 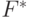 определяют левую и правую точки
определяют левую и правую точки 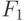 и
и  . Поэтому в таблицах представлены только правые
. Поэтому в таблицах представлены только правые 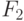 критические точки F -распределения.
критические точки F -распределения.
В таблицах значения 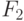 приведены в зависимости от
приведены в зависимости от  , числа степеней свободы
, числа степеней свободы 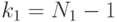 и
и  .
.
Обычно при вычислении 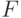 в числитель отношения
в числитель отношения  ставят значение большей дисперсии.
ставят значение большей дисперсии.
Итак, при  принятая гипотеза не опровергается, при
принятая гипотеза не опровергается, при 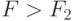 - не подтверждается.
- не подтверждается.
Пример 5.3. В часть поступили две буссоли. Первая из них при измерении пять раз одного и того же угла показала дисперсию  . По результатам семи измерений второй буссолью того же угла получена дисперсия
. По результатам семи измерений второй буссолью того же угла получена дисперсия 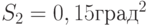 .
.
Однотипны ли буссоли? Одинаковы ли они по точности измерения углов? Выдвинем и проверим гипотезу об их однотипности для уровня значимости 
Решение
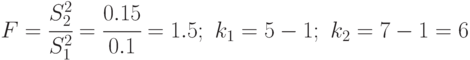
По таблицу F -распределения для степеней свобод 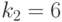 , соответствующей большей дисперсии, и
, соответствующей большей дисперсии, и  , соответствующей меньшей дисперсии, и уровню значимости
, соответствующей меньшей дисперсии, и уровню значимости  , находим
, находим  .
.
Так как 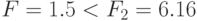 , то для уровня значимости
, то для уровня значимости  гипотеза об одинаковости буссолей не опровергается.
гипотеза об одинаковости буссолей не опровергается.
Итак: чем меньше уровень значимости 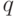 , тем меньше вероятность забраковать проверяемую гипотезу, когда она верна, т. е. совершить ошибку первого рода.
, тем меньше вероятность забраковать проверяемую гипотезу, когда она верна, т. е. совершить ошибку первого рода.
Но с уменьшением уровня значимости (увеличения  ) расширяется область допустимых ошибок, что приводит к увеличению вероятности принятия неверного решения,т. е. совершения ошибки второго рода.
) расширяется область допустимых ошибок, что приводит к увеличению вероятности принятия неверного решения,т. е. совершения ошибки второго рода.
В заключение изложенного отметим, что как бы ни был велик объем статистического материала 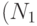 и
и  критерий Фишера (впрочем, как и любой другой) не может дать абсолютно достоверный ответ о справедливости или несправедливости проверяемой гипотезы, так как мы оперируем случайными числами.
критерий Фишера (впрочем, как и любой другой) не может дать абсолютно достоверный ответ о справедливости или несправедливости проверяемой гипотезы, так как мы оперируем случайными числами.
То есть, опровержение гипотезы ни в коем случае не означает категорического, логического опровержения гипотезы при 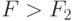 , равно как и подтверждение гипотезы при
, равно как и подтверждение гипотезы при  не означает категорического доказательства ее справедливости. Не исключено, что в том и в другом случае решение может оказаться ошибочным.
не означает категорического доказательства ее справедливости. Не исключено, что в том и в другом случае решение может оказаться ошибочным.
Суждение о подтверждении или отклонении выдвинутой гипотезы высказывается с определенной степенью достоверности.
Среди инженеров бытует шутливое изречение: статистика, как фонарный столб на улице: света дает мало, но при случае на него можно опереться.
Но свет-то дает! И другой альтернативы нет.