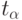|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
5.6. Критерий Вилькоксона
Как и в предыдущем случае решается следующая задача. Имеются две серии независимых наблюдений однородных случайных величин  и
и  , причем значения
, причем значения 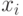 и
и  дают различные значения средних
дают различные значения средних 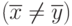 или (и) различные рассеивания. Возникает вопрос: можно ли считать эти расхождения существенными или расхождения зависят от случайных выборок?
или (и) различные рассеивания. Возникает вопрос: можно ли считать эти расхождения существенными или расхождения зависят от случайных выборок?
Простой в употреблении и вполне приемлемый по точности критерий для проверки гипотезы о тождественности функций распределения  и
и 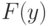 предложил в середине прошлого века Вилькоксон. Критерий назван его именем.
предложил в середине прошлого века Вилькоксон. Критерий назван его именем.
Рассматривается нулевая гипотеза:  . Конкурирующая гипотеза:
. Конкурирующая гипотеза: 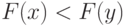 .
.
Критерий основан на подсчете числа инверсий. Инверсии определяются так.
Измеренные значения 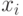 и
и  ,
, 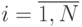 располагаются в общую последовательность в порядке возрастания их значений. Пусть это будет, например, так:
располагаются в общую последовательность в порядке возрастания их значений. Пусть это будет, например, так:
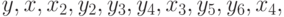
где 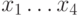 - члены, принадлежащие первой выборке;
- члены, принадлежащие первой выборке;
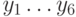 - члены второй выборки. Эта последовательность - не убывающая, содержащая
- члены второй выборки. Эта последовательность - не убывающая, содержащая  чисел,
чисел, 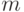 - количество чисел последовательности
- количество чисел последовательности  ,
,  - последовательности
- последовательности  .
.
Если гипотеза  верна, то достаточно очевидно, что числа из обеих последовательностей хорошо перемешиваются. Степень перемешивания определяется числом инверсий членов первой последовательности относительно второй. Если в упорядоченной общей последовательности некоторому
верна, то достаточно очевидно, что числа из обеих последовательностей хорошо перемешиваются. Степень перемешивания определяется числом инверсий членов первой последовательности относительно второй. Если в упорядоченной общей последовательности некоторому 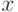 предшествует одно значение
предшествует одно значение  , это означает, что имеет место одна инверсия.
, это означает, что имеет место одна инверсия.
Если некоторому 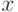 предшествуют
предшествуют  значений
значений  , то это значение
, то это значение 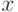 имеет
имеет  инверсий.
инверсий.
Для нашего примера член 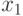 имеет одну инверсию с
имеет одну инверсию с 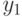 ; член
; член  - тоже одну с
- тоже одну с 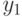 ; член
; член 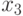 имеет четыре инверсии (с
имеет четыре инверсии (с 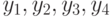 ); член
); член 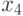 имеет шесть инверсий (с
имеет шесть инверсий (с 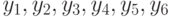 ).
).
Таким образом, общее число инверсий:
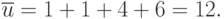
Показано, что случайная величина  уже при
уже при 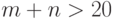 и
и 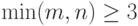 дает хорошее приближение к нормальному распределению с матожиданием и дисперсией:
дает хорошее приближение к нормальному распределению с матожиданием и дисперсией:
![M[u]=\cfrac{m-n}{2},\,\,\,
D[u]=\cfrac{m\cdot n}{12}(m+n+1),\,\,\,
\sigma_u=\sqrt{D[u]}](/sites/default/files/tex_cache/7bba2810a0f06eca88906ab954b49982.png)
При уровне значимости 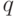 и нормальности распределения
и нормальности распределения  вероятность попадания значения
вероятность попадания значения  в критическую область (что означает не подтверждение нулевой гипотезы) равна:
в критическую область (что означает не подтверждение нулевой гипотезы) равна:
![P\{|M[u]-\overline{u}|>t_{\alpha}\sigma_u\}=q=1=2\Phi(t_{\alpha}),\\
P\{|M[u]-\overline{u}|>t_{\alpha}\sigma_u\ > \overline{u} > M[u]+t_{\alpha}\sigma_{u}}\}=q.](/sites/default/files/tex_cache/d730d30a7cf872ceae0ab3f9c1499714.png)
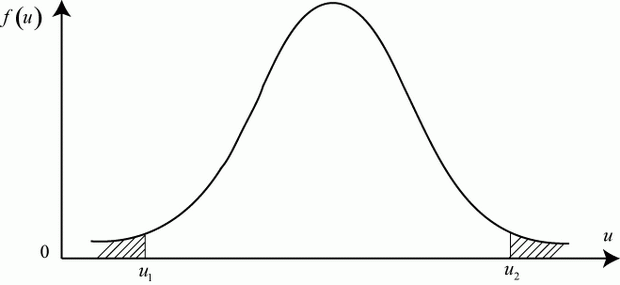
Отсюда следует, что левая критическая граница и правая критическая граница (рис. 5.3) равны соответственно:
![u_1=M[u]-t_{\alpha}\sigma_{u},\,\,\,u_2=M[u]+t_{\alpha}\sigma_{u}.](/sites/default/files/tex_cache/0b5623728c4800bac549e9d590b8b9fd.png)
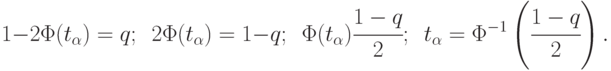
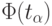 - функция Лапласа, с которой мы встречались ранее, она табулирована. Наиболее актуальные соответствия уровней значимости
- функция Лапласа, с которой мы встречались ранее, она табулирована. Наиболее актуальные соответствия уровней значимости  и аргументов функции Лапласа
и аргументов функции Лапласа 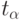 указаны в табл. 5.4
указаны в табл. 5.4
Пример 5.4. С целью проверки адекватности модели центра коммутации сообщений измерено время задержки передачи сообщений на модели центра и непосредственно на самом центре. Результаты измерений сведены в табл. 5.5.
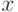 , сек , сек
|
0,8 | 1,9 | 3,0 | 3,5 | 3,8 | 2,5 | 1,7 | 0,9 | 1,0 | 2,3 |
|---|---|---|---|---|---|---|---|---|---|---|
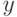 , сек , сек
|
1,4 | 2,1 | 3,1 | 3,6 | 2,7 | 1,8 | 1,1 | 0,2 | 1,6 | 2,8 |
Последовательность 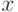 - отклики модели,
- отклики модели, 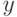 - данные, измеренные на центре. Проверка адекватности модели состоит в проверке нулевой гипотезы, то есть в том, что данные измерений идентичны в статистическом смысле. Решение
- данные, измеренные на центре. Проверка адекватности модели состоит в проверке нулевой гипотезы, то есть в том, что данные измерений идентичны в статистическом смысле. Решение
Составим в порядке возрастания общую последовательность времен задержек 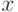 и
и 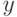 (табл. 5.6).
(табл. 5.6).
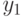
|

|

|
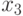
|
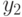
|
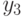
|

|
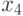
|
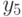
|
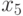
|
|---|---|---|---|---|---|---|---|---|---|
| 0,2 | 0,8 | 0,9 | 1,0 | 1,1 | 1,4 | 1,6 | 1,7 | 1,8 | 1,9 |
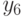
|

|

|
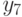
|
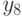
|
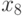
|
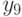
|
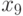
|
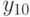
|
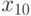
|
| 2,1 | 2,3 | 2,5 | 2,7 | 2,8 | 3,0 | 3,1 | 3,5 | 3,6 | 3,8 |
Расчет числа инверсий для  :
:
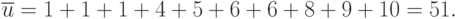
Расчет характеристик:
![M[u]=\cfrac{10\cdot 10}{2} = 50 c,\,\,\,
D[u]= \cfrac{10\cdot 10}{12}(10+10+1) =175 c^2,\\
\sigma_u=\sqrt{175}=13.23 c](/sites/default/files/tex_cache/7ac45d5230dfc22823e20d29d7e2ec6b.png)
Примем уровень значимости  . Тогда
. Тогда 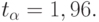
![u_{2} =M[u]+t_{\alpha }\sigma _{\alpha } =50 + 1.96?13.23\approx 74 .](/sites/default/files/tex_cache/8e24fe5c3d8761825bfaa13e45b66d60.png)
![u _{1} =M[u]-t_{\alpha }\sigma _{\alpha } =50-1.96\cdot 13.23 \approx 24.](/sites/default/files/tex_cache/5069e8a827e847fb2bc18fde3f18e68a.png)
Проверка гипотезы 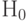 :
:

Гипотеза об идентичности распределений времен ожиданий в модели и в объекте не опровергается.
В заключение отметим, что при малых  и
и  (
( 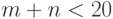 ) для критерия Вилькоксона составлены таблицы критических точек
) для критерия Вилькоксона составлены таблицы критических точек 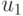 и
и 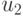 для различных уровней значимости
для различных уровней значимости 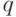 . Эти таблицы приводятся в широко известных изданиях, например, Б. Л. ван дер Варден "Математическая статистика", Б. В. Гнеденко и др. "Математические методы в теории надежности".
. Эти таблицы приводятся в широко известных изданиях, например, Б. Л. ван дер Варден "Математическая статистика", Б. В. Гнеденко и др. "Математические методы в теории надежности".