| Россия |
Алгоритмы: машины Тьюринга
Основные определения
Рассматриваемая в этом разделе модель алгоритмов была предложена английским математиком Тьюрингом в 1937 г. еще до создания современных компьютеров1Аналогичная модель вычислений была примерно в то же время определена Е. Постом. Поэтому иногда такие машины называют машинами Тьюринга-Поста Он исходил из общей идеи моделирования работы вычислителя, оперирующего в соответствии с некоторым строгим предписанием. В машине Тьюринга расчленение процесса вычисления на элементарные шаги доведено в известном смысле до предела. Элементарным действием является замена одного символа в ячейке на другой и перемещение к соседней ячейке. При таком подходе процесс вычисления значительно удлиняется, но зато логическая структура процесса сильно упрощается и приобретает удобный для теоретического исследования вид.
Машина Тьюринга (м.Т.) состоит из неограниченной в обе стороны ленты,
разбитой на ячейки, по которой передвигается головка машины.
Такая "бесконечность" ленты является математической абстракцией,
отражающей потенциальную неограниченность памяти вычислителя.
Разумеется, в каждом завершающемся вычислении используется только конечная часть
этой памяти - конечное число ячеек.
В каждой
ячейке ленты записан один символ из конечного внешнего алфавита машины 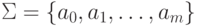 . Головка машины представляет конечный автомат,
который в каждый момент
времени находится в одном из внутренних состояний Q ={q0,q1,... ,
qn }. На каждом шаге головка в зависимости от своего
внутреннего состояния и символа в ячейке, которую она наблюдает,
изменяет свое внутреннее состояние и содержимое наблюдаемой ячейки
и может сдвинуться на одну ячейку вправо или влево либо остаться
на месте.
. Головка машины представляет конечный автомат,
который в каждый момент
времени находится в одном из внутренних состояний Q ={q0,q1,... ,
qn }. На каждом шаге головка в зависимости от своего
внутреннего состояния и символа в ячейке, которую она наблюдает,
изменяет свое внутреннее состояние и содержимое наблюдаемой ячейки
и может сдвинуться на одну ячейку вправо или влево либо остаться
на месте.
Дадим более формальное определение.
Определение 9.1. Машина Тьюринга - это система вида
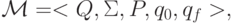
включающая следующие компоненты:
- Q ={q0,q1,... ,qn } - внутренний алфавит (алфавит состояний);
-
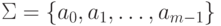 - внешний алфавит (алфавит ленты );
- внешний алфавит (алфавит ленты ); -
P - программа машины, в которой для каждой пары
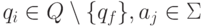 имеется (одна!) команда вида
имеется (одна!) команда вида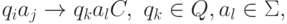
-
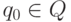 - начальное состояние;
- начальное состояние; -
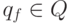 - заключительное состояние.
- заключительное состояние.
Выделим в алфавите  специальный пустой символ
специальный пустой символ 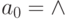 и будем считать, что во всех ячейках ленты, кроме конечного их числа, в начальный и во все последующие моменты находится пустой символ.
и будем считать, что во всех ячейках ленты, кроме конечного их числа, в начальный и во все последующие моменты находится пустой символ.
Будем говорить, что некоторый символ стирается, если он заменяется на пустой. Два слова из 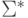 будем считать равными, если они совпадают после
отбрасывания всех пустых символов слева и справа. Например,
будем считать равными, если они совпадают после
отбрасывания всех пустых символов слева и справа. Например,  , но
, но  .
.
Как и для конечных автоматов, программу P можно задавать с помощью таблицы
размера n x m, строки которой соответствуют состояниям из Q,
а столбцы - символам из входного алфавита 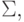 в которой на пересечении строки qi и столбца aj стоит тройка qk al C - правая часть команды qi aj -> qk al C.
в которой на пересечении строки qi и столбца aj стоит тройка qk al C - правая часть команды qi aj -> qk al C.
Определение 9.2. Назовем конфигурацией м.Т. 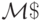 в некоторый момент времени слово K= wл qi aj wп, где
в некоторый момент времени слово K= wл qi aj wп, где 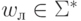 - слово на ленте левее текушего положения головки, qi - внутреннее состояние в данный момент, aj - символ, обозреваемый головкой,
- слово на ленте левее текушего положения головки, qi - внутреннее состояние в данный момент, aj - символ, обозреваемый головкой, 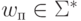 - слово на ленте правее текушего положения головки.
- слово на ленте правее текушего положения головки.
Будем считать, что слово wл aj wп содержит
все значащие символы на ленте. Поэтому, с точностью до
описанного выше равенства слов, конфигурация определена однозначно.
В частности, если 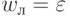 , т.е. пусто, то левее положения головки все ячейки пусты, а если
, т.е. пусто, то левее положения головки все ячейки пусты, а если  , то
правее положения головки все ячейки пусты.
, то
правее положения головки все ячейки пусты.
Начальная конфигурация - это конфигурация вида q0w, т.е. в начальный момент времени головка в состоянии q0 обозревает первый символ входного слова w. { it Заключительная } конфигурация - это конфигурация вида w1 qf w2, в которой машина находится в заключительном состоянии qf.
Определение 9.3. Скажем, что конфигурация K= w1 qi aj w2 м.Т. 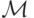 за один шаг (такт) переходит в конфигурацию
за один шаг (такт) переходит в конфигурацию 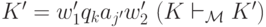 , если в программе имеется команда qi aj -> qk al C и при этом,
, если в программе имеется команда qi aj -> qk al C и при этом,
- если С=Н, то w1'=w1, w2'=w2 и a{j'}=al;
- если С=Л, то w1=w1' a, a{j'}=a, w2'=al w2 (если
 то
то  и
и 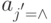 );
); - если С=П, то w2=aw2', a{j'}=a, w1'=w1 al (если
 то
то 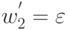 и
и 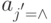 ).
).
Как обычно, через 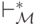 обозначим рефлексивное и транзитивное
замыкание отношения
обозначим рефлексивное и транзитивное
замыкание отношения 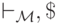 а
а 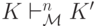 будет
означать, что конфигурация K за n шагов переходит в K'.
(Если из контекста ясно, о какой машине идет речь, то
индекс
будет
означать, что конфигурация K за n шагов переходит в K'.
(Если из контекста ясно, о какой машине идет речь, то
индекс 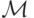 будем опускать).
будем опускать).
Пример 9.1.
Например, ситуации, представленной на рис.9.1 слева соответствует конфигурация 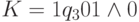 . Предположим, что программа P содержит команду q30 -> q51 П. Тогда после выполнения этой команды K перейдет за один шаг в конфигурацию
. Предположим, что программа P содержит команду q30 -> q51 П. Тогда после выполнения этой команды K перейдет за один шаг в конфигурацию 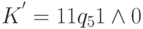 , показанную на этом рисунке
справа. Следовательно,
, показанную на этом рисунке
справа. Следовательно,  .
.
Определение 9.4. Вычисление м.Т.  на входе w - это конечная или
бесконечная последовательность конфигураций
на входе w - это конечная или
бесконечная последовательность конфигураций 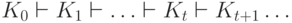 такая, что K0=q0w - начальная конфигурация.
Эта последовательность конечна, когда
ее последняя конфигурация Kn= v1 qf v2 - заключительная.
В этом случае вычисление назовем результативным, а слово v = v1 v2 -
его результатом на входе w (всегда будем предполагать, что v не
содержит пустых символов слева и справа).
такая, что K0=q0w - начальная конфигурация.
Эта последовательность конечна, когда
ее последняя конфигурация Kn= v1 qf v2 - заключительная.
В этом случае вычисление назовем результативным, а слово v = v1 v2 -
его результатом на входе w (всегда будем предполагать, что v не
содержит пустых символов слева и справа).
Определение 9.5. Скажем, что м.Т.  вычисляет частичную словарную функцию
вычисляет частичную словарную функцию 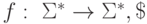 если для каждого слова w из области определения f существует результативное вычисление
если для каждого слова w из области определения f существует результативное вычисление 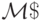 с результатом
с результатом 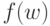 , а если f(w) не определена
, а если f(w) не определена 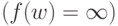 , то вычисление
, то вычисление  на входе w бесконечно.
на входе w бесконечно.
Скажем, что две м.Т.  и
и  эквивалентны, если они вычисляют одинаковые функции.
эквивалентны, если они вычисляют одинаковые функции.
Далее мы будем также рассматривать вычисления арифметических функций, т.е. функций с натуральными аргументами, принимающих натуральные значения. Для представления натуральных чисел используем унарное кодирование: число n будет представляться как слово из n палочек |n, а последовательные аргументы будем отделять *.
Определение 9.6. Скажем, что м.Т.  вычисляет частичную арифметическую функцию f: Nk -> N, если для любого набора чисел (x1,x2, ... ,xk), на котором f определена, существует
результативное вычисление
вычисляет частичную арифметическую функцию f: Nk -> N, если для любого набора чисел (x1,x2, ... ,xk), на котором f определена, существует
результативное вычисление  на входе
на входе  с результатом
с результатом 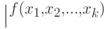 ,
а если
,
а если 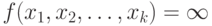 ,
то вычисление
,
то вычисление 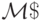 на соответствующем входе бесконечно.
на соответствующем входе бесконечно.
Аналогичное определение можно дать и для других спосбов кодирования чисел (двоичного, десятичного и др.). Ниже мы покажем, что класс вычислимых функций не зависит от выбора одного из таких кодирований.

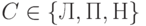 задает сдвиг
задает сдвиг