| Россия |
Алгоритмы: машины Тьюринга
Тьюрингово программирование
В этом разделе мы приведем примеры вычислений на машинах Тьюринга
и рассмотрим некоторые общие приемы, позволяющие комбинировать программы
различных м. Т. для получения более сложных вычислений. Будем считать, что
ячейки ленты м.Т. занумерованы от  до
до  , причем
в начальной конфигурации головка находится в 1-ой ячейке:
, причем
в начальной конфигурации головка находится в 1-ой ячейке:
- Ясно, что м.Т.
 проходит по массиву палочек слева направо и записывает в первой пустой ячейке новую |.
проходит по массиву палочек слева направо и записывает в первой пустой ячейке новую |. -
Бинарное кодирование.
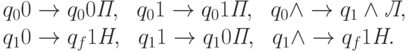
Нетрудно видеть, что эта машина в состоянии q0 находит младший разряд двоичного входа, затем в состоянии q1, идя справа налево, заменяет единицы на нули до тех пор, пока не находит 0 (или
 ) и заменяет его на 1. Следовательно, м.Т.
) и заменяет его на 1. Следовательно, м.Т. 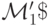 вычисляет функцию f(x) = x+1.
вычисляет функцию f(x) = x+1.
Рассмотрим функцию копирования (дублирования) слов в алфавите 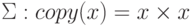 (мы предполагаем, что
(мы предполагаем, что 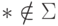 ).
).
Для ее реализации используем один из типичных приемов Тьюрингова программирования - { it расширение алфавита}.Пусть 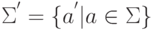 и
и 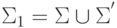 . М.Т.
. М.Т. 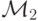 , копирующая вход, работает следующим образом:
, копирующая вход, работает следующим образом:
- отмечает 1-ый символ входа, идет направо, ставит * после входа и возвращается в начало:
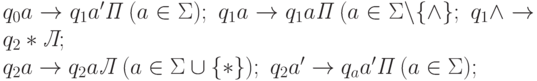
- в состоянии qa движется направо и записывает a в первую свободную ячейку:
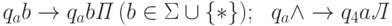
- возвращается в отмеченную ячейку и передвигает метку ' на одну ячейку вправо, снова переходя в состояние q2:
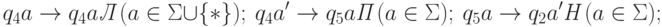
- увидев символ * в состоянии q5, останавливается:
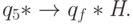
Из этого описания непосредственно следует, что 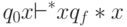 для любого
для любого 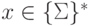 .
.

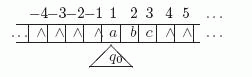
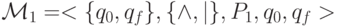 , где
, где 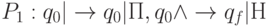 .
.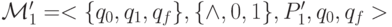 , где
, где 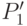 :
: