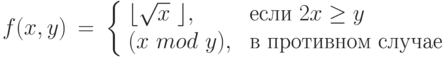| Россия, Москва, МГУПИ |
Алгоритмы: машины Тьюринга
Ветвление (условный оператор)
Машину Тьюринга  будем называть распознающей,
если для некоторого алфавита
будем называть распознающей,
если для некоторого алфавита  и каждого входа
и каждого входа 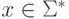 , на котором
, на котором  останавливается,
ее результат
останавливается,
ее результат  , т.е.
, т.е.  вычисляет
некоторую двузначную функцию (возможно частичную) на словах
из
вычисляет
некоторую двузначную функцию (возможно частичную) на словах
из 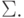
Лемма 9.5. Пусть  - распознающая м.Т., м.Т.
- распознающая м.Т., м.Т.  вычисляет функцию f(x),
а м.Т.
вычисляет функцию f(x),
а м.Т. 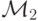 - функцию g(x). Тогда существует м.Т.
- функцию g(x). Тогда существует м.Т. 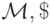 вычисляющая функцию
вычисляющая функцию
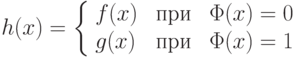
Доказательство. Требуемая м.Т. 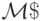 вначале копирует вход x и получает на ленте слово x*x, затем вычисляет параллельную композицию функций
вначале копирует вход x и получает на ленте слово x*x, затем вычисляет параллельную композицию функций 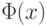 и тождественной функции e(x)=x и переходит в конфигурацию
и тождественной функции e(x)=x и переходит в конфигурацию 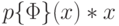 . Выбор между f и g происходит
по следующим командам:
. Выбор между f и g происходит
по следующим командам:
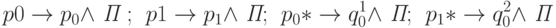
Кроме того, обеспечим переход в новое заключительное состояние:
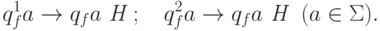
Таким образом, мы реализовали в терминах машин Тьюринга обычный в языках программирования оператор ветвления:
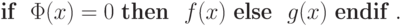
Повторение (цикл)
Используя конструкцию для ветвления легко реализовать в терминах машин Тьюринга и оператор цикла.
Лемма 9.6. Пусть  - распознающая м.Т., а м.Т.
- распознающая м.Т., а м.Т.  вычисляет функцию f(x).
Тогда существует м.Т.
вычисляет функцию f(x).
Тогда существует м.Т. 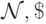 которая вычисляет функцию, задаваемую выражением:
которая вычисляет функцию, задаваемую выражением:
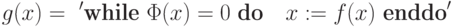
Доказательство. Действительно, пусть м.Т. 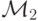 - вычисляет тождественную функцию g(x)=x. Построим по м.Т.
- вычисляет тождественную функцию g(x)=x. Построим по м.Т. 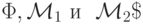 м.Т.
м.Т. 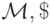 реализующую ветвление как в лемме 9.5. Тогда
искомая м.Т.
реализующую ветвление как в лемме 9.5. Тогда
искомая м.Т. 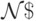 получается из
получается из 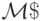 заменой команд
заменой команд 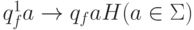 на
соответствующие команды
на
соответствующие команды  ,
обеспечивающие зацикливание.
,
обеспечивающие зацикливание.
Реализованные выше операции над машинами Тьюринга
и вычислимыми функциями позволяют получать программы новых м.Т., используя обычные конструкции языка программирования
"высокого" уровня: последовательную и параллельную композицию, ветвление и цикл. Пусть 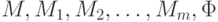 - машины Тьюринга. Последовательную композицию M1 и M2 будем обозначать M1;M2, параллельную композицию M1, M2,... , Mm
обозначаем как
- машины Тьюринга. Последовательную композицию M1 и M2 будем обозначать M1;M2, параллельную композицию M1, M2,... , Mm
обозначаем как 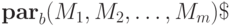 (здесь b -
это символ, разделяющий аргументы и результаты этих машин), ветвление -
(здесь b -
это символ, разделяющий аргументы и результаты этих машин), ветвление -

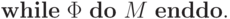
Пример 9.4. Рассмотрим в качестве примера задачу
перевода чисел из унарной системы счисления в двоичную.
Пусть fub(|n) = n(2) для всех 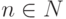 , где n(2) - двоичная запись числа n.
, где n(2) - двоичная запись числа n.
Пусть M1 - м.Т., которая начальную конфигурацию q0 ,|n переводит в конфигурацию q1 ,0*|n; M2 - м.Т., которая прибавляет 1 к двоичному
числу-аргументу (см. пример ref{ex8-suc}); M3 - м.Т., которая вычитает 1 из унарного
числа;  - м.Т., которая на аргументе вида x*|y выдает
0, если число y > 0, и выдает 1 при y=0 (т.е. на аргументе
- м.Т., которая на аргументе вида x*|y выдает
0, если число y > 0, и выдает 1 при y=0 (т.е. на аргументе  ); M4 - м.Т., которая стирает * в аргументе вида x* и
останавливается. Реализация каждой из указанных м.Т. очевидна.
Теперь требуемая м.Т. Mub, вычисляющая fub, получается как
); M4 - м.Т., которая стирает * в аргументе вида x* и
останавливается. Реализация каждой из указанных м.Т. очевидна.
Теперь требуемая м.Т. Mub, вычисляющая fub, получается как
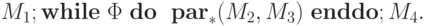
Действительно, после работы M1 получаем конфигурацию q10*|n. Предположим теперь по индукции, что после i (i <n) итераций цикла
while получается конфигурация q1 i(2)*|n-i.
Тогда на (i+1) -ой итерации цикла после параллельного
применения M2 к i(2) и M3 к |n-i
получаем конфигурацию q1(i+1)(2)*|n-i-1.
Поэтому после n итераций получится конфигурация 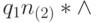 . На ней
. На ней  выдаст 1, и цикл завершится с записью
выдаст 1, и цикл завершится с записью 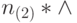 на ленте,
из которой M4 сотрет * и оставит требуемый результат n(2).
на ленте,
из которой M4 сотрет * и оставит требуемый результат n(2).
Отметим, что из приведенного примера и из задачи \oldref{prb3-6}(a) следует, что класс вычислимых на м.Т. арифметических функций не зависит от выбора унарного или двоичного кодирования аргументов и результатов. Это же справедливо и для троичной, десятичной и других позиционных систем счисления ( почему ?).
Задачи
Задача 9.1. Постройте м.Т. для функции копирования, не
увеличивая исходный алфавит 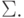
Задача 9.2. Постройте программу м.Т., которая выполняла бы
перенос непустого слова в заданное место ленты, т.е. для любого
слова  и n > 0 выполняла
преобразование конфигураций:
и n > 0 выполняла
преобразование конфигураций: 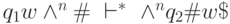 .
.
Задача 9.3. Достройте программу м.Т. 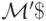 из леммы 9.1 на этапах 3 и 4.
из леммы 9.1 на этапах 3 и 4.
Задача 9.4. Докажите, что односторонняя м.Т.  построенная в лемме 9.2, корректно моделирует исходную м.Т.
построенная в лемме 9.2, корректно моделирует исходную м.Т. 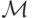 .
.
Задача 9.5. Другой, по сравнению с конструкцией леммы 9.2,
подход к моделированию двухсторонней ленты на
односторонней заключается в том, чтобы содержимое правой полуленты  хранить в четных ячейках
хранить в четных ячейках 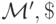 а содержимое
левой полуленты - в нечетных, поместив в 1-ю ячейку специальный маркер.
Постройте программу, реализующую этот подход (ее достоинство -
увеличение алфавита ленты всего на 1 символ).
а содержимое
левой полуленты - в нечетных, поместив в 1-ю ячейку специальный маркер.
Постройте программу, реализующую этот подход (ее достоинство -
увеличение алфавита ленты всего на 1 символ).
Задача 9.6. Достройте программу м.Т. 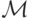 из
леммы 9.4 на этапах 1, 3 и 5.
из
леммы 9.4 на этапах 1, 3 и 5.
Задача 9.7. Построить программы машин Тьюринга, вычисляющих следующие функции.
- Перевод из двоичной системы в унарную: fbu(n(2))= |n.
- Сложение и вычитание в двоичной системе: sum(n*m)=n+m и
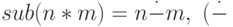 совпадает с - при n >= m и
совпадает с - при n >= m и 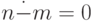 при m > n ).
при m > n ). - Умножение в двоичной системе: mul(n*m)= n x m. ( Реализуйте алгоритм умножения "в столбик".)
- Возведение в степень: exp(n*m)= nm.
- Извлечение квадратного корня:
 .
. - Логарифмирование:
 .
. - Деление:
 .
. - Остаток от деления: rest(n*m) = n mod m.
- Функция выбора аргумента:
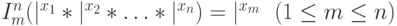 .
.
Задача 9.8. Используя машины Тьюринга из предыдущей задачи, построить программы машин Тьюринга, вычисляющих следующие функции.
Задача 9.9. Докажите, что всякую арифметическую функцию f(x),
вычислимую на некоторой м. Т. 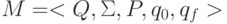 , можно также вычислить на м. Т. M',, алфавит ленты которой содержит лишь два символа
, можно также вычислить на м. Т. M',, алфавит ленты которой содержит лишь два символа  и |. (Указание: используйте для моделирования
одного символа из
и |. (Указание: используйте для моделирования
одного символа из  блок из нескольких подряд идущих ячеек,
содержащих его код в алфавите
блок из нескольких подряд идущих ячеек,
содержащих его код в алфавите 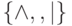 ) и замените
каждую команду M группой команд, обрабатывающих соответствующий
блок ячеек).
) и замените
каждую команду M группой команд, обрабатывающих соответствующий
блок ячеек).
Задача 9.10. Построить машину Тьюринга, определяющую по слову x в алфавите {1, 2} симметрично ли оно, т. е. вычисляющую функцию:
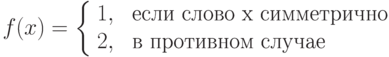
Задача 9.11.
Построить машину Тьюринга, сравнивающую два слова x=x1x2... xn и y=y1y2... ym в алфавите {1, 2, 3} лексикографически: ![x \prec y \Leftrightarrow\ \exists i \leq n [(x_1=y_1)\ \&\ ( x_2=y_2)\ \& \ldots\ (x_{i-1}=y_{i-1})
\ \&\ ( x_i < y_i )]](/sites/default/files/tex_cache/906eaf76ce1a1acb04eb948e9f81cef0.png) или для некоторого непустого слова x' выполнено y = x x'.
Эта машина Тьюринга должна вычислять функцию:
или для некоторого непустого слова x' выполнено y = x x'.
Эта машина Тьюринга должна вычислять функцию: