SPMD-технология на базе симметричной ВС
Программирование
Здесь приведены примеры экспериментального программирования некоторых задач. Сложился общий подход, который заключается в выделении в каждой задаче опорного массива, распределяемого для обработки разными процессорными элементами. Все другие структурированные данные "привязываются" к элементам опорного массива. Опыт программирования показывает, что такая практическая возможность существует всегда. Опорный массив может быть любой размерности и структуры. В различных задачах это — массив, подвергающийся операции "свертки", сведенный к одномерному (линейному) массиву элементов матрицы, записей в списке, формируемых логических цепочек в задаче логического вывода, фреймов базы знаний и др. Представляется логичным распределение нейронов для обработки нейросети. Т.е. нейроны должны составлять опорный массив. Легко просматривается план обработки нейросети как в режиме обучения (например, при реализации метода "обратного прохождения ошибки"), так и в режиме распознавания. Экспериментальное программирование логического вывода на языке ПРОЛОГ наводит на обобщение. А именно, принцип параллельного ветвления возможных вариантов преобразования сложной цепи полностью соответствует реализации метода "ветвей и границ". И здесь целесообразно применение счетчиков для развития возможных вариантов ветвления. Это определяет возможность параллельного решения сложных задач оптимизации, основанного на переборе с возвратом и имеющего экспоненциальную сложность.
Векторная операция свертки
Под операцией свертки понимается преобразование вектора в скаляр. Такой операции может соответствовать сложение или умножение всех элементов массива, нахождение максимума или минимума и др. Небольшая модификация этой операции позволяет получить скалярное произведение, произвести численное интегрирование.
Найдем способом "пирамиды" произведение элементов массива 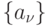 ,
,  .
Пусть для наглядности N = 4. Для k = 10 схема счета приведена
на рис. 12.2. Введены вершины a10,...,a17, соответствующие
промежуточным результатам, и вершина a18, соответствующая результату счета.
У каждой вершины, обозначающей операцию, указан номер выполняющего ее процессора.
Это закрепление операций за процессорами в программе жестко не
планируется, так как программа не зависит ни от числа процессоров, ни от
числа элементов в массиве. Однако при организации программы порядок
использования процессоров предусматривается и для известного их числа
может быть предсказан.
.
Пусть для наглядности N = 4. Для k = 10 схема счета приведена
на рис. 12.2. Введены вершины a10,...,a17, соответствующие
промежуточным результатам, и вершина a18, соответствующая результату счета.
У каждой вершины, обозначающей операцию, указан номер выполняющего ее процессора.
Это закрепление операций за процессорами в программе жестко не
планируется, так как программа не зависит ни от числа процессоров, ни от
числа элементов в массиве. Однако при организации программы порядок
использования процессоров предусматривается и для известного их числа
может быть предсказан.
Пусть дескрипторы массивов, комплектом которых располагает каждый процессор в своей памяти, содержат дескрипторные элементы, облегчающие аппаратную (микропрограммную) реализацию нахождения и анализа адресов элементов массива. Каждый дескрипторный элемент выполняет определенную функцию; при отсутствии необходимости некоторые дескрипторные элементы могут не формироваться. Как дескриптор в целом, так и каждый его элемент адресуемы и располагаются в смежных регистрах.
Сформируем в ПП i, i = 0,...,N-1, дескриптор D1 массива {a0, a2, a4,...,a2k-4},
содержащий восемь (максимальное количество) дескрипторных
элементов, D1 = {D10,...,D17}. В D10
содержится адрес a0 первого элемента
массива, D11 содержит шаг h = 2 переадресации
(предполагаем, что элементы
массива 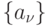 в памяти расположены в смежных ячейках), D12 — количество k-1 элементов, D13 — адрес последнего
( a2k-4 ) элемента массива. Элемент D14 служит для организации автоматической переадресации при
последовательном обращении к данному массиву. В D14 хранится адрес a0+jh для выборки
элемента массива при j -м ( j = 0,1,...) обращении к
нему ( j может быть
параметром цикла). После выполнения обращения этот адрес увеличивается на
шаг h, т.е. выполняется операция (D14) :=
(D14)+(D11). Следующая группа
дескрипторных элементов предназначена для автоматического распределения
элементов массива между процессорами. В D15 содержится адрес a0+ih, где i — номер процессора. Таким образом, каждый процессор
формирует собственное
значение D15, располагая адресом регистра в своей памяти,
содержащего значение i, для начального обращения к "своему"
элементу массива. В D16 содержится значение Nh, используемое для
переадресации к следующему
"своему" элементу массива с учетом числа процессоров. В D17 содержится
текущее значение адреса a0+ih+jNh = (D15)+j(D16),
используемое для автоматической переадресации при последовательном ( j = 0,1,...)
обращении к дескриптору. При этом предполагается начальное обращение (при j =
0 ) к "своему" элементу массива и последующее изменение адреса элемента
на величину Nh, хранимую в D16.
в памяти расположены в смежных ячейках), D12 — количество k-1 элементов, D13 — адрес последнего
( a2k-4 ) элемента массива. Элемент D14 служит для организации автоматической переадресации при
последовательном обращении к данному массиву. В D14 хранится адрес a0+jh для выборки
элемента массива при j -м ( j = 0,1,...) обращении к
нему ( j может быть
параметром цикла). После выполнения обращения этот адрес увеличивается на
шаг h, т.е. выполняется операция (D14) :=
(D14)+(D11). Следующая группа
дескрипторных элементов предназначена для автоматического распределения
элементов массива между процессорами. В D15 содержится адрес a0+ih, где i — номер процессора. Таким образом, каждый процессор
формирует собственное
значение D15, располагая адресом регистра в своей памяти,
содержащего значение i, для начального обращения к "своему"
элементу массива. В D16 содержится значение Nh, используемое для
переадресации к следующему
"своему" элементу массива с учетом числа процессоров. В D17 содержится
текущее значение адреса a0+ih+jNh = (D15)+j(D16),
используемое для автоматической переадресации при последовательном ( j = 0,1,...)
обращении к дескриптору. При этом предполагается начальное обращение (при j =
0 ) к "своему" элементу массива и последующее изменение адреса элемента
на величину Nh, хранимую в D16.
Сформируем дескриптор D2 = {D20,...,D27} для массива {ak,...,a2k-2} = {a10,...,a18}. Отличие элементов этого дескриптора от элементов дескриптора D1 определяется другими значениями адресов первого и последнего элементов массива, а также шагом h = 1.
В табл.12.1 представлена программа счета.
По команде 0 производится синхронизация системы для одновременного выполнения следующей команды. По данной команде каждый процессор посылает в блок C сигнал. Обратный сигнал, по которому процессор приступает к выполнению следующей команды, приходит в том случае, если все процессоры при выполнении данной команды послали сигнал в C. Выполнение команды СИНХ повторяется до получения сигнала от C.
| №k | КОП | I1 | A1 | I2 | A2 | I3 | A3 |
|---|---|---|---|---|---|---|---|
| 0 | СИНХ | ||||||
| 1 | ПРАД | D15 | D25 | 007 | |||
| 2 | ЗАКРА | D27 | |||||
| 3 | x | D17 | D17 | 001 | D27 | ||
| 4 | УЗАП | D27 | D23 | M | |||
| 5 | ИЗМАД | D17 | D27 | 001 | |||
| 6 | БП | 002 | |||||
| 7 | В |
По команде 1 (ПРоверка АДреса) адрес, записанный в дескрипторном элементе D15, сравнивается с адресом, записанным в дескрипторном элементе D13, а адрес, записанный в дескрипторном элементе D25, сравнивается с адресом, записанным в D23. (Команда допускает одновременно два сравнения, но может быть предусмотрено лишь одно.) Если (D15) > (D13) или (D25) > (D23), производится переход на выполнение команды, номер которой указан по третьему адресу. В противном случае выполняется следующая команда. С помощью команды ПРАД в данном случае проверяется, принадлежат ли адреса, на которые первоначально "смотрит" процессор, множеству адресов элементов массива. В примере при N > 9 результат проверки положителен для процессоров i = 0,1,...,8. Это позволяет автоматически исключать остальные процессоры из счета; на них выполняется переход на конец программы. При N = 4 все процессоры приступают к выполнению следующей команды.
По команде 2 (ЗАКРыть Адрес) адрес, записанный в дескрипторном элементе D27, заносится в ПЗА. При первом выполнении на процессоре 0 (D27) = a10, на процессоре 3 (D27) = a13.
По команде 3 выполняется операция умножения двух элементов массива. При первом выполнении команды на i -м процессоре и при данном значении k в дескрипторном элементе D17 находится адрес a0+2i, в D27 — адрес a10+i. Так как по A2 задано смещение, то сформируется адрес a0+2i+1. Таким образом, на процессоре 0 сформируется исполнительный вид команды xa0a1a10, на процессоре 1 — xa2a3a11 ит.д. После выполнения команды и записи результатов в память адреса a10,...,a13 исключаются из ПЗА. Очевидно, что при N > [k/2] в исполнительном виде команды 3, сформированной на процессорах [k/2],...,N-1, используются ранее закрытые другими процессорами адреса. Попытка выполнения этой команды, точнее, считывание по закрытым адресам, будет циклически возобновляться до тех пор, пока процессоры, закрывшие адреса, не выполнят умножение и не зашлют по этим адресам промежуточные результаты. Так реализуется управление потоком данных.
По команде 4 (Условная ЗАПись) в случае (D27) = (D23) производится считывание по адресу, указанному в дескрипторном элементе D27, и запись по третьему адресу команды ( M — модификатор, в котором указан адрес результата произведения всех элементов массива). Напомним, что в D23 указан адрес того элемента расширенного массива, в котором при счете способом "пирамиды" образуется окончательный результат.
По команде 5 (ИЗМенение АДреса) выполняются операции (D17) := (D17)+(D16) ; (D27) := (D27)+(D26). В данном примере (D16) = 8, (D26) = 4. Выполнение каждой операции сопровождается анализом — не превосходит ли вновь найденное значение адреса последнего элемента массива, указанное соответственно в дескрипторных элементах D13 и D23. Если превосходит, управление передается на окончание выполнения программы.
Команда 6 — команда Быстрого Перехода на выполнение команды2, т.е. на повторное выполнение цикла попарного умножения элементов массива. В нашем примере следующий исполнительный вид команды 3 на процессоре 0 — xa8a9a14, на процессоре 1 — xa10a11a15 ит.д.
Выход за пределы массивов при повторном выполнении команды 5 приведет к окончанию счета на процессорах 1, 2 и 3. Процессор 0 по команде 4 произведет запись окончательного результата по адресу, указанному в модификаторе 0. Третье выполнение команды 5 на процессоре 0 приведет к окончанию счета и на нем.
Команда 7 является командой Возврата при обращении к данной программе как к процедуре. По этой команде одновременно с возвратом в программу, из которой было выполнено обращение, производится коррекция указателя вершины стека вложенных процедур.

