Асинхронная ВС на принципах "data flow"

Виртуализация ресурса

Как говорилось выше, при программировании используются виртуальные адреса процессорных элементов в том случае, когда надо "назвать" промежуточные результаты счета. Эти адреса можно рассматривать как адреса некоторой условной памяти, где каждой записи соответствует единственное считывание, после чего адрес может быть переиспользован.

В общем случае произвольный объем программ при ограниченном ресурсе, в том числе объеме буферов, затрудняет статическое планирование динамического использования буферов вычислителей. Составляемая программа должна быть инвариантна относительно состава решающего поля. Одновременное независимое выполнение нескольких программ в ВС, управляемой потоком данных в мультипроцессорном и мультипрограммном режимах, требует организации многоканального доступа к совместно используемому вычислительному ресурсу, его динамического распределения. При динамическом планировании использования вычислительного ресурса коммутация вычислителей для выполнения отдельной программы может быть различной для каждой реализации в зависимости от условий совместного выполнения программ. Таким образом, возникает проблема виртуализации вычислительного ресурса, т.е. необходимость использования при программировании или трансляции условных, математических адресов вычислителей и формирования по ним физических адресов вычислителей в процессе выполнения программы на основе динамического распределения используемого ресурса.

Для составления программы в математических адресах вычислителей предположим, что мы располагаем единственным условным вычислителем с буфером, объем которого определен адресным пространством. Тег адреса может указывать на то, что этот адрес адрес вычислителя. Средствами виртуализации вычислительного ресурса в многоканальной ВС, содержащей m процессоров коммутации, являются адресный генератор АГ и таблицы соответствия TC_k, k = 1, ..., m.

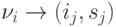Если любой из адресов (команды программы, выполняемой на k -м процессоре), является математическим адресом вычислителя, производится обращение к TC_k, состоящей из строк соответствия вида , где 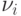— математический адрес некоторого вычислителя; (i_j,s_j) — соответствующий ему физический адрес. В случае совпадения фиксируется найденный физический адрес (i_j,s_j), а использованная строка исключается из TC_k. Необходимость исключения строки следует из того, что каждый результат вычислений используется лишь один раз. При безуспешном обращении к TC_k, АГ выдает очередной физический адрес вычислителя в порядке последовательной загрузки вычислителей решающего поля и при наличии свободных регистров в их буферах. Одновременно для данного математического адреса и найденного физического, в первом свободном регистре TC_k формируется строка соответствия.

Если по третьему адресу команды не указан математический адрес вычислителя (например, указан адрес ОПД), то АГ в порядке последовательной загрузки вычислителей формирует физический адрес вычислителя-исполнителя данной команды. По этому адресу записывается инструкция для выполнения операции, указанной в команде.

В многопроцессорной ВС адресный генератор должен быть автономным быстродействующим устройством, которое, в соответствии с последовательной загрузкой вычислителей, выдает всем процессорам одновременно адреса вычислителей для их использования при обработке адресов команд. Для ускорения его работы может быть применен метод ситуационного управления.

Метод предполагает, что в соответствии с наличием свободных регистров в каждом буфере-вычислителе и с учетом буферов, участвовавших в предыдущей выдаче, формируется новая группа адресов вычислителей. Использование этих адресов влияет на состояние буферов B_i и на определение в них новых свободных регистров, которые могут быть задействованы далее.

Принципиально возможны схемы, исключающие использование в программе коммутации адресов вычислителей для непосредственного обмена данными. В этом случае вычислители получают операнды, рассчитанные на других вычислителях, только через ОПД. Это исключает необходимость реализации механизмов виртуализации вычислительного ресурса, но увеличивает время передачи данных и частоту обращения к ОПД.

Более детально механизм виртуализации вычислительного ресурса рассмотрим на примере.

Пусть на процессорах I и II независимо выполняются программы коммутации счета значений двух выражений, преобразованных в бесскобочную запись:

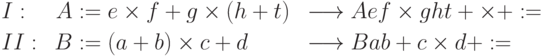
Рис. 10.6. Организация виртуального вычислительного ресурса: а — транслированные программы, б — программы при совместном выполнении

Пусть при независимом выполнении программ коммутации на двух процессорах сдвиг по времени начала их выполнения привел к тому, что команда 2 программы I выполняется одновременно с командой 1 программы II (рис. 10.6,б), за один такт работы процессора полностью обрабатывается одна команда программы. Предположим, что решающее поле содержит четыре вычислителя с номерами 1 — 4, которые используются для счета значений данных выражений.

В первом такте, начиная загрузку буферов вычислителей, АГ по впервые встретившемуся математическому адресу формирует физический адрес (1, 1) вычислителя, производящего операцию умножения. В TC₁ записывается строка соответствия .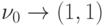

Во втором такте АГ выдает первому процессору физический адрес вычислителя (2, 1), второму — адрес (3, 1). В TC₁ формируется строка соответствия 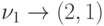, в TC₂ — .

В третьем такте с помощью на первом процессоре формируется второй адрес (2, 1), а с помощью АГ — адрес вычислителя-исполнителя (4, 1). В TC₁ формируется строка соответствия , а строка 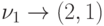уничтожается. В этом же такте с помощью на втором процессоре вместо адреса 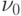формируется адрес (3, 1) (соответствующая строка уничтожается), а с помощью АГ — адрес вычислителя-исполнителя (1, 2).

В четвертом такте с помощью TC₁ формируются первый и второй адреса на первом процессоре, а с помощью TC₂ — первый адрес на втором процессоре. Для выполнения команд АГ выделит вычислители (2, 2) и (3, 2), которые должны будут отправить результаты вычислений по адресам A и B соответственно.

Представим пример программы выполнения операции "свертки массива", т.е. преобразования вида "вектор-скаляр". В нем отражены индексация и виртуализация вычислительного ресурса.

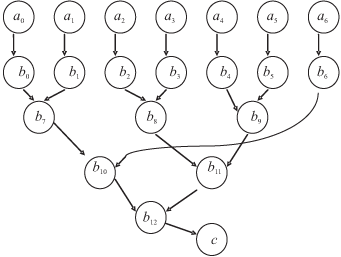
Построим программу нахождения максимального элемента в массиве,

c = max {a₁, a₂, ..., a_m\}.

Пусть b_i — математические адреса ПЭ. По ним будут автоматически формироваться пары ( номер ПЭ, номер регистра его буфера ). ПЭ будут выполнять предполагаемые операции и хранить их результаты. Математические (виртуальные) адреса ПЭ принадлежат некоторой области адресного пространства или могут сопровождаться признаком или тегом.

Тогда план вычислений для m = 7 может быть таким, как показано на рис. 10.7.

Рис. 10.7. Схема параллельной "свёртки" массива

Программа без пояснений приведена на рис. 10.8.

Рис. 10.8. Программы нахождения максимального элемента в массиве: а — с традиционным набором команд, б — с использованием групповой операции

Как видно из рисунка, принципиально просто реализуются базирование, индексация и выполнение векторных операций.