Лекция 6: Оптимальное потактовое расписание выполнения работ в многофункциональном арифметическо-логическом устройстве
Оптимизированная компоновка "длинных" командных слов
При оптимизированной компоновке "длинных" командных слов необходимо более полно задавать информацию о частичной упорядоченности работ, обусловленной графом на рис. 6.2. То есть необходимо использовать полное описание этого графа. При решении задач параллельного программирования для этого используются квадратные (размер m равен числу трехадресных команд линейного участка) нуль — единичные матрицы следования S, дополненные столбцами весов — времен выполнения работ. Такая матрица для нашего примера представлена на рис. 6.3. При этом работы, отраженные в графе, мы заменили номерами соответствующих трехадресных команд в таблице 6.1. Иначе говоря, мы можем забыть про изображение графа, а воспользоваться лишь программой в трехадресных командах.
Тогда, по аналогии с (6.11), если при совместном анализе двух команд
( i -й и j -й, i>j ) первый или второй
адрес "нижней" команды совпадает с третьим
адресом "верхней" команды, то элемент матрицы S на пересечении i -й строки и j -го
столбца полагается равным единице  , в противном
случае он равен нулю.
, в противном
случае он равен нулю.
Матрица следования ациклических графов всегда, выбором нумерации работ, может быть сведена к треугольной, что показано на рисунке выделением диагональных элементов.
Чтобы установить приоритеты работ для оптимизации расписания их выполнения, выберем значение времени, заведомо не меньшее времени их совокупного выполнения. Таким временем может быть суммарное время выполнения всех работ линейного участка или длина критического пути.
Выбрав необходимую верхнюю оценку Т времени выполнения линейного участка, рассматривая эту оценку как директивный срок, найдем поздние сроки начала выполнения работ. Алгоритм нахождения этих сроков и алгоритм нахождения суммарного объема работ, следующих каждой работе (будем называть такой объем работ объемом последующих работ), приведены ниже.
Алгоритм нахождения поздних сроков  начала выполнения работ по треугольной матрице следования.
начала выполнения работ по треугольной матрице следования.
- Производим циклический обзор справа налево столбцов матрицы S, пусть j — очередной из необработанных еще столбцов. Если все столбцы обработаны, выполнение алгоритма заканчивается.
- Если j -й столбец не содержит единичных элементов, полагаем
 . Переходим к выполнению шага 1.
. Переходим к выполнению шага 1. - Если j -й столбец содержит единичные элементы, выбираем
элементы
 множества
множества  , соответствующие
номерам единичных элементов j-го столбца.
, соответствующие
номерам единичных элементов j-го столбца. - Полагаем
 .
Выполняем шаг 1.
.
Выполняем шаг 1.
Алгоритм нахождения объемов  последующих работ. Этот алгоритм содержит две
части. В первой части производится дополнение матрицы следования всеми
транзитивными связями, позволяющими зафиксировать полную фактическую
упорядоченность работ. Вторая часть содержит нахождение указанных объемов.
последующих работ. Этот алгоритм содержит две
части. В первой части производится дополнение матрицы следования всеми
транзитивными связями, позволяющими зафиксировать полную фактическую
упорядоченность работ. Вторая часть содержит нахождение указанных объемов.
Алгоритм нахождения транзитивных связей.
- Организуем просмотр сверху вниз строк матрицы следования S.
- В очередной i -й строке организуем просмотр элементов в порядке увеличения j номеров столбцов, j < i.
- Если (i, j) = 1, изменяем строку i ее сложением со строкой j по операции дизъюнкции.
Алгоритм нахождения объемов работ.
- Организуем просмотр справа налево столбцов j матрицы следования S.
- Находим множество {i} единичных элементов j -го столбца. Находим

На рис. 6.3 даны значения величин, найденные по приведенным алгоритмам, однако транзитивные связи не указаны, чтобы избежать загромождения рисунка.
Теперь можем считать, что сформирована вся исходная информация для оптимизированной компоновки "длинных" командных слов.
Алгоритм 2 оптимизированной компоновки "длинных" командных слов.
- Формируем группу команд считывания. Исключаем команды считывания из записи программы в трехадресных командах.
- Полагаем t = 0 ( t — модельное время, номер такта).
- Полагаем t := t +1. Приступаем к компоновке очередного командного слова.
- Уменьшаем на единицу значения всех счетчиков времени команд, ранее назначенных (условно) на выполнение, т.е. включенных в командные слова ранее. Если назначения команд еще не было, переходим к шагу 6.
- Исключаем из матрицы следования S строки и столбцы, соответствующие тем трехадресным командам, для которых значения счетчиков стали нулевыми.
- Находим множество R нулевых строк матрицы следования S, соответствующих некоторой группе трехадресных команд с нулевыми значениями счетчиков времени выполнения (т.е. не назначенных ранее).
-
7. Выполняем непосредственно компоновку очередного командного слова, стремясь заполнить все его позиции:
записываем в первую позицию команду сложения с максимальным значением среди подобных команд сложения в R. Если с таким значением имеется более одной команды, из них выбирается команда с максимальным значением
 В
случае успешной записи, "взводим" счетчик тактов выполнения "назначенной"
команды. Команду исключаем из R.
В
случае успешной записи, "взводим" счетчик тактов выполнения "назначенной"
команды. Команду исключаем из R.То же пытаемся сделать с каждой позицией "длинного" командного слова.
Возможно получение "пустых" командных слов, требующих пропуска такта ( NOP — no operation) из-за неготовности операндов.
- Проверяем:
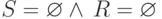 ? Т.е. не
остались ли не "назначенные" команды? Если
остались — переходим к выполнению шага 2, если нет — компоновка
"длинных" командных слов линейного участка завершена.
? Т.е. не
остались ли не "назначенные" команды? Если
остались — переходим к выполнению шага 2, если нет — компоновка
"длинных" командных слов линейного участка завершена.
Сведем в таблицу 6.5, по тактам выполнения, действия процесса формирования программы в "длинных" командных словах по рассматриваемому примеру. "Взведение" счетчиков отмечает те такты — номера "длинных" команд, — которым эти команды соответствуют. Для краткости не будем каждый раз изображать изменяющуюся матрицу следования, приведенную на рис. 6.3 в первоначальном виде, со всей сопутствующей информацией. Сформированная программа в "длинных" командных словах приведена в таблице 6.6. Начальная пересылка данных опущена.
| Такты | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение строки и столбца из матрицы S | ||||||||||||||
| 8 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||
| 9 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||
| 10 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 11 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||
| 12 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||
| 13 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 14 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 15 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 16 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 17 | 2 | 1 | 0 | Исключение ... | |||||||||||||||||
| 18 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 19 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 20 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 21 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||
| 22 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||
| 23 | 2 | 1 | 0 | Исключение ... | |||||||||||||||||
| 24 | 1 | 0 | Исключение ... | ||||||||||||||||||
| 25 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Искл. | ||||||||||||
| 26 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Искл. | ||||||||||||
| 27 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||
| 28 | 3 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||
| 29 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Искл. | ||||||||||||
| 30 | 2 | 1 | 0 | ||||||||||||||||||
| 31 | 2 | 1 | |||||||||||||||||||
| 32 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | ||||||||||||||
| 33 | 2 | 1 | 0 | Исключение ... | |||||||||||||||||
| 34 | |||||||||||||||||||||
| 35 | 2 | 1 | 0 | Искл. | |||||||||||||||||
| 36 | |||||||||||||||||||||
| 37 | |||||||||||||||||||||
| 38 | |||||||||||||||||||||
| 39 | |||||||||||||||||||||
| 40 | |||||||||||||||||||||
| 41 | |||||||||||||||||||||
| Такты | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | Исключение ... | |||||||||||||||||||||
| 31 | 0 | Исключение ... | ||||||||||||||||||||
| 32 | 0 | Исключение ... | ||||||||||||||||||||
| 34 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||||
| 36 | 2 | 1 | 0 | Исключение ... | ||||||||||||||||||
| 37 | 1 | 0 | Исключение ... | |||||||||||||||||||
| 38 | 3 | 2 | 1 | 0 | Исключение ... | |||||||||||||||||
| 39 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Исключение ... | |||||||||||||
| 40 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||||||||||
| 41 | 1 | |||||||||||||||||||||
Оптимизированная программа, как и программа, полученная в результате "быстрой" компоновки, в нашем примере планирует 40 тактов процессора. Специально выбран пример с высокой связностью работ, чтобы проверить правильность алгоритмов. Любая архитектура выявляет возможность распараллеливания лишь в том случае, если эта возможность существует.

