Характеристические числа графов и их применение в конструкторском проектировании РЭС
18.3. Плоские графы
При проектировании электрических соединений печатных плат к печатному монтажу предъявляются требования полного отсутствия или минимального числа пересечений проводников при однослойном (многослойном) печатном монтаже. Будем интерпретировать рисунок электрических соединений графом, вершины которого соответствуют контактным площадкам и переходам из слоя в слой, а рёбра - печатным проводникам платы. Для выполнения указанных требований необходимо, чтобы граф (частичные графы, представляющие отдельные слои коммутаций многослойных печатных плат) полностью размещался на плоскости, а его рёбра пересекались только в вершинах при минимизации числа вершин, соответствующих контактным переходам, т.е. граф (частичные графы) должен быть плоским. В связи с этим задача определения планарности графа и построения его плоского изображения приобретает особое значение.
Граф  называют плоским (планарным) тогда и только тогда, когда он имеет геометрическую реализацию в двухмерном евклидовом пространстве, т.е. может быть расположен на плоскости так, что все его рёбра пересекаются только в вершинах
называют плоским (планарным) тогда и только тогда, когда он имеет геометрическую реализацию в двухмерном евклидовом пространстве, т.е. может быть расположен на плоскости так, что все его рёбра пересекаются только в вершинах  графа.
графа.
Геометрическая реализация графа в евклидовой плоскости, если она вообще возможна, имеет место лишь при определённом расположении его вершин и рёбер на плоскости.
Критерии планарности графов
При исследовании принципиальной электрической схемы радиоэлектронного устройства, с точки зрения возможности её реализации с помощью печатного монтажа, конструктору важно знать ответ на следующие вопросы:
- является ли граф, соответствующий рассматриваемой принципиальной схеме, плоским;
- если граф плоский, то как получить его изображение на плоскости без пересечения рёбер?
Ответим на эти вопросы.
Прежде всего, определим максимально возможное число рёбер плоского графа.
Пусть, задан граф 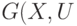 ), имеющий гамильтонов цикл. С помощью изоморфных преобразований перейдём к графу
), имеющий гамильтонов цикл. С помощью изоморфных преобразований перейдём к графу  , в котором рёбра гамильтонова цикла не пересекаются. Тогда во внутренней и внешней областях выпуклой фигуры, образованной рёбрами гамильтонова цикла
, в котором рёбра гамильтонова цикла не пересекаются. Тогда во внутренней и внешней областях выпуклой фигуры, образованной рёбрами гамильтонова цикла  , можно пронести без пересечений не более
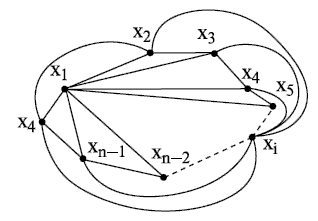
, можно пронести без пересечений не более 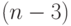 рёбер. Это показано на рис. 18.3.
рёбер. Это показано на рис. 18.3.
Следовательно, максимальное число некратных рёбер у плоского графа
 |
( n - 2) ) |
Кроме того, если известно, что число некратных рёбер графа

то такой граф заведомо плоский.
Таким образом, можно записать следующие условия для предварительного исследования планарности графа:
Разбиение графа на плоские суграфы
Если граф  неплоский, то для его геометрической реализации удаляют из
неплоский, то для его геометрической реализации удаляют из  отдельные рёбра
отдельные рёбра 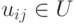 (переносят на другую плоскость). Минимальное число рёбер, которое необходимо удалить из графа для его плоского изображения, называют числом планарности графа
(переносят на другую плоскость). Минимальное число рёбер, которое необходимо удалить из графа для его плоского изображения, называют числом планарности графа 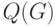 .
.
При вынесении этих рёбер на вторую плоскость получают частичный граф (суграф), состоящий из 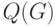 рёбер, который может также оказаться неплоским. Тогда вновь решают задачу вынесения отдельных рёбер на следующую плоскость и так далее.
рёбер, который может также оказаться неплоским. Тогда вновь решают задачу вынесения отдельных рёбер на следующую плоскость и так далее.
Минимальное число плоскостей  , при котором граф
, при котором граф  разбивается на плоские суграфы
разбивается на плоские суграфы  , называется толщиной графа
, называется толщиной графа  .
.
Наибольший интерес представляет разбиение 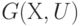 на плоские суграфы, когда переходы между плоскостями осуществляют только по вершинам графа (по ножкам конструктивных элементов, установленных на плате).
на плоские суграфы, когда переходы между плоскостями осуществляют только по вершинам графа (по ножкам конструктивных элементов, установленных на плате).
При использовании в современной аппаратуре двусторонних печатных плат важное значение приобретает задача поиска критерия бипланарности произвольного графа, т.е. возможности разбиения его на два плоских суграфа.
Па практике при разработке конструкции РЭС на печатных платах возможны два случая:
- Местоположение конструктивных элементов на печатной плате заранее неизвестно, и его требуется определить, минимизировав либо число перемычек, выполняемых в местах пересечения печатных проводников при однослойном монтаже, либо число слоёв коммутации при использовании многослойных печатных плат.
Представив схему электрических соединений конструктивных элементов в виде неориентированного графа
 , переходят к поиску рационального расположения вершин и ребер
, переходят к поиску рационального расположения вершин и ребер  на плоскости, обеспечивающему минимум пересечений рёбер графа. Найденное взаимное расположение вершин графа будет соответствовать рациональному размещению элементов па плате, а число удаляемых рёбер - необходимому числу перемычек или электрических цепей, переносимых из первого слоя во второй.
на плоскости, обеспечивающему минимум пересечений рёбер графа. Найденное взаимное расположение вершин графа будет соответствовать рациональному размещению элементов па плате, а число удаляемых рёбер - необходимому числу перемычек или электрических цепей, переносимых из первого слоя во второй. - Местоположение конструктивных элементов получено на предыдущем этапе размещения. Требуется найти рациональное расположение рёбер графа
 , интерпретирующего схему электрических соединений, при котором суммарная длина и общее число пересечений рёбер
, интерпретирующего схему электрических соединений, при котором суммарная длина и общее число пересечений рёбер  минимальны.
минимальны.
Могут применяться и другие критерии оптимизации трассировки печатных проводников.
18.4. Представление конструкции РЭС с помощью графов
При анализе конструкций РЭА применяют в основном ненаправленные графы. Принципиальная электрическая схема интерпретируется графом, в котором каждому конструктивному элементу ставятся в однозначное соответствие вершины, а электрическим связям - ребра графа. Это позволяет абстрагироваться от конкретных схем и перейти к их математическим - графам, разрабатывать эффективные методы поиска оптимальных конструктивных решений.
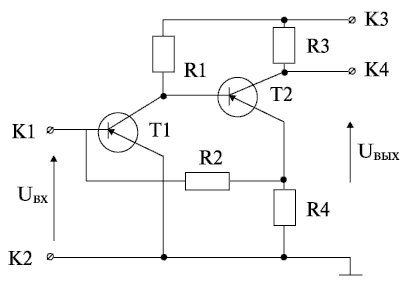
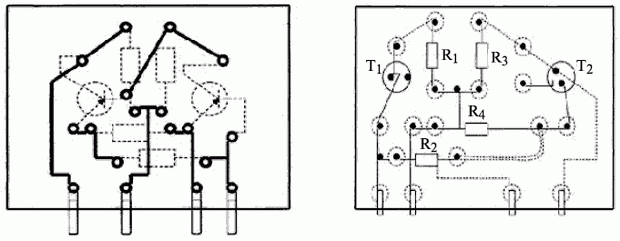
Рассмотрим схему транзисторного усилителя (рис. 18.4).
Представим конструкцию в виде произвольного неориентированного графа  , у которого
, у которого

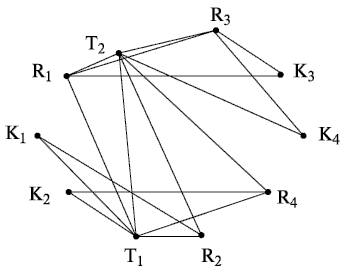
a  - множество всех электрических связей элементов конструкции (рис. 18.5).
- множество всех электрических связей элементов конструкции (рис. 18.5).
Представим конструкцию в виде произвольного неориентированного графа  , у которого
, у которого 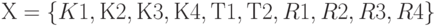 , a
, a  - множество всех электрических связей элементов конструкции.
- множество всех электрических связей элементов конструкции.
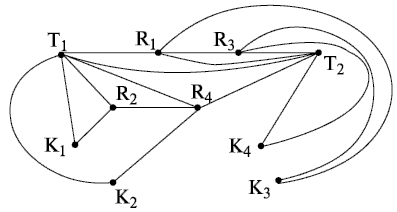
Выводим клеммы 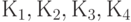 таким образом, чтобы вывести их как бы на отдельную плату - клеммник. Тогда произвольный неориентированный граф, изображённый на рис. 18.5, примет вид (рис. 18.6).
таким образом, чтобы вывести их как бы на отдельную плату - клеммник. Тогда произвольный неориентированный граф, изображённый на рис. 18.5, примет вид (рис. 18.6).
Выполним изоморфные преобразования, используя в качестве целевой функции минимум числа пересечений рёбер графа, вложенного в плоскость.
Смещаем вершины графа в фиксированные позиции на плоскости. Отдельные вершины графа могут быть предварительно закреплены, исходя из конструктивных соображений. В нашем случае такими вершинами являются клеммы  и
и 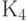 , взаимное местоположение которых определяется контактами разъёма.
, взаимное местоположение которых определяется контактами разъёма.
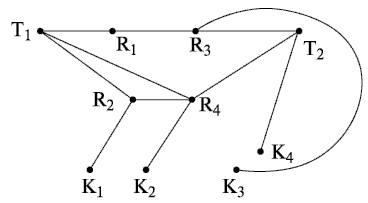
Далее исключаем те из дублирующих рёбер, которые имеют максимальную протяжённость или большее число пересечений с другими рёбрами. Далее исключаем те из дублирующих рёбер, которые имеют максимальную протяжённость или большее число пересечений с другими рёбрами (рис. 18.7).
Найденное в результате преобразования местоположение вершин графа (рис. 18.7) соответствует рациональному взаимному расположению элементов на плате. На рис. 18.8 представлен общий вид платы после трассировки.
Рассмотренный пример иллюстрирует основные принципы интерпретации принципиальной электрической схемы неориентированным графом. Далее показано выполнение над графом операций удаления отдельных рёбер и изоморфных преобразований, направленных на оптимизацию размещения элементов на печатной плате. От полученного в результате этих преобразований графа переходят к рациональному размещению элементов схемы на коммутационном поле модуля.
Контрольные вопросы
- Что называют цикломатическим числом графа?
- Как используется цикломатическое число при рассмотрении конструкции печатной платы?
- Что называют хроматическим числом графа?
- Что представляет собой бихроматический граф?
- Какой граф называют критическим?
- Показать, как используется хроматическое число графа при решении задач конструкторского проектирования РЭС.
- Что представляют собой плоские графы?
- Как используются плоские графы при печатном монтаже?
- Показать, как осуществляется переход от электрической схемы к графу.

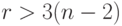 - граф заведомо
- граф заведомо 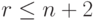 - граф заведомо плоский .
- граф заведомо плоский .