Математические методы описания моделей конструкций РЭС. Элементы теории графов

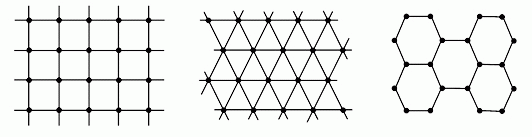
Примеры бесконечных однородных графов (рис. 17.3).

Рис. 17.3. Бесконечные однородные графы

Бесконечные однородные графы находят широкое применение в задачах трассировки печатных соединений, т.к. их использование позволяет разбивать коммутационное поле печатных плат на элементарные ячейки одинаковой формы.

Существенной характеристикой графа является его связность.

Граф, любая пара вершин которого связана, называют связным графом. В связном графе, перемещаясь по рёбрам из вершины в вершину, можно попасть в каждую вершину. Граф, состоящий из отдельных фрагментов, называют несвязным, состоящим из отдельных компонент связности.

Если граф не связный, то множество его вершин можно единственным образом разделить на непересекающиеся подмножества, каждое из которых содержит все связанные между собой вершины и вместе с инцидентными им рёбрами образует связный подграф.

Таким образом, несвязный граф представляет собой совокупность отдельных частей (подграфов), называемых компонентами связности (рис. 17.4).

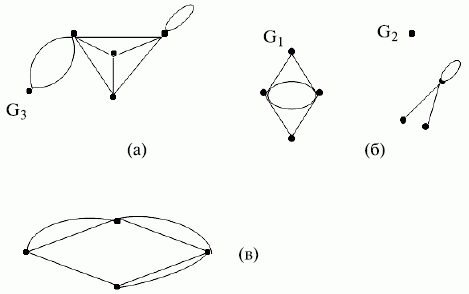
Рис. 17.4. а) связный граф; б) несвязный граф, состоящий из трех компонентов связности (G_{1}, G_{2}, G_{3}); в) сильносвязный граф, все вершины которого попарно смежны

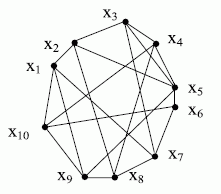
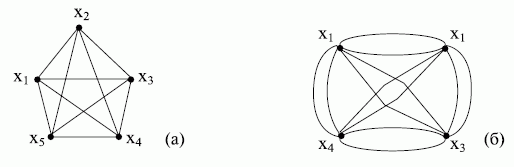
Граф, все вершины которого попарно смежны, называют сильносвязным или полным графом (рис. 17.5).

Рис. 17.5. Примеры сильносвязных графов

Полный граф, у которого при каждой вершине имеется петля, называют плотным графом.

Дадим определения маршрута, цепи и цикла.

Последовательность рёбер заданных парами вершин вида

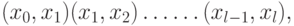
в которой любые два соседних ребра смежные, называется маршрутом.

Число рёбер в маршруте определяет его длину. Если все рёбра в маршруте различны, то такой маршрут является цепью.

Если в цепи нет повторяющихся вершин, кроме соседних, то такая цепь называется простой.

Циклом называют последовательность рёбер

при которой в результате обхода вершин графа 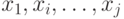по этим рёбрам возвращаются в исходную вершину .

Каждое ребро графа встречается в цикле не более одного раза, в то время как вершины могут повторяться и несколько раз.

Цикл считают простым, если в нём нет повторяющихся вершин, и сложным, если такие имеются.

Цикл называют элементарным, если он не содержит в себе никаких других циклов.

Цикл считают минимальным, если он включает минимальное число рёбер, и максимальным, если он содержит максимальное число рёбер графа.

Таким образом, цикл - это замкнутая цепь.

Рис. 17.6. Исходный связный граф

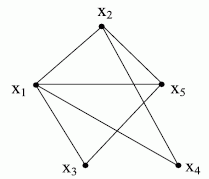
Рассмотрим граф, изображённый на рис. 17.6.

Для этого графа имеем:

• маршрут: ;
• простую цепь: ;
• простой цикл: .

Из сказанного выше можно дать ещё одно определение для связных вершин: две вершины 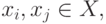графа 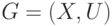называются связными, если их можно соединить маршрутом.

Большое значение в задачах конструкторского проектирования РЭС имеют эйлеровы и гамильтоновы циклы.

Эйлеров цикл - это цикл, в котором содержатся все рёбра графа.

Граф, имеющий такой цикл, называют эйлеровым графом. Эйлеров граф изображён на рис. 17.7.

Рис. 17.7. Пример эйлерова графа

Необходимым и достаточным условием наличия в конечном связном графе эйлерова цикла является чётность степеней всех его вершин.

Задача отыскания эйлерова цикла имеет большое прикладное значение.

Считают, что граф имеет гамильтонов цикл, если сумма локальных степеней двух любых вершин графа больше или равна числу вершин, т.е.

Задача отыскания гамильтонова цикла в графе также имеет большое прикладное значение, например, для отыскания и построения плоского изображения графа при решении коммутационных задач.

Гамильтонов цикл определяют для конечных связных графов аналогичным образом, но только по отношению к вершинам: цикл называют гамильтоновым, если он проходит через каждую вершину один раз.

Рис. 17.8. Пример гамильтонова цикла

Несмотря на некоторое сходство в определениях эйлеровых и гамильтоновых циклов, используемые для их отыскания методы имеют мало что общего. Критерий существования эйлерова цикла был установлен просто, для гамильтонова цикла такого общего правила не известно. Более того, иногда для конкретного графа бывает затруднительно сказать, имеет ли он такой цикл или нет. Существуют лишь частные критерии наличия в графе гамильтонова цикла.

При размещении графа в виде геометрической фигуры существует большая свобода в размещении вершин графа в пространстве и выборе формы соединяющих их рёбер ( дуг ). Следовательно, один и тот же граф может иметь различную геометрическую реализацию.

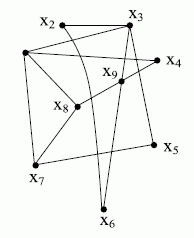
Два графа и 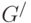изоморфны, если они имеют одинаковое число вершин и если каждой паре вершин, соединённых ребром ( дугой ), в одном графе, соответствует такая же пара вершин, соединённых ребром ( дугой ), в другом графе (рис. 17.9)

Решение ряда задач конструкторского проектирования РЭА связано с изоморфными преобразованиями графа, т.е. с построением графа, изоморфного заданному. Например, с целью сокращения числа пересечений рёбер графа, изображённого на плоскости, уменьшения суммарной длинны рёбер графа.

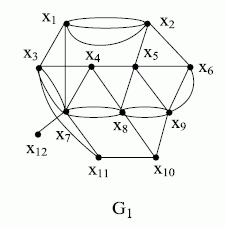
Граф, у которого существует хотя бы одна пара вершин, соединённая рёбрами ( дугами в одном направлении), называют мультиграфом (рис. 17.10). Ребра ( дуги ), связывающие одну и ту же пару вершин, считают кратными, а максимальное число кратных рёбер ( дуг ) в графе - мультичислом графа.

Для мультиграфа на рис. 17.10 мультичисло равно трём.

Рис. 17.9. Пример изоморфных графов

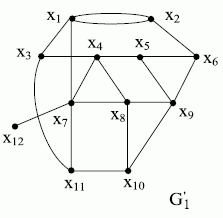
Если в графе 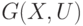опущены некоторые рёбра, а число вершин осталось прежним, то полученный граф G(X, Г) называют частичным графом 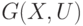. На рис. 17.11 показан частичный граф мультиграфа рис. 17.10.

Рис. 17.10. Пример мультиграфа G_1

Рис. 17.11. Частичный граф мультиграфа G_1