Математические модели (ММ) на различных иерархических уровнях
Математические модели с использованием сетей Петри
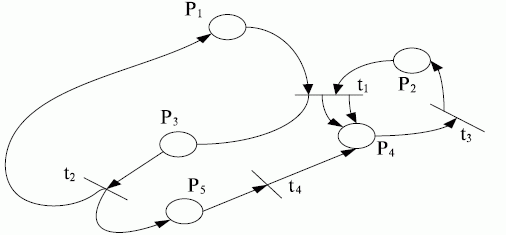
Сети Петри являются эффективным инструментом дискретных процессов. Их особенность заключается в возможности отображения параллелизма, асинхронности и иерархичности.
На рис. 13.3 приводится сеть Петри, где 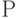 - конечное непустое множество позиций (состояний);
- конечное непустое множество позиций (состояний);  - конечное непустое множество переходов (событий), причем
- конечное непустое множество переходов (событий), причем 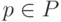 и
и 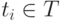 ;
;  ;
;  - функции входных и выходных инциденций;
- функции входных и выходных инциденций;  - начальная маркировка. Вершины сети
- начальная маркировка. Вершины сети 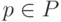 изображены кружками, а вершины
изображены кружками, а вершины 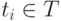 - черточками (баркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции
- черточками (баркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции 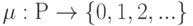 . Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переход
. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переход  может сработать при маркировке
может сработать при маркировке  , если он является возбужденным:
, если он является возбужденным:
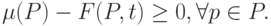 |
( 13.10) |
Данное условие показывает, что в каждой входной позиции перехода  число маркеров не меньше веса дуги, соединяющей эту позицию с переходом.
В результате срабатывания перехода
число маркеров не меньше веса дуги, соединяющей эту позицию с переходом.
В результате срабатывания перехода  , удовлетворяющего условию (13.10), маркировку
, удовлетворяющего условию (13.10), маркировку  заменяют маркировкой
заменяют маркировкой 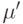 по следующему правилу:
по следующему правилу:
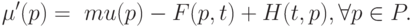 |
( 13.11) |
Это означает, что маркировка 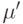 непосредственно достижима из маркировки
непосредственно достижима из маркировки  . Функционирование сети Петри - последовательная смена маркировок в результате срабатывания возбужденных переходов.
. Функционирование сети Петри - последовательная смена маркировок в результате срабатывания возбужденных переходов.
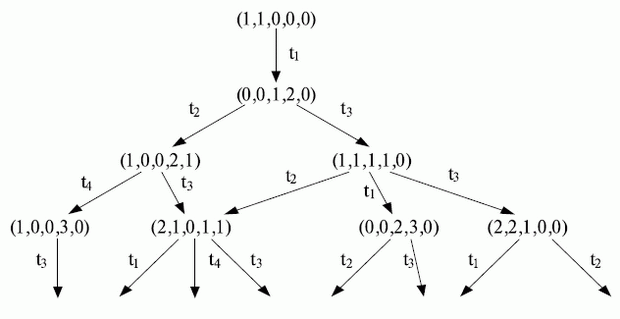
Состояние сети в данный момент времени определяется ее текущей маркировкой. Важная характеристика сети Петри - граф достижимости, с помощью которого описываются возможные варианты функционирования сети.
Такой граф имеет вершины, которые являются возможными маркировками. Маркировки  и
и 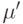 соединяются в направлении
соединяются в направлении  дугой, помеченной символами перехода
дугой, помеченной символами перехода 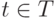 или
или  . Маркировка
. Маркировка 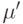 такая последовательность переходов:
такая последовательность переходов: 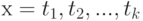 является достижимой из маркировки
является достижимой из маркировки  , если существует, что
, если существует, что  .
.
В качестве примера рассмотрим сеть Петри, изображенную на рис. 13.3
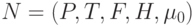 , где
, где 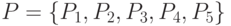 ;
;
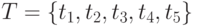 ;
; 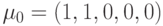 . Функции
. Функции  и
и  заданы матрицами:
заданы матрицами:
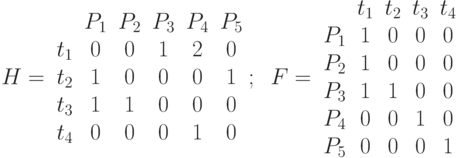
Фрагмент графа достижимости для сети Петри приведен на рис. 13.4.
13.3. Структурные модели
Структурные, или структурно-логические, модели подразделяются на табличные, сетевые и перестановочные. Сетевые определяются строками булевой матрицы.
![[S_i\times F(S)] =
\begin{array}{ccccc}
F_g& F_a& F_\lambda& F_n& \\
1& 1&1&1&S_1\\
1& 1&1&0&S_2\\
1& 1&0&1&S_3\\
1& 1&0&0&S_4\\
1&0&1&0&S_5\\
1& 0&0&0&S_6\\
0& 1&1&1&S_7\\
0& 1&1&0&S_8\\
0& 1&0&1&S_9\\
0& 1&0&0&S_{10}\\
0& 0&1&0&S_{11}\\
0& 0&0&0&S_{12}\\
\end{array}](/sites/default/files/tex_cache/e6246111582d1ab33b4795c9ebaf516c.png)
Здесь  - свойства моделей, влияющих на содержание проектирования;
- свойства моделей, влияющих на содержание проектирования;  - набор свойств, если все графы объектов А_{к}, проектируемых по данной модели, простые пути или цепи,
- набор свойств, если все графы объектов А_{к}, проектируемых по данной модели, простые пути или цепи, 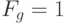 и
и 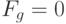 в противном случае;
в противном случае; 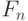 - набор свойств, учитывающих число элементов во всех вариантах объектов
- набор свойств, учитывающих число элементов во всех вариантах объектов 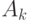 .
.
(  - число элементов во всех
- число элементов во всех 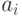 одинаково ,
одинаково , 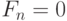 - в противном случае);
- в противном случае); 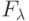 - набор свойств, учитывающих отношения между любыми элементами объекта
- набор свойств, учитывающих отношения между любыми элементами объекта 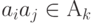 во всех вариантах объектов
во всех вариантах объектов  (
( 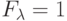 - отношение не меняется,
- отношение не меняется, 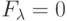 - в противном случае);
- в противном случае); 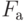 - набор свойств, учитывающих состав элементов
- набор свойств, учитывающих состав элементов 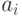 в
в  (
( 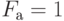 - состав одинаков,
- состав одинаков, 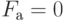 в противном случае).
в противном случае).
В матрице (13.2) модели класса 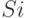 называют табличными. В табличной модели каждому набору свойств
называют табличными. В табличной модели каждому набору свойств 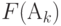 соответствует единственный вариант проектируемого объекта
соответствует единственный вариант проектируемого объекта  , поэтому табличные модели используют для поиска стандартных, типовых и готовых решений.
Модели остальных классов применяют для получения типовых унифицированных и индивидуальных проектных решений при наличии их вариантов и необходимости оптимизации решения. Модели классов
, поэтому табличные модели используют для поиска стандартных, типовых и готовых решений.
Модели остальных классов применяют для получения типовых унифицированных и индивидуальных проектных решений при наличии их вариантов и необходимости оптимизации решения. Модели классов 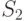 ,
, 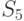 ,
, 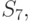
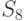 И
И 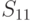 называют сетевыми .Структура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В этой модели может содержаться несколько вариантов проектируемого объекта
называют сетевыми .Структура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В этой модели может содержаться несколько вариантов проектируемого объекта  , однако во всех вариантах сохраняется неизменным соотношение порядка между входящими элементами. Модели классов
, однако во всех вариантах сохраняется неизменным соотношение порядка между входящими элементами. Модели классов 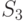 ,
, 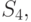
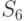 ,
, 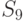
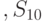 и
и 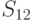 называют перестановоч
ными.Соотношение порядка между эл
ементами проектируемого объекта
называют перестановоч
ными.Соотношение порядка между эл
ементами проектируемого объекта  в перестановочных объектах обычно задается с помощью графа, содержащего ориентировочные циклы, причем все варианты объектов
в перестановочных объектах обычно задается с помощью графа, содержащего ориентировочные циклы, причем все варианты объектов  , проектируемые по перестановочным моделям, различаются порядком между элементами, входящими в них.
, проектируемые по перестановочным моделям, различаются порядком между элементами, входящими в них.
Объектом проектирования  может быть технологический процесс, операция или технологический переход. Если рассматривать технологический процесс в качестве объекта проектирования, то операции будут элементами. При проектировании операции элементами будут технологические переходы.
может быть технологический процесс, операция или технологический переход. Если рассматривать технологический процесс в качестве объекта проектирования, то операции будут элементами. При проектировании операции элементами будут технологические переходы.
Если 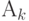 должен содержать фиксированный набор элементов
должен содержать фиксированный набор элементов 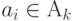 ,то
,то
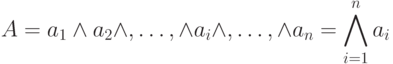
если 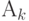 может содержать любой элемент
может содержать любой элемент  ,то
,то
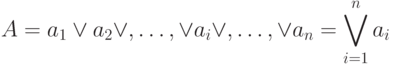
если какой-либо единственный элемент  ,то
,то
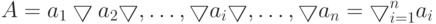
При разработке группы элементов с помощью табличной модели устанавливается последовательность этой разработки. Каждый элемент имеет варианты 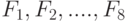 с определенными свойствами, поэтому состав свойств вариантов, относящихся к группе элементов, будет
с определенными свойствами, поэтому состав свойств вариантов, относящихся к группе элементов, будет

Если ввести совокупность свойств более высокого уровня:
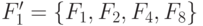 , то получим
, то получим
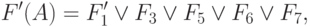
а если совокупность свойств элементов 1, 2, 3-й групп (соответственно, элементам  ,
, 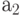 ,
,  группы
группы  деталей, т.е.
деталей, т.е. 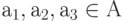 ), то получим
), то получим
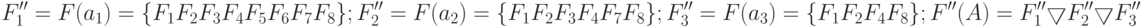
Контрольные вопросы
- В чем сущность блочно-иерархического подхода к проектированию?
- Как составляется полная модель?
- Что характерно для макромодели?
- Что представляют собой сети Петри?
- Какие модели называют табличными?
- Для чего используют табличные модели?
- Что называется сетевой моделью?
- Как описывается структура сетевых моделей?
- Что называется перестановочной моделью?