Статистическое моделирование

3.13. Модель противоборства как процесс блуждания по решетке

Итак, чтобы построить имитационную модель, надо скопировать и описать в виде программы элементарные действия процесса и соединить их в нужной последовательности. Такое прямолинейное моделирование, в общем, понятно и естественно.

Однако, иногда можно увидеть совсем неожиданную аналогию (структурную или функциональную) между исследуемым процессом и некоторым другим, на первый взгляд ничего не имеющим общего с оригиналом. Имитационная модель этого нового процесса может оказаться проще и, тем не менее, позволит определить искомые характеристики.

В частности, для исследования процесса противоборства двух сторон таким "дублером" может быть процесс "блуждания частицы по решетке".

Рассмотрим, как перемещение некоторого объекта по решетке становится аналогом, моделью противоборства двух сторон, если целью моделирования является определение оценок численностей сторон в конце операции - интервала исследования.

Противоборствуют две стороны: и .

Первоначальные численности сторон: и .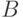

Текущие численности сторон: 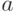и ; , .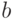

Время "жизни" каждого средства случайно, имеет экспоненциальное распределение с параметрами и 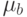сторон и .

Обе стороны образуют единую систему . В ходе боя численности сторон изменяются (уменьшаются) или остаются неизменными. Мы это трактуем как переход системы из одного состояния в другое: или и т. д.

Граф состояний такой системы имеет вид двумерной целочисленной решетки с однонаправленными связями. Переходу системы из одного состояния в другое можно поставить в соответствие случайное блуждание некоторой частицы по решетчатой структуре. Отсюда и название моделирующей абстракции.

Граф состояний приведен на рис. 3.26.

увеличить изображение
Рис. 3.26. Граф состояний моделируемой системы противоборства Исходное состояние системы S_{a,b} .

Стороны ведут взаимоуничтожающий огонь. В предположении ординарности потока событий, переводящего систему из одного состояния в другое, система из состояния может перейти только лишь в состояние или (или остаться в прежнем состоянии ). Очевидно, направления переходов в графе - решетке только вправо или вниз.

Процесс противоборства заканчивается при полном уничтожении средств одной из сторон, т. е. при переходе в состояние или а также по окончании временного интервала исследования 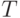. Так заканчивается одна, -я реализация процесса противоборства. Зафиксировав остатки средств сторон 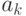и и усреднив их за реализаций, найдем решение поставленной задачи - определение оценок численностей сторон на момент окончания операции.

Продвижение времени в модели - фиксированными шагами . Величина такова, чтобы на этом временном участке происходило не более одного события.

Суммарные интенсивности огня сторон и 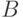зависят от численностей их боеспособных средств и равны и.

Следовательно, вероятности уничтожения одного из средств (перехода системы в очередное состояние) равны:

Эти приближенные равенства тем точнее, чем меньше .

Блок схема алгоритма ИМ противоборства двух сторон, построенная способом "блуждания частицы по решетке" представлена на рис. 3.27.

Блоки 1 и 2 - установка начальных условий на весь процесс моделирования и на каждую очередную реализацию.

Блок 3 - расчет вероятносте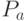й и .

Блоки 4…10 - определение исхода противоборства на очередном временном отрезке . Если , то свершилось событие , иначе - проверка условия ? Если это условие выполняется, то свершилось событие , если не выполняется, то пораженных средств не оказалось. Вероятность этого события равна .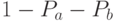

Блоки 11… 16 аналогичны соответствующим блокам предыдущей имитационной модели противоборства двух сторон (см. рис. 3.22).

Сравним обе рассмотренные модели противоборства двух сторон.

Последняя заметно проще. Упрощение связано с тем, что в ней не моделируется поведение каждого отдельного средства, а рассматривается поведение системы в целом.

Однако, первую модель несложно развить, например, учесть неоднородность средств в каждой группировке, указав соответствующие значения и .

Последняя модель таких возможностей не имеет.

увеличить изображение
Рис. 3.27. Блок-схема модели "блуждание частицы по решетке"

3.14. Типовая схема имитационной модели с продвижением времени по событиям

Уточним понятие события.

Под событием будем понимать смену состояния системы.

Виды событий:

• выход из строя технических средств;
• восстановление работоспособности техники;
• поступление сообщения на узел связи;
• начало передачи сообщения;
• конец передачи сообщения;
• уничтожение цели и т. п.

Вид события связан с типом элемента, сменяющего свои состояния. Смена состояний системой есть объединение смен состояний ее элементов.

Будем считать, что событие совершается в конкретный момент времени мгновенно.

Вообще-то событие - смена состояния - совершается за некоторый отрезок времени. Но в интересующих нас процессах длительность смены состояний много меньше времени нахождения системы в каком-либо состоянии, поэтому длительностью события можно пренебречь.

Каждому событию соответствует пространственно-временная точка , где - момент свершения события; - тип элемента системы, сменившего состояние; 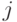- вид или номер события этого элемента.

Различают события активные и пассивные.

Активное событие - это смена состояния элемента под воздействием присущих ему внутренних причин.

Например, отказ техники - активное событие, так как оно определяется износом или скрытыми дефектами. Конец передачи сообщения по каналу связи - активное событие, так как при прочих равных условиях оно определяется быстродействием передающей аппаратуры.

Пассивное событие - событие, возникшее под воздействием активного события.

Например:

• начало передачи сообщения по каналу связи, так как оно зависит от другого активного состояния - поступления сообщения на узел связи;
• изменение числа устройств, ожидающих ремонта. Увеличение численности зависит от поступления неисправных устройств в мастерскую; уменьшение - от освобождения мастерской; и др.

В одном и том же элементе системы могут происходить активные и пассивные события. Например:

• начало решения задачи на компьютере - событие пассивное, так как оно происходит от другого события: поступления запроса на решение;
• завершение решения - событие активное, так как оно зависит от внутренних свойств компьютера (производительности);
• поступление заявок на обслуживание в очередь и покидание очереди - события пассивные, но уход из очереди "нетерпеливых" заявок - события активные.

Обычно элемент, в котором происходит активное событие, называют активным, пассивное событие - пассивным.

Основу имитационной модели системы с продвижением модельного времени по событиям составляют модели активных событий. Пассивные события моделируются просто, если выявлены их причинно-следственные отношения с активными событиями.

Множество точек представляет собой поведение системы во времени. Множество точек активных событий называется списком событий.

Список событий может быть сформирован либо перед началом моделирования, либо формироваться в ходе моделирования. На рис. 3.20 список событий представлен диаграммой ж.

Имитационная модель с продвижением времени по событиям любой системы состоит из следующих функциональных модулей:

• модуль установки начальных условий;
• модуль продвижения модельного времени;
• модули реакции;
• модуль обеспечения заданной точности и достоверности;
• модуль формирования результата моделирования.

Модуль установки начальных условий.

Модуль устанавливает значения разного рода констант, например, заданное число реализаций модели, критерий завершения интервала моделирования 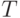и др., а также элементы списка событий - все или только начальные для каждого вида события.

Если в предыдущем способе продвижения модельного времени на фиксированные промежутки модуль состоял из трех блоков установки начальных условий, то здесь достаточно двух: установка начальных условий на весь процесс моделирования ( 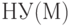) и установка начальных условий на каждую реализацию ( ).

Модуль продвижения модельного времени. Его функции: выбор в списке событий момента времени свершения очередного,

ближайшего события , и фиксация очередного момента модельного времени:

Модули реакции. Представляют собой программы, имитирующие действия соответствующих активных событий и связанных с ними пассивных событий. Модулей реакции столько, сколько возможно в системе активных событий. Подключение того или иного модуля реакции происходит в соответствии с значениями и .

Помимо имитации событий в модулях реакции могут выполняться следующие действия:

• фиксация текущих значений параметров, интересующих исследователя, так называемых числовых атрибутов, и, возможно, их текущая статистическая обработка;
• подсчет числа свершившихся событий данного вида;
• прогноз времени свершения , очередного события данного вида и занесение этого времени в список событий (если список событий формируется в ходе моделирования). Прогноз осуществляется с помощью соответствующего датчика случайных чисел, адекватно имитирующего временные интервалы между событиями.

Модуль обеспечения заданной точности и достоверности ведет подсчет числа реализаций модели . При достижении моделирование заканчивается.

Модуль формирования результата. Выполняет окончательную статистическую обработку данных моделирования и обеспечивает отображение результата в данном виде.

Взаимодействие модулей показано на рис. 3.28.

Переход на соответствующий модуль реакции , 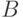и т. д. происходит по значению индекса текущего значения .

увеличить изображение
Рис. 3.28. Блок-схема модели с продвижением времени по событиям

Безусловный выход из любого модуля реакции - в блок выбора очередного значения модуля продвижения времени.

В общий цикл предлагаемой структуры моделирующего алгоритма удобно вписывается определение конца интервала исследования 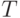и момента конца моделирования ( ) . Для этого вся система интерпретируется как один обобщенный активный элемент, имеющий два состояния: включен и выключен.

В списке событий этому обобщенному элементу соответствует одна пространственно-временная точка . Здесь - начальная точка отсчета интервала исследования, обычно . Когда в процессе работы моделирующего алгоритма окажется, что , управление будет передано специальному модулю реакции , который зафиксирует конец текущей реализации .

Этот модуль также в случае передаст управление блоку ( ) на выполнение очередной реализации, а в случае выполнения - модулю формирования результатов.

Ранее было отмечено, что некоторые элементы в зависимости от состояния могут быть активными либо пассивными.

В случае перехода такого элемента в пассивное состояние надо

исключить возможность выбора его блоком "Выбор ". Для этого в список событий записывается время его переключения на свой модуль реакции. В этом случае модуль продвижения времени никогда не найдет этой временной точки, так как интервал исследования будет заканчиваться раньше.

Но когда этот элемент вновь станет активным, время его активного события , должно быть занесено в список событий.