Типовые математические модели

Во многих случаях модель может быть представлена в виде конструкций из математических символов. В первой теме такие модели мы назвали аналитическими, чтобы отделить от других математических моделей - имитационных. С развитием последних область применения аналитических моделей сократилась. Однако актуальность такого моделирования сохраняется для систем, особенно тех, в которых протекают так называемые процессы без последействия. Процессы без последействия находят место при функционировании многих технических систем. Впервые один из типов такого процесса ввел в научный обиход и исследовал отечественный математик А. А. Марков, поэтому процессы без последействия и системы, в которых они протекают, названы марковскими, а один из типов такого процесса назван цепью Маркова. В настоящее время теория марковских процессов разработана широко и детально, в основном, благодаря отечественным ученым А. Я. Хинчину, Б. В. Гнеденко, А. Н. Колмогорову и другим. Популярность этой теории состоит еще и в том, что она может быть применена и к системам с последействием, которые с помощью некоторых ухищрений можно трактовать как марковские.

В этой теме рассматриваются элементы теории марковских процессов и ряд аналитических моделей, в основе которых лежит допущение о марковости протекающих в моделируемых объектах процессов. К таковым, в первую очередь, относится широкий класс самых разнообразных объектов, имеющих общее название систем массового обслуживания (СМО). Для ряда стандартных структур СМО аналитические модели, связывающие показатели эффективности СМО с характеристиками элементов СМО, приведены в соответствующих справочниках. Здесь же приводятся классификация СМО и приемы построения графов состояний СМО, позволяющих строить или применять готовые аналитические модели.

Заметим, что для ряда современных сложных СМО аналитическое моделирование неприемлемо в силу недостаточности адекватных математических средств. В этих случаях следует применять имитационное моделирование, которое детально рассматривается в следующих темах.

В многоэлементных системах с большим числом состояний аналитическое моделирование на основе теории марковских процессов становится весьма громоздким. В этом случае используется так называемый метод динамики средних, который в основе имеет также марковость процесса. Этот метод существенно упрощает аналитическое моделирование для случаев определения средних характеристик состояний моделируемой системы. В этой теме дано обоснование метода и приводятся примеры его применения.

2.1. Дискретные марковские процессы

Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.

Однако есть ряд конкретных математических схем, проверенных практикой и доказавших эффективность моделированием. Целью изучения настоящей темы является освоение таких математических моделей.

В инженерной практике часто возникает задача моделирования процессов случайной смены состояний в исследуемом объекте. В рамках нашей профессии нас интересуют дискретные состояния. Например, техническое состояние объекта может характеризоваться дискретными состояниями: исправен - неисправен, загружен - находится в простое и т. п. Численности боевых средств противоборствующих сторон изменяются дискретно, очереди объектов, ожидающих обслуживания, и многое другое.

Вид очередного состояния может определяться случайным образом, смена состояний может происходить в случайные или не случайные моменты времени.

Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова - старшего (1856-1922), выдающегося русского математика, разработавшего основы теории таких процессов.

Сущность процесса без последействия понятна из определения.

Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.

Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.

А. А. Марков имеет дополнение к фамилии "старший" потому, что его сын - тоже Андрей Андреевич Марков - выдающийся математик, специалист в области теории алгоритмов и др.

А. А. Марков - старший известен также как давший вероятностное обоснование метода наименьших квадратов, приведший одно из доказательств предельной теоремы теории вероятностей и многое другое.

Дальнейшее развитие теория марковских процессов получила в работах выдающегося отечественного математика Андрея Николаевича Колмогорова.

Марковские процессы делятся на два класса:

• дискретные марковские процессы (марковские цепи);
• непрерывные марковские процессы.

Дискретной марковской цепью называется случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.

Непрерывным марковским процессом называется случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.

Итак, моделирование на основе дискретных марковских процессов.

Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.

Система имеет возможных состояний: , , 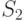..., 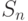. Вообще говоря, число состояний может быть бесконечным. Однако модель, как правило, строится для конечного числа состояний.

Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 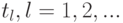В дальнейшем будем называть временные точки 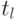шагами.

Известны вероятности перехода 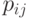системы за один шаг из состояния в состояние .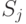

Цель моделирования: определить вероятности состояний системы после -го шага.

Обозначим эти вероятности 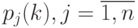(не путать с вероятностями ).

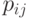Если в системе отсутствует последействие, то есть вероятности 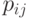не зависят от предыстории нахождения системы в состоянии , а определяются только этим состоянием, то описанная ситуация соответствует модели дискретной марковской цепи.

Марковская цепь называется однородной, если переходные вероятности 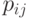от времени не зависят, то есть от шага к шагу не меняются. В противном случае, то есть если переходные вероятности 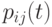зависят от времени, марковская цепь называется неоднородной.

Значения 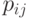обычно сводятся в матрицу переходных вероятностей:

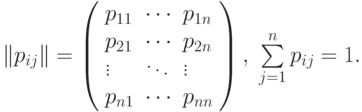
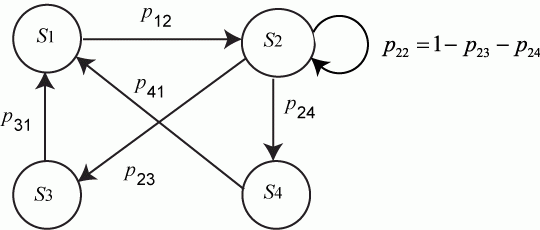
Значения 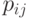могут также указываться на графе состояний системы. На рис. 2.1 показан размеченный граф для четырех состояний системы. Обычно вероятности переходов "в себя" - 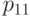, и т. д. на графе состояний можно не проставлять, так как их значения дополняют до 1 сумму переходных вероятностей, указанных на ребрах (стрелках), выходящих из данного состояния.

Не указываются также нулевые вероятности переходов. Например, на рис. 2.1 это вероятности , 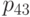и др.

Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость

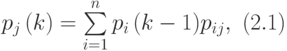
где - вероятность -го состояния системы после -го шага, ;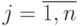

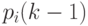- вероятность -го состояния системы после -го шага, ;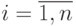

- число состояний системы;

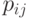- переходные вероятности.

Рис. 2.1. Размеченный граф состояний системы

Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:

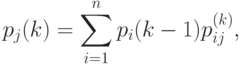
где - значения переходных вероятностей для -го шага.

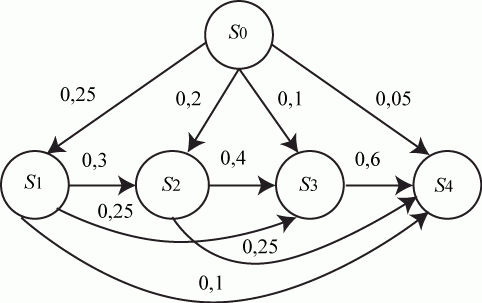
Пример 2.1. По группе из четырех объектов производится три последовательных выстрела. Найти вероятности состояний группы объектов после третьего выстрела.

Матрица переходных вероятностей имеет вид:

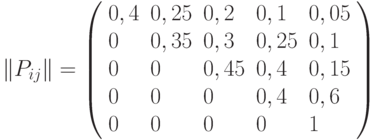
Размеченный граф состояний приведен на рис. 2.2.

Рис. 2.2. Размеченный граф состояний четырех объектов

Прежде чем приступить к вычислениям, необходимо ответить на следующие вопросы.

1. Является ли рассматриваемый процесс поражения целей марковским? Да, так как степень поражения объекта (смена его состояния) не зависит от того - когда и каким образом объект был приведен в настоящее состояние, а зависит только от его текущего состояния.
2. Подходит ли рассматриваемая задача под схему марковской цепи? Да, так как время представляет собой дискретные отрезки - время между выстрелами (шаги).
3. Процесс однородный или неоднородный? Есть основания полагать, что процесс однородный, так как переходные вероятности не зависят от времени. Кроме этого, мы полагаем, что объекты - неподвижные и во времени обстрела менять свое положение не могут (что привело бы к изменениям 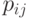после каждого выстрела).
4. И, наконец, надо правильно определить начальное состояние системы, так как от этого могут существенно зависеть результаты моделирования. В нашем случае вполне естественно считать начальным состояние - все объекты целы.

Следовательно, есть все основания для применения ранее введенного рекуррентного выражения (2.1).

Решение. Так как до первого выстрела все объекты целы, то .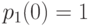

После первого выстрела все значения вероятностей 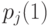соответствуют первой строке матрицы переходных вероятностей. Рассчитаем вероятности остальных состояний.

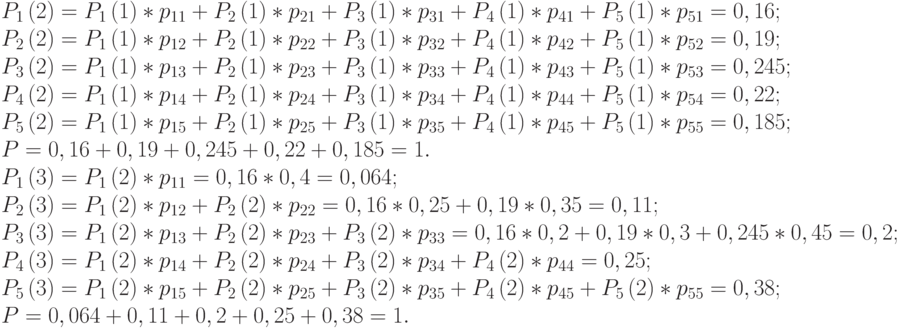
Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).

1. Зафиксировать исследуемое свойство системы.

   Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то - занятость. Если, как в примере 2.1, состояния объектов, то - поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости (2.1) определить искомые вероятности.

В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей .

При неоднородном марковском процессе переходная вероятность 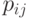представляет собой условную вероятность перехода

, зависящую от - очередного временного шага. В этом случае должны быть указаны более одной матрицы значений 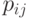(для некоторых шагов матрицы могут быть одинаковыми).

Например, при нанесении ударов по объектам, которые могут перемещаться (танковая группировка, корабли и т. п.), последние будут принимать меры по рассредоточению средств или другому защитному маневру, вплоть до активного противодействия атакующей стороне. Очевидно, все эти меры приведут к уменьшению поражающих возможностей стороны, наносящей удары, т. е. к соответствующему изменению переходных вероятностей. Процесс становится неоднородным.