|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Статистическое моделирование
Если очередным ближайшим событием окажется освобождение канала не последней фазы, то блок 5 передает управление модулю реакции В, имитирующему действия в СМО при свершении этого активного события.
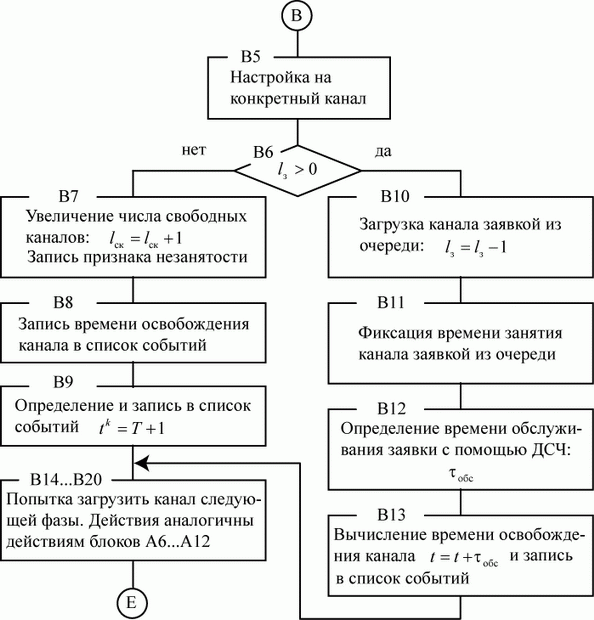
Блок-схема алгоритма модуля реакции В представлена на рис. 3.32.
Модуль В имеет две функции. Во-первых, попытаться загрузить освободившийся канал заявкой из очереди на входе фазы, в которой находится освободившийся канал. Во-вторых, имитировать продвижение заявки, освободившей канал, в следующую фазу обслуживания.
Блок В5 - настройка модуля на освободившийся канал конкретной фазы.
Каждая фаза обслуживания имеет свою очередь заявок на входе, свою очередь свободных каналов и, возможно, свои датчики случайных чисел. Поэтому не будем вводить для них новые обозначения, оставим те, которые были использованы при описании модуля А.
Блок В6. Проверка: есть ли в очереди на входе фазы заявки, ожидающие обслуживания (  ) ? Если есть, то освободившийся
) ? Если есть, то освободившийся
канал должен быть немедленно загружен (блоки 10… 13). Если нет, то канал должен быть переведен в режим ожидания (блоки В7…В9).
Блок В7. Очередь свободных каналов увеличивается на  (
( 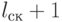 ) . Признак занятости канала устанавливается в нуль.
) . Признак занятости канала устанавливается в нуль.
Блок В8. Запоминание момента освобождения канала.
Блок В9. Перевод освободившегося канала в пассивное состояние. Для этого пространственно-временной точке  , относящейся к освободившемуся каналу, присвоить значение времени,
, относящейся к освободившемуся каналу, присвоить значение времени,
превышающего интервал исследования  , то есть
, то есть 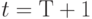 . Это значение
. Это значение  заносится в список событий. Управление передается блоку В14.
заносится в список событий. Управление передается блоку В14.
Блоки В14…В20 моделируют размещение заявки, освободившей канал, в следующей фазе обслуживания. Функции и взаимные связи этих блоков аналогичны блокам А6 … А12, рассмотренным ранее:
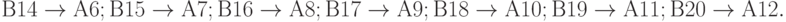
Блок 20 передает управление блоку 3 для идентификации очередного активного события. Этим событием может быть поступление заявки от какого-либо источника на вход первой фазы или окончание обслуживания заявки каким-либо каналом. В этих случаях управление будет снова передано модулям реакции  или
или  .
.
Если же очередным активным событием окажется освобождение канала последней фазы, то управление передается модулю реакции С (рис. 3.33).
Блок С5 - настройка на соответствующий канал последней фазы. Аналогичен блоку В5.
Блоки С6…С13 - загрузка освободившегося канала ожидающей заявкой, если таковая есть на входе последней фазы. Функции и взаимосвязи блоков аналогичны блокам В6…В13. Блок С6 соответствует блоку В6, блок С7 - блоку В7 и т. д. по одинаковым номерам.
Блок С14 формирует числовые атрибуты заявок, покидающих СМО. Такими атрибутами могут быть: суммарное время обслуживания заявки на всех фазах, суммарное время ожидания в очередях, число обслуживаний без ожидания и др. Атрибуты запоминаются и управление передается блоку 2.
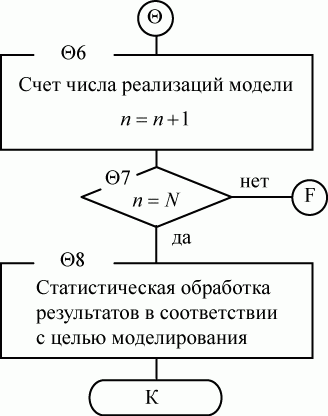
Если очередное значение 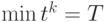 , что означает окончание интервала исследования работы СМО, управление передается модулю реакции
, что означает окончание интервала исследования работы СМО, управление передается модулю реакции  (рис. 3.34).
(рис. 3.34).
Построить имитационную модель с продвижением времени можно и по-другому. Однако рассмотренная структура модели обладает важными достоинствами:
- Моделирующий алгоритм нагляден и прост, что существенно упрощает программирование и, особенно, отладку модели, а также изучение готовых моделей.
- Рассмотренная структура алгоритма позволяет параллельно разрабатывать модель по отдельным модулям и, следовательно, сокращать время на ее создание.
Облегчены корректировка и развитие модели. Например, в рассмотренной модели СМО легко учесть выход из строя и восстановление каналов обслуживания. Для этого надо добавить два модуля реакции: один - на возникновение отказа, другой - на восстановление работоспособности. Оба эти события рассматриваются как активные, если неисправность возникает из-за внутренних дефектов оборудования, а восстановление является результатом усилий обслуживающего персонала, входящего в состав СМО.
Вопросы для самоконтроля
- Что такое имитационная статистическая модель? Сравните ее с аналитической моделью.
- Назначение датчиков случайных чисел (генераторов) в имитационном моделировании.
- Принцип формирования случайных чисел в алгоритмических датчиках случайных чисел.
- Почему случайные числа, формируемые в компьютере, являются псевдослучайными квазиравномерными?
- Формирование случайных величин с произвольными законами распределения вероятностей методом обратной функции.
- Формирование равномерно распределенных случайных чисел на произвольном отрезке
![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) .
. - Формирование нормально распределенных случайных чисел с произвольными значениями
 и
и  .
. - Найти методом обратной функции процедуру розыгрыша непрерывной случайной величины, распределенной по закону Ре-лея, заданного плотностью вероятности
 при
при  ;
; 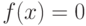 при
при  .
. - Найти процедуру розыгрыша случайной величины, распределенной по закону Вейбулла, заданного плотностью вероятности
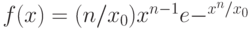 при
при  ;
; 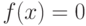 при
при  .
. - Создать программу мультипликативного датчика равномерно распределенных случайных чисел для 64-разрядной сетки:
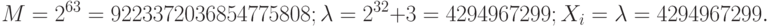
Определить период повторения случайных чисел.
- Усовершенствуйте алгоритм имитационной модели (рис. 3.5) так, чтобы можно было определять не только оценку математического ожидания вероятности поражения объекта, но оценку математического ожидания расхода ракет.
- Способ моделирования единичных событий.
- Способы моделирования полной группы несовместных событий.
- Три способа моделирования совместных независимых событий.
- Моделирование совместных зависимых событий.
- Стационарный и нестационарный случайные процессы.
- Эргодический и неэргодический случайные процессы.
- Способы продвижения модельного времени в имитационной модели.
- Какие виды времени различают при имитационном моделировании?
- Что понимается под распределенным имитационным моделированием? Сравните его с последовательным имитационным моделированием.
- Что значит квазипараллельное моделирование?
- Модель противоборства, назначение блоков. Признаки окончания одной реализации.
- Поясните прием моделирования противоборства двух сторон методом "блуждания по решетке".
- Понятие активного и пассивного элемента в модели СМО.
- Блок-схема имитационной модели СМО.
- Модули реакции в модели СМО.
- Достоинства структуры модели СМО.