НОУ ИНТУИТ | Компьютерное моделирование. Лекция 4: Статистическое моделирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 16.11.2010 | Доступ: свободный | Студентов: 5154 / 2848 | Оценка: 4.43 / 4.14 | Длительность: 27:21:00

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

Теги: анализ, имитационные модели, модели, GPSS World, синтез

|

Вам нравится? Нравится 50 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

3.4. Моделирование равномерно распределенной случайной величины

Особое значение в статистическом моделировании имеет непрерывная равномерно распределенная случайная величина. Особая значимость этой случайной величины объясняется тем, что, во-первых, она сама по себе необходима для моделирования случайных процессов и величин и, во-вторых, случайные величины с другими законами распределения формируются на их основе.

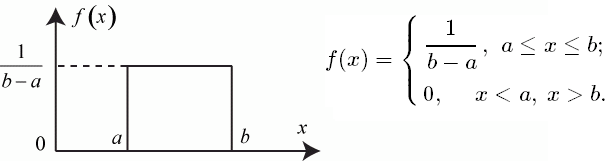
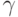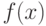Определение. Непрерывная случайная величина $\gamma$ имеет равномерное распределение в интервале [a, b] , если ее плотность вероятности f(x) определяется так (рис. 3.9):

Рис. 3.9. Плотность вероятности равномерного распределения

Значения характеристик равномерного закона распределения:

математическое ожидание $M [ \gamma ] =\cfrac{a+b}{2}$ ;
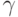дисперсия $D[ \gamma] =\cfrac{(b-a)^2}{12}$ .

При моделировании часто используются случайные числа из интервала [0,1] . Непрерывная случайная величина $\gamma$ равномерно распределена в интервале [0,1] , если:

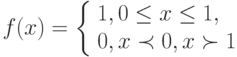
$f(x) =\left \{\begin{array}{l} 1,0\le x\le 1,\\ 0,x\prec 0,x\succ 1 \end{array}$

В этом случае $M[ \gamma ] =\cfrac{1}{2},D[ \gamma ] =\cfrac{1}{12}$ .

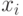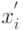Случайное число $x_{i}$ из интервала [0,1] легко преобразуется в случайное число $x_{i}^{'}$ для интервала [a, b] :

$x_{i}^{?} = (b - a)\cdot x_{i} + a .$

Применительно к двоичным дробям случайное число из интервала [0,1] представляет собой бесконечную дробь:

$\gamma=z_1\cdot 2^{-1}+z_2\cdot 2^{-2}+\ldots z_i\cdot 2^{-i}+\ldots;\,\,i=\overline{1,\infty} \\ z_i =\left \{\begin{array}{ll} 1,& p=0.5,\\ 0,& p=0.5 \end{array}$

Очевидно, реализовать такую дробь в компьютере невозможно, так как разрядная сетка компьютера ограничена. В компьютере можно формировать дискретные последовательности случайных чисел, которые не могут отличаться друг от друга только на величину меньше 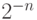$2^{-n}$ ( - число разрядов в сетке компьютера). То есть непрерывного, "теоретического" распределения на компьютерах получить нельзя. Если эти числа равновероятны, то такое распределение случайных чисел называют квазиравномерным.

Заметим, что непрерывные случайные величины существуют только в теории. На практике все случайные величины дискретны и шаг дискретности равен наименьшей единице измерения.

Случайная величина 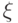$\xi$ , имеющая квазиравномерное распределение в интервале [0,1] , принимает значения

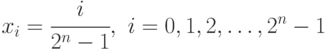
$x_i=\cfrac{i}{2^n-1},\,\, i =0,1,2,\ldots,2^n-1$

с вероятностями 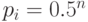$p_{i} =0.5^n$ .

Можно показать, что эта случайная величина имеет характеристики:

$M[\xi]=\cfrac{1}{2},\,\,D[\xi]=\cfrac{1\cdot(2^n+1)} {12\cdot(2^n-1)}.$

( 2^n-1)})

Современные компьютеры имеют разрядность не менее 32. Следовательно, $М[ \xi ] =М[ \gamma ]$ , а дисперсии тоже практически совпадают. Учитывая это, в дальнейшем квазиравномерное распределение будем называть равномерным и обозначать: $\gamma \sim Rav[0, 1]$ .

Для формирования последовательности случайных чисел в компьютере может использоваться один из трех основных способов:

аппаратный (физический);
табличный (файловый);
алгоритмический (программный).

Аппаратный способ. При этом способе случайные числа формируются специальным устройством. Источником случайных чисел чаще всего являются шумы в электронных приборах. Временные расстояния между шумовыми всплесками, превышающими подобранный уровень ограничения, фиксируются как случайные числа из распределения $\gamma \sim Rav[0, 1]$ .

Преимущества такого способа:

количество случайных чисел неограниченно;
не требует затрат оперативной памяти;
требует малые вычислительные ресурсы компьютера.

Однако, такой датчик (генератор) случайных чисел имеет существенные недостатки, которые в настоящее время исключили его из инженерной практики:

трудность настройки;
необходимость периодической проверки формируемой последовательности на соответствие закону распределения;
обеспечение стабильности условий работы устройства - питания, влажности, температуры, старения приборов и элементов;
при необходимости невозможно повторить эксперимент при одной и той же последовательности случайных чисел.

Табличный способ. Случайные числа в виде таблицы (файла) помещаются в оперативную или внешнюю память компьютера. Эти числа формируются заранее или берутся из соответствующего справочника. Достоинствами такого способа являются:

числа требуют однократную проверку при формировании или недоверии источнику;
можно повторять вычислительный эксперимент при одной и той же последовательности случайных чисел.

Недостатки же очень существенны:

количество случайных чисел ограничено;
файл занимает место в оперативной памяти компьютера;
при размещении во внешней памяти обращение за случайными числами увеличивает время моделирования.

Алгоритмический способ. При этом способе случайные числа формируются с помощью специальных алгоритмов (формул) и реализующих их программ при каждом обращении моделирующего алгоритма за случайным числом. Достоинства способа:

в настоящее время предлагается достаточно алгоритмов, генерирующих случайные числа, проверенных практикой и, следовательно, не нуждающихся в особых проверках;
можно многократно воспроизвести одну и ту же последовательность;
в памяти компьютера хранится только программа датчика (генератора), занимающая, как правило, малый объем;
алгоритмический датчик может быть реализован и аппа-ратно, за счет чего существенно сокращается время формирования случайного числа и в целом время моделирования.

Недостатки:

на формирование случайного числа при программной реализации датчика требуются затраты машинного времени;
любой алгоритмический датчик может сгенерировать ограниченное количество неповторяющихся чисел.

В настоящее время практически везде применяются алгоритмические датчики случайных чисел (ДСЧ). Создание высокопроизводительных компьютеров существенно снижает роль первого недостатка (затраты машинного времени). Второй недостаток устраняется использованием в одной модели нескольких ДСЧ.

Алгоритмические датчики не обеспечивают получение теоретически "чистой" случайности чисел, так как их формирование идет по формулам. Вследствие этого, рано или поздно последовательность случайных чисел станет повторяться или выродится. Последнее означает, что, начиная с некоторого числа, все последующие числа будут равны нулю.

Поэтому алгоритмические датчики называют датчиками псевдослучайных чисел. Современные датчики вырабатывают числа, псевдослучайность которых практически неощутима.

Качество алгоритмического датчика оценивается тем, насколько полно он удовлетворяет следующим требованиям:

закон распределения формируемых чисел должен быть равномерным (квазиравномерным);
числа должны быть статистически независимыми;
числа не должны повторяться;
формирование чисел должно занимать минимальное машинное время и минимальный объем памяти.

Понимая, что алгоритмический ДСЧ выдает детерминированную, псевдослучайную последовательность квазиравномерно распределенных случайных чисел, в дальнейшем будем называть его датчиком случайных равномерно распределенных чисел.

Исторически первым таким датчиком является датчик, в котором был реализован так называемый "способ срединных квадратов". Сущность способа заключается в следующем:

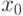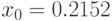подбирается начальное число $x_{0}$ , например, $x_{0} = 0.2152$ ;
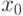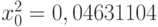вычисляется квадрат $x_{0}$ : $x _{0}^{2} = 0,04631104$ ;
первое случайное число 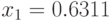$x _{1} = 0.6311$ , то есть середина $x _{0}^{2}$ ;
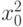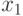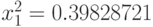вычисляется квадрат $x _{1}$ : $x _{1}^{2} = 0.39828721$ ;
второе случайное число 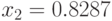$x_{2} = 0.8287$ и т. д.

Такие ДСЧ теперь не используются: между числами имеется сильная корреляция, случайность отсутствует, при неудачно выбранном 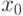$x_{0}$ последовательность может быстро выродится, то есть 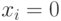$x_{i} =0$ при $i \succ i^*$ .

В настоящее время очень широкое распространение в практике моделирования получил мультипликативный метод формирования случайной последовательности:

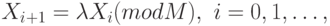
$X_{i} _{+1} = \lambda X_i (modM),\,\, i = 0,1,\ldots ,$

где 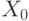$X_{0}$ - произвольное нечетное число, неотрицательное;

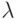$\lambda$ - коэффициент, 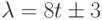$\lambda = 8t \pm 3$ , - любое целое положительное число;

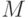- значение модуля. Для реализации на компьютере удобно M = p^q , где 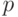- основание системы счисления (2 или 10), 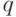- число разрядов в случайном числе.

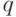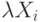В этом случае взятие числа по модулю сводится к выделению младших разрядов произведения $\lambda X_{i}$ .

Алгоритм мультипликативного метода

Выбрать 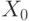$X_{0}$ , например,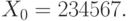 $X_{0} = 234567.$
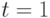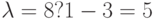Вычислить коэффициент $\lambda$ . Пусть , тогда $\lambda = 8?1-3 = 5$ .
Выбрать модуль 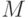. Пусть система счисления десятичная ( 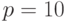), разрядность случайных чисел .
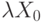Вычислить произведение $\lambda X_{0}$ : $\lambda X_{0} = 5\cdot 234567 = 1172835$ .
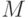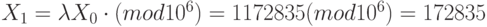Найти остаток от деления по модулю : $X_{1} = \lambda X_{0}\cdot (mod10^6) = 1172835(mod10^6) = 172835$ .
Найти число последовательности случайных чисел из интервала : $x_{1}=X_{1}/10^6 = 0.172835$ .
Присвоить $X_{0} = X_{1}$ и перейти к п. 4.

Рассмотренный метод обеспечивает приемлемое качество случайных чисел в смысле равномерности распределения и их независимости, а также простой реализации на компьютере.

Применяется и немного более сложный алгоритм:

$X_{i} _{+1} = ( \lambda X_{i} +\mu )(modM), i = 0,1,\ldots ,$

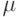где $\mu$ - неотрицательное целое число.

Такой метод называется конгруэнтно-мультипликативным. При удачном подборе дополнительного параметра 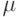$\mu$ корреляция

формируемых чисел может быть несколько уменьшена по сравнению с мультипликативным методом.

Дальше >>

Авторизоваться

Компьютерное моделирование

Статистическое моделирование

3.4. Моделирование равномерно распределенной случайной величины

Вопросы и ответы