|
приветствую создателей курса и благодарю за доступ к информации! понимаю, что это уже никто не исправит, но, возможно, будут следующие версии и было бы неплохо дать расшифровку сокращений имен регистров итд, дабы закрепить понимание их роли в общем процессе. |
Процессоры цифровой обработки сигналов
Процессоры цифровой обработки сигналов
Процессоры цифровой обработки сигналов представляют собой класс специализированных микропроцессоров, предназначенных для решения задач цифровой обработки сигналов (ЦОС), к которым относятся обработка звуковых сигналов, обработка изображений, распознавание речи, распознавание образов, цифровая фильтрация, спектральный анализ и др.
Часто в литературе такие микропроцессоры называются цифровыми сигнальными процессорами (ЦСП), или DSP ( Digital Signal Processors ).
Первые процессоры этого класса появились в конце 1970-х годов. Требования практики, связанные с широким развитием мобильной беспроводной связи, стационарных систем широкополосной связи, использованием цифровой обработки сигналов в бытовой аудио- и видеотехнике и устройствах компьютерной периферии, с одной стороны и колоссальный прогресс электронной промышленности с другой привели к тому, что к настоящему времени производительность ЦСП возросла до сотен миллионов операций в секунду, а цена упала более чем на 90 % и даже для самых мощных процессоров составляет в настоящее время менее $20. Низкая потребляемая мощность (менее 1 Вт на максимальной частоте работы процессора) обеспечивает их широкое использование в различных встраиваемых устройствах от бытовой электроники до бортовых систем специального назначения.
Цифровая обработка сигналов - это арифметическая обработка последовательности значений амплитуд сигнала, получаемых через равные промежутки времени. Главное, что отличает эту информацию, - она необязательно заносится в память и поэтому может оказаться недоступной в будущем. Следовательно, обрабатывать ее нужно в реальном масштабе времени (РМВ).
К основным особенностям цифровой обработки сигналов, которые во многом определяют архитектуру процессоров DSP, относятся:
- поточный характер обработки больших объемов данных в РМВ;
- обеспечение возможности интенсивного обмена с внешними устройствами.
Для эффективной реализации алгоритмов цифровой обработки сигналов необходима аппаратная поддержка базовых операций ЦОС. Поэтому рассмотрим вначале принципы цифровой обработки сигналов, оказывающие особое влияние на архитектуру ЦСП.
Любой аналоговый сигнал можно представить в виде характеристик -либо амплитуда-время, либо частота-амплитуда. Для перехода от одной формы представления к другой используется преобразование Фурье. Операции, выполняющие это преобразование, являются базовыми в цифровой обработке сигналов.
Преобразование Фурье представляет собой в общем случае работу с некоторой непрерывной функцией. С непрерывным преобразованием Фурье удобно работать в теории, но на практике мы обычно имеем дело с дискретными данными. Для обработки звуковых и видеосигналов в компьютере они сначала преобразуются в цифровую форму и представляются в виде некоторого набора отсчетов частот и амплитуд, производимых через определенные промежутки времени (период дискретизации). Поэтому здесь стоит говорить не об интегральном, а о дискретном преобразовании Фурье (ДПФ).
Пусть дана конечная последовательность чисел x0, x1, x2, ..., xN-1 (в общем случае комплексных). Дискретное преобразование Фурье заключается в поиске другой последовательности X0, X1, X2, ..., XN-1, элементы которой вычисляются по формуле:
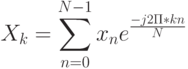 |
( 16.1) |
Пусть дана конечная последовательность чисел X0, X1, X2, ..., XN-1 (в общем случае комплексных). Обратное дискретное преобразование Фурье заключается в поиске другой последовательности x0, x1, x2, ..., xN-1, эле менты которой вычисляются по формуле:
 |
( 16.2) |
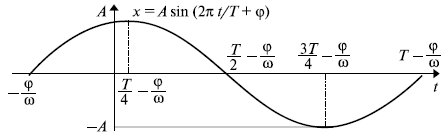
В общем случае гармоническое колебание, которое имеет вид, пред ставленный на рис. 16.1, описывается следующим выражением:
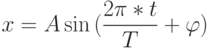 |
( 16.3) |
Где A 0 - амплитуда сигнала, Т - его период,  - сдвиг фазы сигнала.
- сдвиг фазы сигнала.
Это колебание можно описать также выражением:
 |
( 16.4) |
где 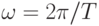 - круговая частота сигнала. Данное выражение будем называть гармоникой.
- круговая частота сигнала. Данное выражение будем называть гармоникой.
Преобразуем последнее выражение к виду:
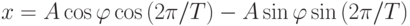 |
( 16.5) |
Выделим в (16.5) элементы, независимые от t, и обозначим их как Re и Im. В результате получим:
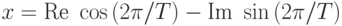
где 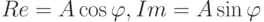
По величинам Re и Im можно однозначно восстановить амплитуду и фазу исходной гармоники:
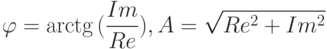 |
( 16.6) |
Разложим каждое комплексное число Xk из выражения обратного преобразования Фурье (16.2) на мнимую и действительную составляющие 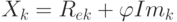 , а экспоненту - по формуле Эйлера на синус и косинус действительного аргумента. Получим:
, а экспоненту - по формуле Эйлера на синус и косинус действительного аргумента. Получим:
![x_n=\sum_{k=0}^{N-1}[\frac{Re_{k}}{N}\cos{(\frac{2\pi{k}n}{N})}-\frac{Im_k}{N}
\sin{(\frac{2\pi{k}n}{N})}]+
i\sum_{k=0}^{N-1}[\frac{Re_{k}}{N}\sin{(\frac{2\pi{k}n}{N})}-\frac{Im_k}{N}
\cos{(\frac{2\pi{k}n}{N})}]](/sites/default/files/tex_cache/0bce9ea7547d32a4055aef6567f774b8.png) |
( 16.7) |