Q. Некоторые доказательства

Это приложение содержит некоторые доказательства для теорем, используемых в лекции 2 курса "Математика криптографии и теория шифрования" и "лекции 1" . Почти все они короткие и неформальные. Они рассчитаны на студентов, изучающих курс криптографии. Читатель, заинтересованный в более детальном изучении, может пополнить свои знания из книг, посвященных теории чисел.

Q.1. Лекция 2

Эта лекция содержит некоторые доказательства теорем по теории делимости, евклидовых алгоритмов и сравнений.

Теория делимости

Ниже - доказательства нескольких теорем по теории делимости.

Теорема Q.I:Уравнение деления (алгоритм)

Для целого числа a и b, где b > 0, существуют целые числа q и r, такие, что

a = q x b + r.

Доказательство:

Рассмотрим арифметическую прогрессию в форме

...,-3 x b, - 2 x b, - 1 x b , 0 x b, 1 x b, 2 xb, 3 x b, ...

Очевидно, что целое число является или равным одному из членов этой прогрессии, или находится между двумя последовательными членами. Другими словами, a = q x b + r, где q x b - член в вышеупомянутой прогрессии и r - смещение от этого члена.

Теорема Q.2. Если a|1, тогда .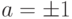

Доказательство:

a|1 ->.1 = a x x, где x - целое число.

Это означает: ( x = 1 и a = 1 ) или ( x = -1 и a = -1 ).

Поэтому: .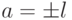

Теорема Q.3.Если a|b и b|a, тогда .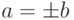

Доказательство:

a | b -> b = x x a, где x - целое число.

b |a -> = y x b, где y - целое число.

Мы имеем a =y x (x x a) = (y x x) x a. -> y x x = 1.

Это означает: ( x = 1 и y = 1 ) или ( x = -1 и y = -I ).

Поэтому: .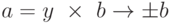

Теорема Q.4. Если a|b и b|c, тогда a|c.

Доказательство:

a | b -> b= x x a, где X - целое число.

b| c -> c = y x b, где y -целое число.

Мы имеем c = y x (x x a) = (y x x ) x a.

Поэтому a | c.

Теорема Q.5.Если a|b и a|c, тогда a|(b + c).

Доказательство:

a | b -> b = x x a, где x - целое число.

a | c -> c = y x a, где y - целое число.

Мы имеем b + c = (x + y) x a.

Поэтому a| (b + c).

Теорема Q.6. Если a |b и a | c, тогда a |(m x b + n x c), где m и n - произвольные целые числа.

Доказательство:

a |b -> b = x x a, где x - целое число.

a |c -> c = y x a, где y - целое число.

Мы имеем (m x b + n x c) = m x (x x a) +n x x (y x a)= (m x x + n xy) x a.

Поэтому a |(m x b + n x c).

Евклидовы алгоритмы

Мы использовали евклидов и расширенный евклидов алгоритмы в лекции 2. Ниже даны доказательства двух теорем, связанных с этими алгоритмами.

Теорема Q.7.Если a = b x q + r ( r - остаток от деления a на b ), то НОД (a, b) = НОД (b, r).

Доказательство

Предположим, что E - набор всех общих делителей a и b. Каждый элемент E делит a и b, поэтому он делит r = a - b x q. Это означает, что E - набор всех общих делителей a, b, и r.

Предположим, что F - набор всех общих делителей b и r. Каждый элемент F делит b и r ; поэтому делит a = b x q + r. Это означает, что F - набор всех общих делителей a, b и r.

Это означает, что E = F -> a, b и r имеют одинаковый набор общих делителей. Поэтому НОД (a, b) == НОД (b, r).

Как мы видели в "лекции 2" , эта теорема - основание евклидового алгоритма для нахождения наибольшего общего делителя двух целых чисел.

Теорема Q.8.Если a и b - целые числа и оба не равны нулю, то существуют целые числа x и y, такие, что НОД (a, b) = x x a + y x b.

Доказательство:

Предположим, что D - набор всех значений (x x a +y x b), а d есть наименьшее значение отличное от нуля.

Мы можем записать a= q x d + r -> r= a - q x d=(1 - q x x)a + (-q x y) b, где 0 <= r <= d.

Это подразумевает, что r входит в D. Но поскольку r < d, то или r = 0, или d | a.

Подобным путем мы можем показать, что d | b.

Поэтому d - общий делитель a и b.

Любой другой делитель a и b делит d = x x a+ y x b. Поэтому d должен быть НОД (a,b).

Как мы видели в "лекции 2" , эта теорема - основание расширенного евклидового алгоритма.

Сравнение

Ниже даются доказательства некоторых теорем о сравнении, используемые в лекции 2.

Теорема Q.9.Если a, b и n - целые числа и n > 0, то 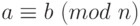, тогда и только тогда, когда существует целое число q, такое, что q x n + b.

Доказательство:

Если 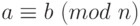, то n | (a - b), это означает, что есть целое число q, такое, что a - b = q x n.

Поэтому мы имеем a = q x n + b.

Если есть целое число q, такое, что a = q x n + b, тогда a - b = q x n, что означает n |(a - b).

Поэтому мы имеем .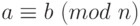

Теорема Q.10.Если a, b, c и n - целые числа при n > 0, такие, что 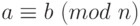, то

• .
• .
• .

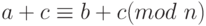Доказательство: Обратите внимание, что .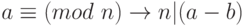

• (a+c) - (b + c) = a - b. Поскольку n |(a - b), n|(a + c) - (b + c).

  Поэтому .
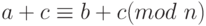• (a - c) - (b - c) = a - b. Поскольку n | (a - b), n | (a - c) - (b - c)

  Поэтому .
• (a x c) - (b x c) = (a - b) x c. Поскольку n | (a - b), n | (a - b) x c.

  Поэтому a x c = b x c (mod n).

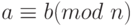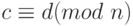Теорема Q.11.Если a, b, c, d и n - целые числа при n > 0, такие, что и , то

• .
• 
• .

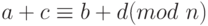Доказательство:

Обратите внимание, что ;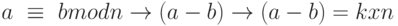

1. а .(a +c) - (b + d) = (a - b) + (c - d) = k x n + l x n = (k + l) x n.

   Поэтому .
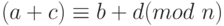2. б. (a - c) - (b - d) = (a - b) - (c - d) = k x n - l x n = (k - l ) x n.

   Поэтому .
3. a x c - (b - d) = c x (a - b) + b x (c - d) = (c x k + b x I) x n.

   Поэтому