|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
L. Сложность
L.1. Сложность алгоритма
В криптографии мы нуждаемся в инструменте для анализа вычислительной сложности алгоритма. Нам нужно, чтобы алгоритмы шифрования (или дешифрования) имели низкий уровень сложности (были эффективными). Еще условие: чтобы алгоритм, с точки зрения криптоанализа (перехвата кода), имел высокий уровень сложности (был не эффективен). Другими словами, мы хотим выполнять шифрование и дешифрование как можно быстрее, но чтобы злоумышленник при этом не смог никогда, даже с использованием компьютера, расшифровать сообщение.
Сложность алгоритма обычно базируется на двух типах ресурсов. Пространственная сложность алгоритма рассматривает объем памяти, которая должна хранить алгоритм (программу) и данные. Сложность по времени алгоритма рассматривает сумму времени, необходимую для выполнения алгоритма (программы) от начала до получения результата.
Сложность побитовой операции
В остальной части этого приложения мы будем говорить только о сложности по времени, которая имеет большее влияние на работу алгоритма, поскольку этот более общий показатель к тому же проще измерять. Сложность по времени алгоритма зависит от конкретного компьютера - того, на котором алгоритм должен быть выполнен. Чтобы сделать сложность независимой от компьютера, была определена сложность побитовой операции . f (nb), - она подсчитывает число элементарных операций, которые должен выполнить компьютер, чтобы создать результат при nb -битовом вводе. Элементарная обработка бита - это время, которое требуется компьютеру, чтобы сложить, вычитать, умножать или делить два единственных бита или сдвигать единственный бит.
Пример L.1
Какова сложность побитовой операции, которая выполняет функцию сложения двух целых чисел?
Решение
Сложность операции -. f (nb) = nb, где nb - число битов, которые представляют большое целое число. Если значение этого числа - N, то nb = log2 N.
Пример L.2
Какова сложность побитовой операции для функции, которая умножает два целых числа?
Решение
Хотя сегодня есть более быстрые алгоритмы умножения двух целых чисел, традиционно число разрядных операций предполагает, что эта сложность равна nb2. где. nb - число битов, представляющих большее целое число. Сложность поэтому -. f (nb) = nb2.
Пример L.3
Какова сложность побитовой операции для функции, складывающей два целых числа, каждое из которых содержит d десятичных цифр?
Решение
Максимальное значение множества цифр d разрядного десятичного числа.- N = 10d - 1 или. 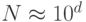 . Биты во входном слове -. nb = log2 N = log210d =, d x log 2 10. Тогда с ложность равна f (nb) = d x log 2 10. Например, если d = 300 цифр, .
. Биты во входном слове -. nb = log2 N = log210d =, d x log 2 10. Тогда с ложность равна f (nb) = d x log 2 10. Например, если d = 300 цифр, . 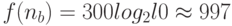 побитных операции.
побитных операции.
Пример L.4
Какова сложность побитовой операции для функции, которая вычисляет. B = AC (если A<C )?
Решение
Предположим, что число битов в C - nb. ( C = 2nb или. nb = log2C ). Обычный метод возведения в степень использует умножение числа самого на себя C раз. Каждая операция умножения нуждается в nb побитовых операций (при использовании обычного алгоритма умножения). Поэтому сложность - f(nb) = C x n2b = 2nb x nb2. Например, если C находится в диапазоне 21024 (nb = 1024), обычный метод возведения в степень имеет сложность
f(nb) = 21024 x 10242 = 21024 x (210)2 = 21044
Это означает, что если компьютер может сделать 220 (почти один миллион) побитных операций в секунду, для выполнения этой операции ему потребуется 21044 / 220 = 21024 секунд.
Пример L.5
Какова сложность побитовой операции функции, которая вычисляет B = AC (если A < C ) с использованием показательного алгоритма (метод "возведения в квадрат и умножения")?
Решение
Быстрый показательный алгоритм использует максимум 2nb умножений, где nb - число битов в двоичном представлении C. Каждый оператор умножения требует. nb2.побитных.операций. Поэтому сложность - f (nb) = 2nb x n2 = 2nb3. Например, в диапазоне 21024 (nb = 1024), быстрый показательный алгоритм дает нам
f (nb) = 2 x 10243 = 21 x (210) 3 == 231
Это означает, что если компьютер может сделать 220 (почти один миллион) операций в секунду, он затратит на выполнение этой операции 231/220 = 211 секунды (почти 34 минуты). Сегодня компьютер может выполнить эту операцию гораздо быстрее.
Асимптотическая сложность
Цель оценки сложности состоит в том, чтобы измерить поведение алгоритмов, когда число nb бит на входе является очень большим. Например, предположим, что ниже показаны оценки сложности двух алгоритмов:
f1(nb) = 5 x 2nb + 5nb и f2(nb) = 2nb + 4
Когда nb мало, эти два алгоритма ведут себя иначе, когда nb является большим (приблизительно 1000 ). В последнем случае два алгоритма ведут себя почти одинаково. Причина в том, что элементы 5, 5nb и 4 настолько малы по сравнению с элементом 2nb, что они могут полностью игнорироваться. Мы можем сказать, что для больших nb
f1(nb) = f2(nb) = 2nb. Другими словами, мы интересуемся f(nb), когда nb приближается к бесконечности.
Большие O-нотации
Применив асимптотическую сложность, мы можем определить стандартный масштаб сложности функций с дискретными значениями переменных и определить сложность алгоритма, используя одно из этих значений. Один из общих стандартов называется большой O-нотацией (Big O-Notation). В этом стандарте . f(nb) = O(g (nb)). где. g(nb) - функция nb, полученная из. f(nb) с использованием следующих трех теорем.
-
Первая теорема. Если мы можем найти константу K, такую, что f(nb) < K x g (nb),то мы имеем. f(nb) = O (g (nb)). .Эта теорема может быть легко реализована, если применить следующие два простых правила:
- a. Установите коэффициенты. nb.в функции . f(nb) на. 1.
- b. Сохраните наибольший элемент в. f(nb) как. g (nb) и удалите другие. Элементы оцениваются от наиболее низкого к самому высокому, как это показано ниже:
(1). (log nb), (nb), (nb log nb), (nb log nb log lognb), (nb2), (nb3),......, (nbk), (2nb), (nb!)
-
Вторая теорема.Если f1(nb) = O (g1 (nb)) и f2(nb) = O (g2 (nb)) ,то
f1(nb) + f2(nb)= O (g1 (nb) + g2 (nb) )
-
Третья теорема..Если f1(nb) = (g1 (nb)) и f2(nb) = O (g2 (nb)) ,то
f1(nb) f2(nb)= O (g1 (nb) g2 (nb) )
Пример L.6
Найдите большие O-нотации для . f(nb) = nb5 + 3 nb2 + 7.
Решение
Обратите внимание, что. f(nb) = nb5 + 3 nb2 + 7 nb0. Применение первого правила первой теоремы дает. g(nb) = nb5+ nb2+ 1. Применение второго правила дает нам. g(nb) = nb5..Большая O -нотация -. O (nb5).
Пример L.7
Найдите большие O-нотации для. f(nb)= (2nb + nb5) + (nb log2 nb).
Решение
Мы имеем. f1(nb)= ( 2nb+ nb5) и f2(nb) = (nb log2 nb). Поэтому g1(nb) = 2nb и g2(nb) = nb log2 nb.
Применяя вторую теорему, мы имеем g(nb)= 2nb + . nb log2 nb. Снова применяя первую теорему, мы получаем g(nb) = 2nb. Большая O -нотация - O(2nb).
Пример L.8
Найдите Большую O -нотацию для. f(nb) = nb! ( nb. факториал).
Решение
Мы знаем . nb! = nb! x (nb! - l) x....... x 2 x l. Каждый элемент имеет максимальную сложность O(nb). Согласно третьей теореме, полная сложность -. nb раз O(nb), .или. O(nbnb).
Иерархия сложности
Предыдущее обсуждение позволяет нам ранжировать алгоритмы, основанные на их сложности побитовой операции. Таблица L.1 дает общие уровни иерархии, используемые в литературе.
| Иерархия | Большая - O-нотация |
|---|---|
| Константа | O (1) |
| Логарифмическая | O (log nb) |
| Полином | O (nc). где c - константа |
| Субэкспоненциальная | O(2p(log(nb))), где p - полином в log nb |
| Экспоненциальная | O(2nb) |
| Суперэкспоненциальная | O(nbnb) или O(22^(nb)) |
Алгоритм с постоянной, логарифмической и полиномиальной сложностью считают выполнимым для любого размера..Алгоритм с показательной и суперэкспоненциальной сложностью считают неосуществимым, если. nb. очень большое. Алгоритм с субэкспоненциальной сложностью (такой как. O(2p(log(nb))) ) выполним, если nb не является очень большим.
Пример L.9
Как показано в примере L.4, сложность обычного возведения в степень -. f(nb) = 2nb x nb2.. Большая O -нотация для этого алгоритма -. O (2nbx nb2 ), больше, чем показательный. Этот алгоритм неосуществим, если. nb.выбрать. очень большим.
Пример L.10
Как показано в примере L.5, сложность быстрого показательного алгоритма. f (nb) = 2nb3 большая O(nb3) -нотация для этого алгоритма. которая является полиномиальной. Этот алгоритм выполним; он используется в криптографической системе RSА.
Пример L.11
Предположим, что криптографическая система имеет длину ключа nb бит. Чтобы провести атаку грубой силы для этой системы, противник должен проверить 2nb.различных ключа. Это означает, что алгоритм должен пройти 2nb шагов.Если N - число побитных операций для каждого шага, сложность алгоритма должна быть. f(nb) = N x 2nb. Даже если. N - константа, сложность этого алгоритма показательна, O(2nb). Поэтому для большого nb.атака неосуществима. В лекции 6 курса "Математика криптографии и теория шифрования" мы видели, что DES с ключом на 56 битов уязвимы к атаке грубой силы, но для 3DES с ключом 112 бит она неосуществима. В лекции 7 курса "Математика криптографии и теория шифрования" мы также убедились, что AES с ключом на 128 битов имеет иммунитет к этой атаке.
