|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Простые числа
Асимметрично-ключевая криптография, которую мы обсудим в лекциях 14-15, базируется на некоторых положениях теории чисел, включая теории, связанные с простыми числами, разложением на множители составных объектов в простые числа, модульном возведение в степень и логарифмах, квадратичных вычетах и китайской теореме об остатках. Эти проблемы будут рассмотрены здесь, в чтобы упростить понимание лекциии 14-15.
12.1. Простые числа
Асимметрично-ключевая криптография широко использует простые числа. Тема простых чисел — большая часть любой книги по теории чисел. Эта лекция обсуждает только несколько понятий и фактов, чтобы открыть путь к лекциях 14-15.
Определение
Положительные целые числа могут быть разделены на три группы: число 1, простые числа и составные объекты, как это показано на рис. 12.1.
Положительное целое число — простое число тогда и только тогда, когда оно точно делимо без остатка на два целых числа — на 1 и на само себя. Составной объект — положительное целое число больше с чем двумя делителями.
Пример 12.1
Какое наименьшее простое число?
Решение
Наименьшее простое число — 2, оно делится без остатка на 2 (само на себя) и 1. Обратите внимание, что целое число 1 — не простое число согласно определению, потому что простое число должно быть делимо без остатка двумя различными целыми числами, не больше и не меньше. Целое число 1 делимо без остатка только на себя; поэтому 1 — это не простое число.
Пример 12.2
Перечислите простые числа, меньшие, чем 10.
Решение
Есть четыре простых числа меньше чем 10: 2, 3 5 и 7. Интересно, что процент простых чисел в диапазоне 1-10 — 40%. С увеличением диапазона процент уменьшается.
Взаимно простые числа
Два положительных целых числа a и b являются взаимно простыми (coprime), если НОД (a, b) = 1, потому что число 1 является взаимно простым с любым целым числом. Если p — простое число, тогда все числа от 1 до p–1 являются взаимно простыми к p. В "Модульная арифметика" мы обсуждали множество Zn*, чьи элементы — все числа, взаимно простые с n. Множество Z * является тем же самым, за исключением того, что модуль (p) — простое число.
Количество простых чисел
После того как понятие простых чисел было определено, естественно возникает вопрос: число простых чисел конечно или бесконечно? Возьмем число n. Сколько есть простых чисел меньших, чем это число, или равных n?
Число простых чисел
Число простых чисел бесконечно. Приведем нестрогое доказательство: предположим, что множество простых чисел конечно (ограничено), и пусть p — наибольшее простое число. Перемножим все простые числа, входящие в это множество, и получим результат 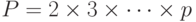 . Целое число (P + 1) не может иметь простого делителя
. Целое число (P + 1) не может иметь простого делителя  (p – наибольшее простое число). Тогда этот делитель должен быть одним из множителей, входящих в P. Это значит, что q делит P. Если q также делит (P + 1), то q делит (P + 1) – P = 1. Единственное число, которое делит 1, — это сама 1, которая не является простым числом. Поэтому q должно быть большим, чем p, и ряд простых чисел не исчерпывается принятым конечным множеством.
(p – наибольшее простое число). Тогда этот делитель должен быть одним из множителей, входящих в P. Это значит, что q делит P. Если q также делит (P + 1), то q делит (P + 1) – P = 1. Единственное число, которое делит 1, — это сама 1, которая не является простым числом. Поэтому q должно быть большим, чем p, и ряд простых чисел не исчерпывается принятым конечным множеством.
Пример 12.3
Как тривиальный пример, предположим, что единственные простые числа находятся в множестве {2, 3, 5, 7, 11, 13, 17}. Здесь P = 510510 и P + 1 = 510511. Однако 510511 состоит из следующих простых чисел  ; ни одно из этих простых чисел не было в первоначальном списке. Эти три простых числа больше, чем 17.
; ни одно из этих простых чисел не было в первоначальном списке. Эти три простых числа больше, чем 17.
Число простых чисел, меньших n
Чтобы рассмотреть вторую возможность, введем функцию  , которая определяет число простых чисел, меньших или равных n. Ниже показаны значения этой функции для различного
, которая определяет число простых чисел, меньших или равных n. Ниже показаны значения этой функции для различного  .
.
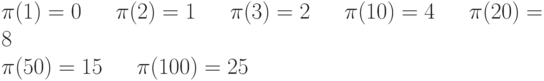
Но если n является очень большим, как мы можем вычислить  ? Для ответа мы можем использовать только приближение, которое показано ниже:
? Для ответа мы можем использовать только приближение, которое показано ниже:
![\left[ {n/(\ln n)} \right] < \pi (n) < [n/(\ln n-1.08366)]](/sites/default/files/tex_cache/83f3eec9dfdd7db56d677af64e67ba61.png)
Гаусс обнаружил верхний предел; Лагранж обнаружил нижний предел.
Пример 12.4
Найдите количество простых чисел, меньших, чем 1 000 000.
Решение
Приближение дает диапазон от 72 383 до 78 543. Фактическое число простых чисел — 78 498.
Проверка на простое число
Следующий вопрос, который приходит на ум: как мы можем определить для данного числа n, является ли оно простым числом? Мы должны проверить, делимо ли без остатка это число всеми простыми числами, меньшими, чем 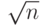 . Мы знаем, что этот метод неэффективен, но он хорош для начала.
. Мы знаем, что этот метод неэффективен, но он хорош для начала.
Пример 12.5
Действительно ли 97 — простое число?
Решение
Наибольшее ближайшее целое число —  . Простые числа меньше чем 9 — 2, 3, 5 и 7. Проверим, делимо ли без остатка 97 любым из этих номеров. Ответ: не делимо, так что 97 — простое число.
. Простые числа меньше чем 9 — 2, 3, 5 и 7. Проверим, делимо ли без остатка 97 любым из этих номеров. Ответ: не делимо, так что 97 — простое число.
Пример 12.6
Действительно ли 301 — простое число?
Решение
Наибольшее ближайшее целое число . Мы должны проверить 2, 3, 5, 7, 11, 13 и 17. Числа 2, 3 и 5 не делят 301, но 7 — делит. Поэтому 301 — не простое число.
. Мы должны проверить 2, 3, 5, 7, 11, 13 и 17. Числа 2, 3 и 5 не делят 301, но 7 — делит. Поэтому 301 — не простое число.
Решето Эратосфена
Греческий математик Эратосфен изобрел метод, как найти все простые числа, меньшие, чем n.
Метод назван решетом Эратосфена. Предположим, что мы хотим найти все числа, меньшие, чем 100. Мы записываем все числа между 2 и 100. Поскольку  , мы должны видеть, делим ли без остатка любой номер меньше чем 100 на числа 2, 3, 5 и 7. Таблица 12.1 показывает результат.
, мы должны видеть, делим ли без остатка любой номер меньше чем 100 на числа 2, 3, 5 и 7. Таблица 12.1 показывает результат.
Процесс состоит в следующем:

