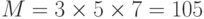НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 12: Простые числа

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Доступ: свободный | Студентов: 3545 / 611 | Оценка: 4.28 / 4.00 | Длительность: 26:16:00

ISBN: 978-5-9963-0242-0

Темы: Безопасность, Математика

Специальности: Математик

|

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

12.4. Китайская теорема об остатках

Китайская теорема об остатках (CRT — Chinese Reminder Theorem) используется, чтобы решить множество уравнений с одной переменной, но различными взаимно простыми модулями, как это показано ниже:

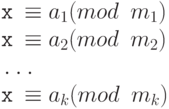
$\tt\parindent0pt x \equiv a_{1} (mod\ m_{1}) x \equiv a_{2} (mod\ m_{2}) … x \equiv a_{k} (mod\ m_{k})$

Китайская теорема об остатках утверждает, что вышеупомянутые уравнения имеют единственное решение, если модули являются взаимно простыми.

Пример 12.35

Следующий пример содержит систему уравнений с различными модулями:

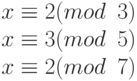
$\tt\parindent0pt $x \equiv 2(mod\ 3)$ $x \equiv 3(mod\ 5)$ $x \equiv 2(mod\ 7)$$

Для этой системы уравнений x = 23. Это значение удовлетворяет все уравнения: $23 \equiv 2\left( {\bmod 3} \right)$ , $23 \equiv 3\left( {\bmod 5} \right)$ , $23 \equiv 2\left( {\bmod 7} \right)$ .

Решение

Решение системы уравнений выполняется в следующем порядке:

Найти $M = {m_1} \times {m_2} \times \ldots \times {m_k}$ . Это общий модуль.
Найти M₁ = M/m₁, M₂ = M/m₂,…., M_k = M/m_k.
Используя соответствующие модули m₁, m₂,…., m_k, найти мультипликативную инверсию M₁, M₂,…, M_k. Обозначим ее M₁^-1, M₂^-1,…, M_k^-1.
Решение системы уравнений

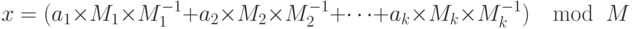
$x = (a_{1} \times M_{1} \times M_{1}^{-1} + a_{2} \times M_{2} \times M_{2}^{-1}+\dots+ a_{k} \times M_{k} \times M_{k}^{-1}) \mod\ M$

Обратите внимание, что система уравнений может иметь решение, даже если модули не взаимно простые. Однако в криптографии мы интересуемся только решением уравнений с взаимно простыми модулями.

Пример 12.36

Найдите решение системы уравнений

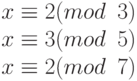
$\tt\parindent0pt $x \equiv 2(mod\ 3)$ $x \equiv 3(mod\ 5)$ $x \equiv 2(mod\ 7)$$

Из предыдущего примера мы уже знаем, что ответ x = 23. Определим его в четыре шага.

Решение

$M = 3 \times 5 \times 7 = 105$
M₁ = 105/3 = 35, M₂ = 105/5 =21, M₃ = 105/7 = 15
Инверсии M₁^-1 = 2, M₂^-1 = 1, M₃^-1 = 1
$x = 2 \times 35 \times 2 + 3 \times 21 \times 1 + 2 \times 15 \times 1 = 23\bmod 105$

Пример 12.37

Найти целое, которое дает в остатке 3, если его разделить на 7 и 13, но без остатка делится на 12.

Решение

Это проблема китайской теоремы об остатке. Мы можем составить три уравнения и найти значение x.

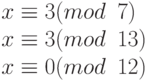
$\tt\parindent0pt $x \equiv 3(mod\ 7)$ $x \equiv 3(mod\ 13)$ $x \equiv 0(mod\ 12)$$

Если проведем четыре шага, мы найдем x = 276. Можем проверить, что 276 = 3 mod 7, 276 = 3 mod 13 и 276 делится на 12 (частное 23 и остаток 0).

Приложения

Китайская теорема об остатках часто применяется в криптографии. Одно из таких применений – решение квадратных уравнений — будет обсуждаться в следующей секции. Другое приложение — представление очень большого числа в виде списка малых целых чисел.

Пример 12.38

Предположим, нам надо вычислить z = x + y, где x = 123 и y = 334, но система принимает только числа меньше 100. Эти числа можно представить следующими уравнениями:

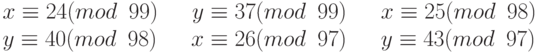
$\tt\parindent0pt $x \equiv 24(mod\ 99) \ \ \ y \equiv 37(mod\ 99)\ \ \ x \equiv 25(mod\ 98)$ $y \equiv 40(mod\ 98)\ \ \ x \equiv 26(mod\ 97) \ \ \ y \equiv 43(mod\ 97)$$

Сложим каждое уравнение x с соответствующим уравнением y:

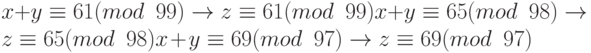
$\tt\parindent0pt $x + y \equiv 61(mod\ 99) \to z \equiv 61(mod\ 99)x + y \equiv 65(mod\ 98) \to$ $z \equiv 65(mod\ 98)x + y \equiv 69(mod\ 97) \to z \equiv 69(mod\ 97)$$

Теперь эти три уравнения могут быть решены, используя китайскую теорему об остатках, чтобы найти z. Один из приемлемых ответов равен z = 457.

Дальше >>

Авторизоваться

Математика криптографии и теория шифрования

Простые числа

12.4. Китайская теорема об остатках

Приложения

Вопросы и ответы