|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгебраические структуры
Следующие лекции посвящены обсуждению современных симметрично-ключевых блочных шифров, которые выполняют операции с n -битовыми словами. Понимание и анализ этих шифров требуют некоторого знания разделов современной алгебры, называемых алгебраическими структурами. В начале этой лекции делается обзор алгебраических структур, а затем показывается, как выполнить сложение или умножение c n -битовыми словами.
Алгебраические структуры
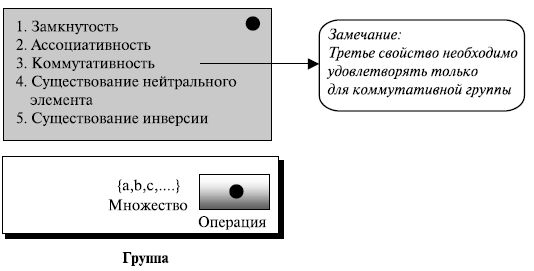
В лекциях 2-3 мы обсуждали некоторые множества чисел, таких как Z, Zn, Zn*, Zp^ и Zp*. Криптография требует, чтобы были заданы множества целых чисел, и операции, определенные для них. Комбинация множеств и операций, которые могут быть применены к элементам множества, называются алгебраической структурой. В этой лекции мы определим три общих алгебраических структуры: группы, кольца и поля ( рис. 5.1).
Группы
Группа ( G ) — набор элементов с бинарной операцией "•" обладает четырьмя свойствами (или удовлетворяет аксиомам), которые будут перечислены ниже.
Коммутативная группа, также называемая абелева, — группа, в которой оператор обладает теми же четырьмя свойствами для групп плюс дополнительным — коммутативностью. Эти пять свойств определены ниже
- Замкнутость. Если a и b — элементы G, то c = a • b — также элемент G. Это означает, что результат применения операции с любыми двумя элементами множества есть элемент этого множества.
- Ассоциативность. Если a, b и c — элементы G, то верно (a• b) • c = a• (b •c) Другими словами, не имеет значения, в каком порядке мы применяем операцию более чем с двумя элементами.
- Коммутативность. Для всех a и b в G мы имеем a • b = b • a. Обратите внимание, что это свойство должно быть верно только для коммутативной группы.
- Существование нейтрального элемента. Для всех элементов в G существует элемент e, который называется нейтральным элементом, такой, что e • a = a • e = a.
- Существование инверсии. Для каждого a в G существует элемент a', называемый инверсией, такой, что a • a' = a' • a = e.
Рисунок 5.2 иллюстрирует понятие группы.
Приложение
Хотя группа включает единственный оператор, свойства, присущие каждой операции, позволяют использование пары операций, если они — инверсии друг друга. Например, если определенный выше оператор — сложение, то группа поддерживает и сложение, и вычитание, ибо вычитание и сложение — аддитивно инверсные операции. Это также верно для умножения и деления. Однако группа может поддержать только сложение/вычитание или умножение/деление, но не оба сочетания операторов одновременно.
Пример 5.1
Множество целых чисел, входящих в вычет с оператором сложения, G = <Zn, +>, является коммутативной группой. Мы можем выполнить сложение и вычитание на элементах этого множества, не выходя за его пределы.
Проверим эти свойства.
- Замкнутость удовлетворяется. Результат сложения двух целых чисел в Zn — другое целое число в Zn.
- Ассоциативность удовлетворяется. Результат 4 + (3 + 2) тот же самый, что в случае (4 + 3) + 2.
- Коммутативность удовлетворяется. Мы имеем 3 + 5 = 5 + 3.
- Нейтральный элемент — 0. Мы имеем 3 + 0 = 0 + 3 = 3.
- Каждый элемент имеет аддитивную инверсию. Инверсия элемента — его дополнение. Например, инверсия 3 — это –3 ( n – 3 в Zn ), и инверсия –3 — это 3. Инверсия позволяет нам выполнять вычитание на множестве.
Пример 5.2
Множество Zn* с оператором умножения G = <Zn*, >, является также абелевой группой. Мы можем выполнить умножение и деление на элементах этого множества, не выходя за его пределы. Это облегчает проверку первых трех свойств. Нейтральный элемент равен 1. Каждый элемент имеет инверсию, которая может быть найдена согласно расширенному алгоритму Евклида.
Пример 5.3
Хотя мы обычно представляем группу как множество чисел с обычными операторами, такими, как сложение или вычитание, определения группы позволяют нам определять любое множество объектов и операций, которые удовлетворяют вышеупомянутым свойствам. Определим множество G = <{a, b, c, d,}, •> и операцию, показанную с помощью таблицы 5.1.
Это — абелева группа. Все пять свойств удовлетворены.
- Замкнутость удовлетворена. Применение оператора на любой паре элементов дает в результате другой элемент этого множества.
- Ассоциативность также удовлетворена. Чтобы доказать это, мы должны проверить свойство для любой комбинации из трех элементов. Например, (a+ b) + c = a+ (b + c) = d.
- Операция коммутативна. Мы имеем a + b = b + a.
- Группа имеет нейтральный элемент, которым является a.
- Каждый элемент имеет инверсию. Обратные пары могут быть найдены. В таблице они указаны теневыми элементами в каждой строке. Пары — (a, a), (b, d), (c, c).
Пример 5.4
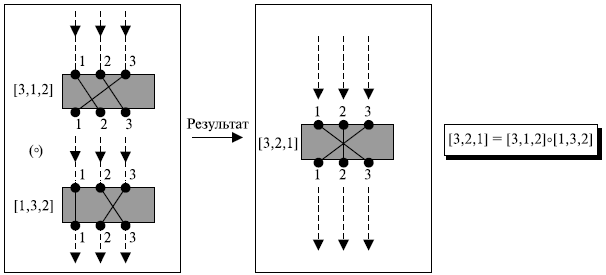
В группе элементы в множестве не обязательно должны быть числами или объектами; они могут быть правилами, отображениями, функциями или действиями. Очень интересная группа — группа подстановок. Множество всех перестановок и оператор является композицией: применения одной перестановки за другой. Рисунок 5.3 показывает композиции двух перестановок, которые перемещают три входных сигнала, чтобы создать три выходных сигнала.
Входные сигналы и выходные сигналы могут быть символами (лекции 2-3) или битами. Мы изобразили каждую перестановку прямоугольником, внутри которого показано, где исходящий входной сигнал и индекс ( 1,2,3 ) определяет выходной сигнал. Композиция состоит из двух перестановок одна за другой. При трех входных сигналах и трех выходных сигналах может быть 3! или 6 различных перестановок. Таблица 5.2 дает определение этого оператора. Первая строка — первая перестановка; первый столбец — вторая перестановка. Результат содержится на пересечении.
В этом случае удовлетворены только четыре свойства; поэтому группа — не абелева.
- Замкнутость удовлетворена.
- Ассоциативность также удовлетворена. Чтобы доказать это, мы должны проверить свойство для любой комбинации из трех элементов.
- Свойство коммутативности не удовлетворено. Это может быть легко проверено, но мы оставим это для упражнения.
- Множество имеет нейтральный элемент [1 2 3] (перестановка отсутствует). Эти элементы показаны другим цветом.
- Каждый элемент имеет инверсию. Обратные пары могут быть найдены, если использовать нейтральные элементы.
Пример 5.5
В предыдущем примере мы показали, что множество перестановок с композицией операций — группа. Поэтому использование двух перестановок (одна за другой) не могут усилить безопасность шифра. Мы сможем всегда найти перестановку, которая может сделать ту же самую операцию, используя свойства замкнутости.
Конечная группа
Группа называется конечной группой, если множество имеет конечное число элементов; иначе это — бесконечная группа.
Порядок группы
Порядок группы, G, — это число элементов в группе. Если группа не конечна, ее порядок бесконечен; если конечна, порядок конечен.
Подгруппы
Подмножество H группы G — подгруппа G, если само H — группа относительно операции на G. Другими словами, если G = <S, •> — группа, то H = <T, •> — группа для той же самой операции, и T — непустое подмножество S, то H — подгруппа G. Вышеупомянутое определение подразумевает, что:
- если a и b — члены обеих групп, то c = a • b — также элемент обеих групп;
- для группы и подгруппы имеется один и тот же нейтральный элемент;
- если этот элемент принадлежит обеим группам, инверсия a — также элемент обеих групп;
- группа, полученная с помощью нейтрального элемента G, H = <{e}, •>, является подгруппой G ;
- каждая группа — подгруппа самой себя.
Пример 5.6
Является ли группа H = <Z10, +> подгруппой группы G = <Z12, +>?
Решение
Ответ — нет. Хотя H — подмножество G, операции, определенные для этих двух групп, различны. Операция H — сложение по модулю 10 ; операция в G — сложение по модулю 12.