НОУ ИНТУИТ | Теория экономических механизмов. Лекция 5: Эффективные и оптимальные механизмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Оптимальные механизмы

Теперь вернемся к более общей ситуации и начнем наши рассуждения с оптимальных механизмов. Чтобы построить оптимальный механизм, нужно для прямого механизма $(\mathbf Q, \mathcal M)$ максимизировать ожидание дохода продавца:

$\mathbf E(R) = \sum\limits_{i=1}^N\mathbf E[m_i(X_i)],$

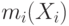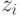где X_i — распределение ценностей агента , а m_i(X_i) — его выплата. Далее мы подсчитаем это ожидание явно, но сначала вспомним обозначения доходности и выплаты агентов. Через q_i(z_i) мы обозначаем ожидаемую доходность агента , когда он говорит z_i , а остальные говорят правду:

$q_i(z_i) = \int_{\mathcal X_{-i}}Q_i(z_i,\mathbf x_{-i})f_{-i}(\mathbf x_{-i})d\mathbf x_{-i}.$

А через m_i(z_i) — ожидаемую выплату агента в той же ситуации:

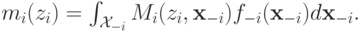
$m_i(z_i) = \int_{\mathcal X_{-i}}M_i(z_i,\mathbf x_{-i})f_{-i}(\mathbf x_{-i})d\mathbf x_{-i}.$

Напомним, что отрицательные индексы означают "все, кроме"; например, 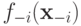$f_{-i}(\mathbf x_{-i})$ означает распределение ценностей всех агентов, кроме агента .

Для вывода ожидаемого дохода продавца будем использовать формулу для ожидаемой выплаты 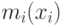m_i(x_i) агента , которую мы получали в теореме об эквивалентности доходности (теорема 4.1):

$\mathbf E[m_i(X_i)] = \int_0^{\omega_i}m_i(x_i)f_i(x_i)dx_i = \\ = m_i(0) + \int_0^{\omega_i}q_i(x_i)x_if_i(x_i)dx_i - \int_0^{\omega_i}\int_0^{x_i}q_i(t_i)f_i(x_i)dt_idx_i.$

Преобразуем двойной интеграл, поменяв в нем порядок интегрирования. Здесь снова никаких теоретических проблем с изменением порядка не возникает; область интегрирования показана на рис. 5.2.

Рис. 5.2. Область интегрирования интеграла

$\int_0^{\omega_i}\int_0^{x_i}q_i(t_i)f_i(x_i)dt_idx_i = \int_0^{\omega_i}\int_{t_i}^{\omega_i}q_i(t_i)f_i(x_i)dx_idt_i = \\ = \int_0^{\omega_i}(1-F_i(t_i))q_i(t_i)dt_i.$

Запишем снова ожидаемую выплату агента и вспомним, что q_i по определению — интеграл по $\mathbf x_{-i}$ . Тогда интегралы по x_i и $\mathbf x_{-i}$ весьма удобно объединятся:

$\mathbf E[m_i(X_i)] = m_i(0) + \int_0^{\omega_i}\left(x_i - \frac{1-F_i(x_i)}{f_i(x_i)}\right)q_i(x_i)f_i(x_i)dx_i = \\ = \int_\mathcal X\left(x_i - \frac{1-F_i(x_i)}{f_i(x_i)}\right)Q_i(\mathbf x)f(\mathbf x)d\mathbf x.$

В итоге, просуммировав по всем агентам, получаем ожидаемый доход продавца:

$\mathbf E[R] = \sum_{i=1}^N\mathbf E[m_i(X_i)] =\sum_{i=1}^Nm_i(0)+\sum_{i=1}^N\int_{\mathcal X}\left(x_i - \frac{1-F_i(x_i)}{f_i(x_i)}\right)Q_i(\mathbf x)f(\mathbf x)d\mathbf x.$

Осталось максимизировать это выражение при следующих условиях:

правдивость, что равносильно неубыванию ;
рациональность, что равносильно $m_i(0)\le 0$ , то есть если у агента собственная ценность , то он должен заплатить не больше , чтобы не быть в убытке.

Все эти равносильности уже объяснялись в лекции "Теорема об эквивалентности доходности" .

Введем для упрощения записи понятие виртуальной ценности предмета для агента :

$\psi_i(x_i)=x_i - \frac{1-F_i(x_i)}{f_i(x_i)}.$

Смысл виртуальной ценности в том, что продавец должен максимизировать 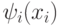$\psi_i(x_i)$ , если хочет быть оптимальным. Заметим, что если максимизировать x_i , то он будет эффективным — вот и вся разница между эффективностью и оптимальностью.

Докажем, что $\mathbf E[\psi_i(X_i)] = 0$ :

$\mathbf E[\psi_i(X_i)]=\mathbf E(X_i)-\int_{X_i} \frac{1-F_i(x_i)}{f_i(x_i)}f(x_i)dx_i=\mathbf E(X_i)-\int_{X_i}\left(1-F_i(x_i)\right)dx_i.$

Рассмотрим теперь отдельно интеграл справа. Поменяем порядок интегрирования, как уже было сделано в показанном на рис. 5.2 случае:

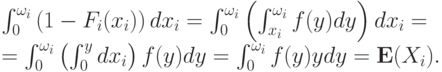
$\int_0^{\omega_i}\left(1-F_i(x_i)\right)dx_i = \int_0^{\omega_i}\left(\int_{x_i}^{\omega_i} f(y)dy\right)dx_i = \\ = \int_0^{\omega_i}\left(\int_0^y dx_i\right)f(y)dy = \int_0^{\omega_i} f(y)ydy = \mathbf E(X_i).$

Таким образом мы получили, что математическое ожидание виртуальной ценности каждого агента равно нулю.

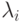Будем называть задачу дизайна механизмов регулярной, если $\psi_i$ является возрастающей функцией от x_i для любого . Это эквивалентно тому, что функция риска $\lambda_i$ возрастает, так как

$\psi_i(x_i) = x_i - \frac1{\lambda_i(x_i)}.$

В дальнейшем мы будем рассматривать только регулярные задачи.

Запишем ожидаемый доход продавца в терминах виртуальных ценностей:

$\mathbf E[R]=\sum_{i=1}^Nm_i(0)+\sum_{i=1}^N\int_{\mathcal X}\psi_i(x_i)Q_i(\mathbf x)f(\mathbf x)d\mathbf x.$

Рассмотрим подынтегральное выражение 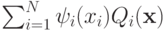$\sum_{i=1}^N\psi_i(x_i)Q_i(\mathbf x)$ . $\mathbf Q$ похожа на весовую функцию, взвешивающую $\psi_i$ . Резонно было бы дать максимальный вес максимальному $\psi_i$ (если он положительный), а про остальные забыть. Это максимизировало бы функцию в каждой точке, а значит, и интеграл тоже. Это и будет идеей конструкции, но нам еще придется учесть ограничения (правдивость и рациональность).

Итак, рассмотрим прямой механизм $(\mathbf Q, \mathcal M)$ , у которого выполняются следующие свойства:

Функция распределения $\mathbf Q$ распределяет объект покупателю с положительной вероятностью тогда и только тогда, когда у него максимальная и неотрицательная виртуальная ценность:
$Q_i(\mathbf x)>0\quad \Leftrightarrow\quad \psi_i(x_i)=\max_{j=1..N}\psi_j(x_j)\ge 0$ .

Если покупателей с максимальным 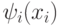$\psi_i(x_i)$ несколько, то на них может быть любое положительное распределение $\mathbf Q$ , то есть просто не важно, кому именно из них достанется объект.
Плата 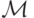$\mathcal M$ определяется следующим образом:
$M_i(\mathbf x)=Q_i(\mathbf x)x_i - \int_0^{x_i}Q_i(z_i,\mathbf x_{-i})dz_i$ .

Такая функция платы нужна для того, чтобы выполнялось условия рациональности.

Оказывается, что (при условии регулярности) это и есть оптимальный механизм.

Теорема 5.1. Для регулярной задачи дизайна механизмов механизм 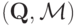$(\mathbf Q,\mathcal M)$ , где

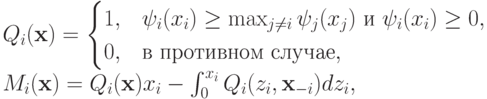
$Q_i(\mathbf x)&=&\begin{cases} 1, & \psi_i(x_i)\ge\max_{j\neq i}\psi_j(x_j)\text{ и }\psi_i(x_i)\ge 0,\\ 0, & \text{в противном случае},\end{cases} \\ M_i(\mathbf x)&=&Q_i(\mathbf x)x_i - \int_0^{x_i}Q_i(z_i,\mathbf x_{-i})dz_i,$

является правдивым, рациональным и оптимальным среди всех рациональных^{3Конечно, если разрешить аукционеру принудительно собирать любую сумму с агентов-участников, можно получить доход и побольше. Но мы все же предполагаем, что находимся на свободном рынке, и агенты вольны выбирать, участвовать им в аукционе или нет. Следовательно, нас интересуют только рациональные аукционы — остальные просто останутся без участников.}.

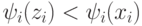Доказательство. Во-первых, покажем правдивость построенного нами механизма. Пусть z_i<x_i . Тогда, по регулярности, $\psi_i(z_i)<\psi_i(x_i)$ , и, значит,

$\forall\mathbf x_{-i}\quad Q_i(z_i,\mathbf x_{-i})\le Q_i(x_i,\mathbf x_{-i}).$

Значит, q_i неубывающая, то есть механизм правдивый.

Во-вторых, покажем рациональность. Очевидно, что

$M_i(0,\mathbf x_{-i})=0.$

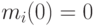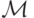Значит, m_i(0)=0 , и механизм рациональный. Заметим, что форма платы $\mathcal M$ в данном случае полностью задана распределением $\mathbf Q$ ; $\mathcal M$ определена с точностью до константы, которую мы изначально приняли такой, чтобы выполнялось m_i(0)=0 .

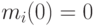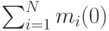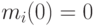Таким образом, это рациональный и правдивый механизм. Кроме того, он оптимален, так как максимизирует каждое из двух слагаемых формулы дохода продавца по отдельности. Во-первых, он максимизирует $\sum_{i=1}^Nm_i(0)$ , потому что $m_i(0)\le 0$ для всех рациональных механизмов, а в нашем m_i(0)=0 . Во-вторых, он максимизирует 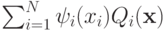$\sum_{i=1}^N\psi_i(x_i)Q_i(\mathbf x)$ в каждой точке, потому что дает весь имеющийся вес 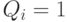Q_i=1 агенту с максимальной виртуальной ценностью 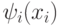$\psi_i(x_i)$ . Значит, он максимизирует и

$\mathbf E[R]=\sum\limits_{i=1}^Nm_i(0)+\sum\limits_{i=1}^N\int_{\mathcal X}\psi_i(x_i)Q_i(\mathbf x)f(\mathbf x)d\mathbf x$

Давайте теперь изучим то, что у нас получилось. Максимальный доход нашего оптимального аукциона получается по простой формуле:

$\max\mathbf E[R] = \mathbf E\left[\vphantom{1^2}\max\{\psi_1(X_1),\ldots,\psi_N(X_N),0\}\right].$

Ноль добавляется на случай, если все виртуальные ценности окажутся отрицательными.

Проанализируем теперь, сколько придется заплатить победителю такого аукциона. Рассмотрим новые функции

$y_i(\mathbf x_{-i}) = \inf\{z_i\mid \psi_i(z_i)>0\ \text{и}\ \forall j\neq i\ \psi_i(z_i)\ge \psi_j(x_j)\}.$

Это минимальное значение ставки игрока , которое позволит ему выиграть аукцион (даст ему положительную виртуальную ценность, которая окажется больше, чем виртуальные ценности всех других участников). Тогда определение правила распределения $\mathbf Q$ можно переписать как

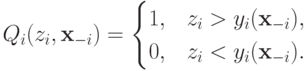
$Q_i(z_i,\mathbf x_{-i})=\begin{cases} 1, & z_i>y_i(\mathbf x_{-i}),\\ 0, & z_i<y_i(\mathbf x_{-i}).\end{cases}$

Подсчитаем интеграл:

$\int_0^{x_i}Q_i(z_i,\mathbf x_{-i})dz_i = \begin{cases} x_i-y_i(\mathbf x_{-i}), & x_i>y_i(\mathbf x_{-i}),\\ 0, & x_i<y_i(\mathbf x_{-i}).\end{cases}$

Значит, правило выплаты 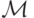$\mathcal M$ можно с использованием функций y_i переписать как

$M_i(\mathbf x) = \begin{cases} y_i(\mathbf x_{-i}), & x_i>y_i(\mathbf x_{-i}),\\ 0, & x_i<y_i(\mathbf x_{-i}).\end{cases}$

Иначе говоря, только победитель что-то платит, и он платит минимальную ставку $y_i(\mathbf x_{-i})$ , достаточную, чтобы обеспечить ему выигрыш. Но это в точности основной принцип аукциона второй цены! Значит, выше мы доказали, что оптимальный аукцион при продаже одной вещи нейтральным к риску агентам — это аукцион Викри с резервной ценой. Более того, из теоремы 5.1 можно извлечь и оптимальную резервную цену.

Рассмотрим для простоты симметричный случай: пусть все агенты симметричны, то есть плотности распределения ценностей 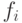f_i равны. Тогда все виртуальные ценности $\psi_i=\psi$ . Тогда получаем, что

$y_i(\mathbf x_{-i}) = \max\left\{\max\limits_{j\neq i}x_j, \psi^{-1}(0)\right\}.$

Таким образом, победитель платит максимум из всех остальных ставок или резервную цену, если все остальные ставки меньше. Проще говоря, мы получили в точности аукцион второй цены с резервной ценой

$r = \psi^{-1}(0).$

Пример 5.3. Подсчитаем $\psi^{-1}(0)$ для равномерных распределений на [0,1] . Поскольку

$\psi(x) = x - \frac1{\lambda(x)},$

то $\psi^{-1}(0)$ является корнем уравнения

$x=\frac1{\lambda(x)}.$

Решим это уравнение, используя определение функции риска:

$x=\frac1{\lambda(x)}=\frac{1-F(x)}{f(x)}.$

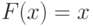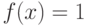Поскольку ценности распределены на [0,1] , то F(x)=x , f(x)=1 . Тогда получаем, что $\psi^{-1}(0)=\frac{1}{2}$ . Иначе говоря, продавцу будет выгодно установить резервную цену в $\frac{1}{2}$ . Здесь мы, конечно, предполагали, что упоминавшийся в предыдущем параграфе доход продавца от удержания вещи у себя (величина x_0 ) равен нулю.

Конец примера 5.3.

Дальше >>

Авторизоваться

Теория экономических механизмов

Эффективные и оптимальные механизмы

Оптимальные механизмы

Вопросы и ответы