Эффективные и оптимальные механизмы
Введение
К примеру, в парадоксе Браесса, который мы рассматривали в лекции "Введение в дизайн механизмов" , "хорошесть" можно было признать самоочевидной: каждому водителю хочется доехать до цели побыстрее, и это совершенно естественным образом совпадает с чаяниями организаторов траспортной развязки — максимально увеличить общую пропускную способность конструкции1Может показаться, что водитель хочет побыстрее проехать сам, а организаторы хотят уменьшить среднее время проезда, и здесь кроется конфликт. На самом деле, конечно, конфликта нет, потому что в любом равновесии все водители проходят маршрут за одно и то же время.
Но что такое "хороший аукцион"? С одной стороны, "хороший" аукцион должен наиболее эффективно распорядиться лотами, на него выставленными: хотелось бы, чтобы вещь досталась тому, кому она действительно более всех нужна. С другой стороны, аукционера тоже забывать не следует: в конце концов, именно он устраивает аукцион так, как ему удобнее, и вполне возможно, что он захочет максимизировать свою прибыль, а вовсе не эфемерное "всеобщее счастье" (это понятие мы чуть ниже конкретизируем).
В этой лекции мы будем рассматривать прямые механизмы, в которых у каждого агента просто спрашивают его тип. Более того, интуиция этой главы полностью ограничивается ситуацией аукциона, в котором продают одну вещь (один лот аукциона). Множество типов агента в такой постановке — это просто множество ![[0,\omega_i]](/sites/default/files/tex_cache/e79e6abfa98bc91dea83f839f5db77e1.png) возможных ценностей, которые агент может приписать продаваемой вещи. Ценность агента
возможных ценностей, которые агент может приписать продаваемой вещи. Ценность агента  , взятая (предположим) по распределению
, взятая (предположим) по распределению  , остается скрытой, известной только ему. При начале аукциона агент подает некоторую ставку
, остается скрытой, известной только ему. При начале аукциона агент подает некоторую ставку 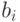 ; в прямом механизме у агента спрашивают его тип, но агент не обязан сообщать свою истинную ценность — если ему это выгодно, он может соврать. А в результате аукциона один из агентов приобретет желаемую вещь и тем самым получит свою внутреннюю ценность
; в прямом механизме у агента спрашивают его тип, но агент не обязан сообщать свою истинную ценность — если ему это выгодно, он может соврать. А в результате аукциона один из агентов приобретет желаемую вещь и тем самым получит свою внутреннюю ценность  , заплатив за это, конечно, некоторую цену.
, заплатив за это, конечно, некоторую цену.
Прямой механизм реализует эту идеологию. Он полностью описывается двумя параметрами: правилом распределения  и правилом выплаты
и правилом выплаты 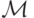 . В случае аукциона с одной вещью
. В случае аукциона с одной вещью 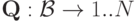 , а
, а  , где
, где  — множество возможных векторов ставок агентов. Иначе говоря, правило
— множество возможных векторов ставок агентов. Иначе говоря, правило  определяет, какой из
определяет, какой из  агентов получит продаваемую вещь, а правило
агентов получит продаваемую вещь, а правило 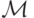 определяет, сколько каждый агент при этом заплатит аукционеру (
определяет, сколько каждый агент при этом заплатит аукционеру (  , кстати говоря, вполне может быть и отрицательным).
, кстати говоря, вполне может быть и отрицательным).
Теперь можно определить два понятия "хорошего аукциона", на которые мы уже намекали выше. Эффективный аукцион хорош для агентов — для участников аукциона.
Определение 5.1. Правило распределения 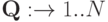 называется эффективным, если оно при эгоистичных действиях агентов максимизирует общественное благосостояние (social welfare) — суммарную внутреннюю полезность всех агентов:
называется эффективным, если оно при эгоистичных действиях агентов максимизирует общественное благосостояние (social welfare) — суммарную внутреннюю полезность всех агентов:

Прямой механизм 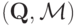 называется эффективным, если у него эффективное правило распределения.
называется эффективным, если у него эффективное правило распределения.
Отметим, что свойство эффективности имеет отношение только к  . Правило выплаты на эффективность вообще не влияет. В простейшем случае аукциона с одним лотом механизм эффективен, если объект достается тому, кому он действительно больше всего нужен, то есть тому агенту, у которого внутренняя ценность
. Правило выплаты на эффективность вообще не влияет. В простейшем случае аукциона с одним лотом механизм эффективен, если объект достается тому, кому он действительно больше всего нужен, то есть тому агенту, у которого внутренняя ценность  максимальна.
максимальна.
А вот оптимальный механизм, в отличие от эффективного, хорош не для покупателей, а для продавца.
Определение 5.2. Будем называть оптимальным механизм, который при эгоистичных действиях агентов максимизирует математическое ожидание дохода продавца 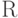 2От слова revenue.:
2От слова revenue.:
![\mathbf E(R) = \sum\limits_{i=1}^N\mathbf E[m_i(X_i)],](/sites/default/files/tex_cache/d58eb7c298595c01862574d00e8a7e99.png)
где 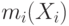 — выплата агента
— выплата агента  ,
,  — его распределение ценностей, а
— его распределение ценностей, а  — конкретное значение ценности агента.
— конкретное значение ценности агента.
Математическое ожидание здесь берется исключительно по возможным типам агентов  , ведь дальнейший ход аукциона строго предопределен: каждый агент рассчитает наиболее выгодную для себя ставку
, ведь дальнейший ход аукциона строго предопределен: каждый агент рассчитает наиболее выгодную для себя ставку 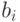 , правило распределения получит все эти ставки и выдаст вещь одному из агентов, правило выплат по тем же ставкам рассчитает выплаты.
, правило распределения получит все эти ставки и выдаст вещь одному из агентов, правило выплат по тем же ставкам рассчитает выплаты.
Аукцион второй цены с резервной ценой
Начнем наше повествование с примера, который призван убедить читателя в том, что эффективные и оптимальные аукционы не всегда тривиальны и не всегда совпадают друг с другом.
Рассмотрим аукцион второй цены (он же аукцион Викри). Напомним, что в этом аукционе победитель платит вторую по величине ставку. Простое рассуждение в теореме 2.1 уже убедило нас, что аукцион второй цены правдив: агентам в нем невыгодно врать. Следовательно, аукцион второй цены эффективен в смысле определения 5.1: так как каждый агент сообщает свою истинную внутреннюю ценность, и аукцион распределяет вещь агенту с наивысшей ставкой, то, следовательно, вещь достанется агенту с наивысшей внутренней ценностью: 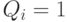 тогда и только тогда, когда
тогда и только тогда, когда  . А это и означает, что
. А это и означает, что 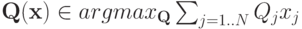 , ведь вещь всего одна.
, ведь вещь всего одна.
Сделаем теперь одну модификацию в нашем (уже эффективном) аукционе: добавим в него резервную цену  . Резервная цена - это такая сумма, что:
. Резервная цена - это такая сумма, что:
- выигравший агент платит максимум между второй ставкой и
 , то есть выплата победителя не может быть меньше
, то есть выплата победителя не может быть меньше  ;
; - если все ставки окажутся ниже
 , продавец оставит товар себе.
, продавец оставит товар себе.
Иначе говоря, резервная цена — минимальная, по которой продавец согласен расстаться с товаром. Поэтому агенты, внутренние ценности которых меньше  , могут просто не участвовать в аукционе — у них все равно нет ни малейшего шанса получить от него доход. А по выплатам данный аукцион будет отличаться от аукциона Викри только в том случае, когда ровно один агент объявит ставку выше резервной цены; если таковых будет хотя бы двое, победитель просто заплатит вторую цену.
, могут просто не участвовать в аукционе — у них все равно нет ни малейшего шанса получить от него доход. А по выплатам данный аукцион будет отличаться от аукциона Викри только в том случае, когда ровно один агент объявит ставку выше резервной цены; если таковых будет хотя бы двое, победитель просто заплатит вторую цену.
Исследуем теперь вопрос о том, каковы будут стратегии и, как следствие, выплаты агентов в новом модифицированном аукционе по сравнению с обычным аукционом Викри.
Во-первых, стратегии не изменятся — по-прежнему доминантная стратегия в том, чтобы говорить правду (напомним, что доминантная стратегия — это такая стратегия, которая выгоднее любой другой вне зависимости от стратегий других агентов). По-прежнему, если агент делает ставку большую, чем его внутренняя ценность, то может случиться так, что ему придется заплатить больше его внутренней ценности, потерпев тем самым убыток. А если он ставит меньше, чем его настоящая цена, то он может не получить объект, несмотря на то, что при правдивой ставке мог заплатить меньше настоящей цены. Рассуждения теоремы 2.1 останутся справедливыми практически без изменений. Таким образом, наличие резервной цены никак не повлияет на то, что аукцион будет правдивым.
Однако изменятся выплаты агентов. В аукционе Викри ожидаемая выплата агента составляла
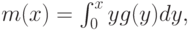
где 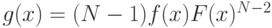 — плотность второй порядковой статистики. Проще говоря, ожидаемая выплата в аукционе второй цены составляет (что вполне логично) ожидание второй сверху ставки.
— плотность второй порядковой статистики. Проще говоря, ожидаемая выплата в аукционе второй цены составляет (что вполне логично) ожидание второй сверху ставки.
Теперь рассмотрим выплату агента в аукционе с резервной ценой. Он, который ставит ровно  , ожидает заплатить просто
, ожидает заплатить просто 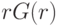 , поскольку вероятность того, что агент выиграет, заплатив
, поскольку вероятность того, что агент выиграет, заплатив  , составляет
, составляет 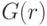 (функция распределения второй порядковой статистики, первообразная
(функция распределения второй порядковой статистики, первообразная 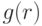 ). Если же агент ставит больше
). Если же агент ставит больше  , то он ожидает заплатить
, то он ожидает заплатить
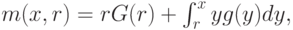
то есть столько же, сколько в первом случае, плюс еще ожидание доплаты за выигрыш благодаря более высокой ставке.
Проверим теперь, что принцип эквивалентности доходности работает и с резервной ценой. В аукционе первой цены анализ будет точно таким же, как раньше, только теперь участник с ценностью  вообще не будет участвовать, и оптимальная ставка агента станет равной
вообще не будет участвовать, и оптимальная ставка агента станет равной
![\beta(x)=\mathbf E[\max\{Y_1,r\}|Y_1<x].](/sites/default/files/tex_cache/e5e98be80dfe9588774022d36e24c449.png)
Раньше это было просто ожидание 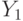 , а теперь стал максимум из
, а теперь стал максимум из 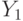 и
и  , поскольку ставка не может быть меньше
, поскольку ставка не может быть меньше  . Получаем, что
. Получаем, что
![\beta(x)=\mathbf E[\max\{Y_1,r\}|Y_1<x] = r\frac{G(r)}{G(x)}+\frac1{G(x)}\int_r^xyg(y)dy.](/sites/default/files/tex_cache/d49c74b7827b3ef7632bd1d3142b2e08.png)
Здесь первое слагаемое относится к случаю, когда  , а второе — к случаю, когда
, а второе — к случаю, когда 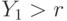 . Так как
. Так как 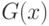 — вероятность того, что
— вероятность того, что 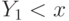 , то ожидаемая выплата агента составит
, то ожидаемая выплата агента составит  . Умножая выражение справа на
. Умножая выражение справа на 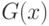 , получим ту же самую выплату для агента
, получим ту же самую выплату для агента  , что и в аукционе второй цены:
, что и в аукционе второй цены:
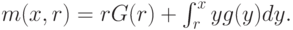
Итак, доходность у аукционов первой и второй цены одинаковая. Найдем ожидаемую доходность продавца от одного агента:
![\mathbf E[m(X,r)] = \int_r^{\omega} m(x,r)f(x)dx =...](/sites/default/files/tex_cache/3d5280f90ba1a534d0ba0b9320f98d0e.png)
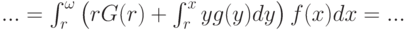
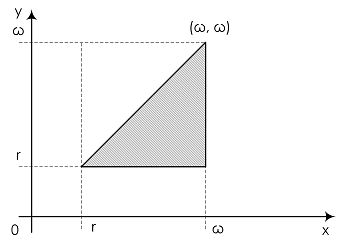
Во втором из этих интегралов, 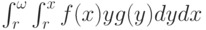 , нам нужно изменить порядок интегрирования. Напомним, что это можно делать без каких-либо проблем и дополнительных условий, если подынтегральная функция ограничена, а область интегрирования компактна. В нашем случае все условия очевидно выполнены, и остается только рассмотреть, по какой именно области мы интегрируем; она изображена на рис. 5.1.
, нам нужно изменить порядок интегрирования. Напомним, что это можно делать без каких-либо проблем и дополнительных условий, если подынтегральная функция ограничена, а область интегрирования компактна. В нашем случае все условия очевидно выполнены, и остается только рассмотреть, по какой именно области мы интегрируем; она изображена на рис. 5.1.
В итоге получается
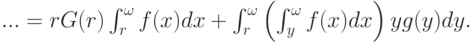
Суммарно мы получили формулу
![\begin{equation}\label{eq3:respay}
\mathbf E[m(X,r)] = rG(r)(1-F(r)) + \int_r^\omega y(1-F(y))g(y)dy.
\end{equation}](/sites/default/files/tex_cache/09f0a7ed4056b37c7200874ede6ecbce.png) |
( 5.1) |
Ранее мы уже доказывали, что аукцион с резервной ценой будет эффективным. Теперь давайте попробуем, не меняя его вид, сделать его настолько оптимальным, насколько это возможно: максимизируем доходность продавца. Обозначим через  его собственную внутреннюю ценность объекта (сумму, в которую он оценивает тот факт, что объект останется у него). Заметим, что раньше мы все время рассматривали частный случай при
его собственную внутреннюю ценность объекта (сумму, в которую он оценивает тот факт, что объект останется у него). Заметим, что раньше мы все время рассматривали частный случай при 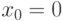 . Тогда общий доход продавца от установки резервной цены
. Тогда общий доход продавца от установки резервной цены  вычисляется как
вычисляется как
![\Pi_0 = N\mathbf E[m(X,r)] + F(r)^Nx_0,](/sites/default/files/tex_cache/72fcc07b49fc7e327a16f1eebce8e1f4.png)
где первое слагаемое нам уже знакомо, а второе относится к случаю, когда никто не получит объект, то есть все  ставок меньше
ставок меньше  .
.
Чтобы максимизировать, продифференцируем по  , подставив вместо
, подставив вместо ![\mathbf E[m(X,r)]](/sites/default/files/tex_cache/72afd2d6ac62a3eb2c9ec701b81423f2.png) выражение (5.1) и не забывая, что
выражение (5.1) и не забывая, что  :
:
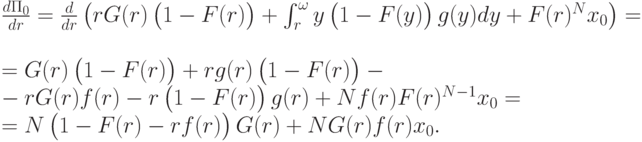
Введем (точнее, вспомним из статистики) новое обозначение — так называемую функцию риска. Эта часто встречающаяся в статистике функция показывает, грубо говоря, мгновенную вероятность "выжить", если считать  распределением вероятности "смерти":
распределением вероятности "смерти":

Пример 5.1. Рассмотрим ситуацию, которая очень часто возникает в медицинской статистике. Предположим, что у нас есть некая выборка людей, которые либо выжили, либо умерли после того или иного заболевания или лечения. Для каждого человека дано время его жизни после начала заболевания. Как описать получающееся распределение вероятностей?
Введем функцию, которая показывает вероятность человека выжить после времени  (буква
(буква  — от слова "survival"):
— от слова "survival"):
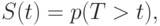
где  — случайная величина, показывающая время до смерти. Соответственно,
— случайная величина, показывающая время до смерти. Соответственно,

где  — функция распределения величины
— функция распределения величины  . А функция риска тогда показывает, какова плотность вероятности умереть в данный момент времени:
. А функция риска тогда показывает, какова плотность вероятности умереть в данный момент времени:
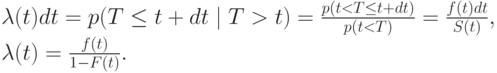
Конец примера 5.1.
Тогда в терминах функции риска производная общего дохода продавца выражается как
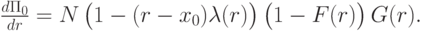
При  производная
производная
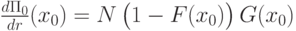
положительна, то есть продавцу выгодно установить резервную цену  . Производная обнуляется только в точке
. Производная обнуляется только в точке 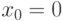 , но при этом тоже выгодно установить резервную цену
, но при этом тоже выгодно установить резервную цену  , что подтвердится в примере ниже. Иначе говоря, резервная цена должна быть выше ценности продукта для продавца.
, что подтвердится в примере ниже. Иначе говоря, резервная цена должна быть выше ценности продукта для продавца.
А максимум доходности продавца получится, если

Пример 5.2. Подсчитаем оптимальную резервную цену для равномерного распределения ценностей агентов на ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Найдем ожидаемый доход у продавца в общем случае и в случае аукциона без резервной цены. Во-первых, поскольку ценности равномерно распределены на
. Найдем ожидаемый доход у продавца в общем случае и в случае аукциона без резервной цены. Во-первых, поскольку ценности равномерно распределены на ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
,

Это значит, что

Подсчитаем оптимальную резервную цену 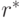 :
:

Пусть 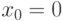 , тогда
, тогда 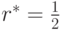 — искомая резервная цена.
— искомая резервная цена.
Найдем теперь ожидаемый доход продавца:
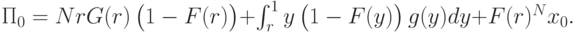
Зная, что 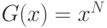 , а значит,
, а значит, 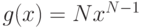 , после упрощения получаем
, после упрощения получаем
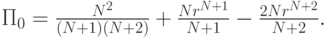
Следовательно, ожидаемый доход продавца без резервной цены (в случае 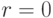 ) равен первому слагаемому
) равен первому слагаемому 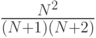 . А при росте резервной цены ожидаемые доходы понемногу растут, достигая максимума при
. А при росте резервной цены ожидаемые доходы понемногу растут, достигая максимума при 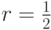 .
.
Конец примера 5.2.
Последнее замечание, которое хочется высказать в этом параграфе, заключается в том, что вместо резервной цены аукционер может с совершенно тем же эффектом ввести плату за участие. Резервная цена  отсекает участников с ценностями
отсекает участников с ценностями  . То же самое получится, если заставить каждого агента заплатить "за вход"
. То же самое получится, если заставить каждого агента заплатить "за вход"

то есть заплатить ожидаемый доход участника с ценностью ровно  , а затем разыграть между ними обычный аукцион Викри, без всяких резервных цен.
, а затем разыграть между ними обычный аукцион Викри, без всяких резервных цен.
Здесь, правда, нужно оговориться, что резервная цена и плата за вход эквивалентны так, как указано выше, только в одном важном предположении: о том, что участвующие в аукционе агенты нейтральны к риску (см. лекцию "Теорема об эквивалентности доходности" ). Если же агенты осторожны(risk-averse), не любят риск, как часто бывает на практике, то плата за участие окажется для них более серьезным барьером, чем резервная цена, и тогда эквивалентность нарушится в сторону уменьшения платы за вход [35].

 :
: