Программирование, основанное на правилах преобразований
Цель лекции: познакомиться с принципами реализации стиля программирования, основанного на правилах преобразований, в языке программирования Mathematica
10.0. Введение
Как справедливо отмечает Е. М. Воробьёв [1, с. 140], понятие преобразования является одним из ключевых в математике. Большинство математических операций, математических объектов, так или иначе, связано с преобразованиями. Так таблицу умножения можно рассматривать как совокупность правил преобразований: согласно им мы с полным правом, не боясь условий и ограничений, можем заменить одно выражение, скажем, 3x3, другим — 9. Математические тождества также представляют собой правила преобразования: например, тождество 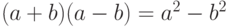 позволяет в математических расчётах заменить его правую часть левой или наоборот.
позволяет в математических расчётах заменить его правую часть левой или наоборот.
Операции математического анализа также не являются исключением. Основной задачей математического анализа является приведение выражений, содержащих суммы, интегралы, производные и т.д., к виду, в котором мы можем заменить их другими выражениями согласно справочным данным. Например, в процессе вычисления мы можем неопределённый интеграл от выражения  по
по  заменить выражением
заменить выражением  . Таким образом, объекты математического анализа также подчиняются правилам преобразования.
. Таким образом, объекты математического анализа также подчиняются правилам преобразования.
Помимо традиционных математических правил преобразования Mathematica имеет широкий набор средств для создания собственных правил. Именно на них и основывается рассматриваемый в настоящей лекции стиль программирования.
Программирование, основанное на правилах преобразования (rule-based programming), характеризуется преобразованием объектов данных различных типов (М. А. Марин и др. [10]). Преобразования есть суть вычисления; они описываются правилами замены одних объектов другими согласно некоторому шаблону. Программирование, основанное на правилах преобразования, является наиболее естественным для высокоорганизованного языка программирования Mathematica. Для ознакомления с данным стилем программирования воспользуемся логикой изложения, применённой в работе Е. М. Воробьёва [1].
10.1. Правила преобразования
10.1.1. Глобальные правила преобразования
Е. М. Воробьёв [1, с. 141] начинает знакомство читателей с правилами преобразований с уже известного нам простейшего правила — присвоения некоторого значения a символу x. С инфиксной формой немедленного присваивания мы познакомились в лекции 2 настоящего курса и знаем, что оно осуществляется при помощи знака " = ". Таким образом, выражение x=a означает, что во всех выражениях в тексте программы, содержащих x, его следует заменить выражением a. Поскольку замена осуществляется во всех выражениях программы, то правило преобразования, задаваемое немедленным присваиванием, является глобальным. Внутренней формой операции немедленного присваивания является функция Set[expr1,expr2]: она заменяет выражение expr1 выражением expr2. Е. М. Воробьёв [1, с. 141] так описывает процесс присваивания: "Выражение Set[expr1,expr2] вычисляется следующим образом. Аргумент expr1 вовсе не вычисляется, выражение expr2 вычисляется, и это вычисленное значение присваивается выражению expr1". Он также отмечает, что такой порядок выполнения функции не случаен и имеет строгое обоснование. Рассмотрим это утверждение на примере. Пусть мы задали выражение y=10, то есть, символу y присвоили значение 10. Затем нам понадобилось присвоить символу y новое значение, например, 5, для чего мы задали функцию Set[y,5]. Если бы при выполнении этой функции первый аргумент (y в нашем случае) вычислялся, то Mathematica бы решила, что мы хотим присвоить значение 5 числу 10, что граничит с разумным. Подобного парадокса и помогает избежать описанный алгоритм вычисления функции Set.
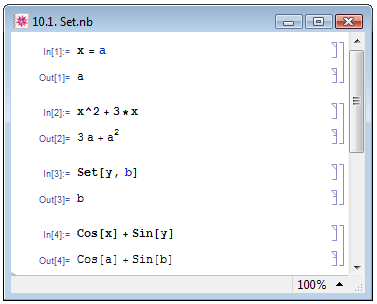
Примеры задания и использования глобального правила преобразования при помощи функции немедленного присваивания Set в инфиксной (In[1] и In[2]) и внутренней (In[3] и In[4]) форме см. на рис. 10.1.
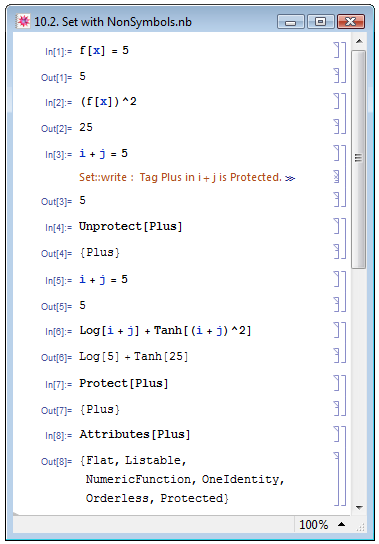
В примерах на рис. 10.1 мы присваивали выражения некоторым символам, хотя, в принципе в качестве выражения expr1, которому присваивается значение expr2, может выступать любое выражение. В примере In[1] на рис. 10.2 мы присвоили некоторой неопределённой функции f[x] значение 5, а в примере In[2] вычислили квадрат выражения f[x]: результат вычисления в Out[2] непосредственно связан с ранее присвоенным выражению численным значением 5.
Однако если мы попытаемся присвоить значение выражению, содержащему в теле некоторую встроенную функцию, например, Plus (пример In[3] на рис. 10.2), то нас постигнет неудача: значение не будет присвоено и Mathematica выдаст предупреждающее сообщение о том, что функция Plus обладает атрибутом Protected. Этот атрибут защищает выражение с данным заголовком от присваивания значений. И всё же даже выражениям с защищёнными заголовками значения могут быть присвоены. Для этого следует убрать из списка принадлежащих функции атрибутов атрибут Protected, применив к ней функцию Unprotect (пример In[4]). После этой процедуры никаких препятствий к присвоению значений не остаётся (примеры In[5] и In[6]). Похожую процедуру для функции Power описывает Е. М. Воробьёв [1, с. 144–145].
Однако Mathematica приписывает функциям атрибут Protected не из желания усложнить пользователю жизнь. Дело в том, что в процессе вычислений программе приходится иметь дело с большим числом правил преобразований. Поскольку большинство встроенных функций, таких, как Plus, Times, Power и др., используются при вычислении достаточно часто, то любое дополнительное правило преобразования, ассоциированное с ними, оказывает влияние на скорость вычислений и может значительно замедлить работу программы. Именно поэтому следует снова защитить такие функции от присваивания, если атрибут Protected однажды был убран из списка их атрибутов. Делается это, как не сложно предположить, при помощи функции Protect. Так в примере In[7] мы снова присваиваем функции Plus атрибут Protected, а в In[8] убеждаемся в том, что он присвоен, выведя на экран все атрибуты функции Plus.
Подробней об атрибуте Protected см. книгу Е. М. Воробьёва [1, с. 142, 144–145].
Существует ещё один способ присваивания значений защищённым выражениям — применение так называемых верхних значений. Этот способ позволяют ассоциировать правила преобразований с элементами, находящимися на первом уровне выражений: при этом совершенно не важно, является ли заголовок защищённым. Присваивание осуществляется функциями UpSet и UpSetDelay, инфиксные формы которых выглядят как " ^= " и " ^:= ", соответственно.
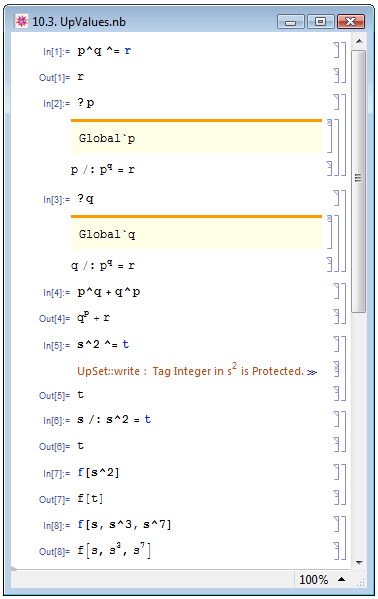
Для иллюстрации возможностей использования верхних значений приведём пример, аналогичный примеру в книге Е. М. Воробьёва [1, с. 145]. В In[1] на рис. 10.3 мы заменяем выражение p^q символом r. Теперь символ r ассоциирован с выражениями p и q и является их верхним значением, в чём мы убеждаемся в примерах In[2] и In[3], запрашивая сведения об этих выражениях. В примере In[4] на рис. 10.3 мы вводим некоторое выражение, содержащее p^q, и в результате вычислений Out[4] видим, что p^q действительно было заменено символом r.
В примере In[5] на рис. 10.3 мы попробуем присвоить верхнее значение t выражению s^2. К нашему удивлению, попытка совершить подобное действие терпит фиаско: Mathematica выдаёт сообщение о том, что защищённым является заголовок Integer, который, как мы знаем, отвечает за целочисленный тип данных. Заставить Mathematica осуществить присваивание в этом случае невозможно, поскольку правило преобразования можно ассоциировать с символами, и нельзя — с числами и строками. Однако и из этой, казалось бы, тупиковой ситуации есть выход. Можно присвоить верхнее значение выражению s^2, ассоциировав новое правило только с символом s в этом выражении. Делается это при помощи функции TagSet, инфиксная форма которой " /: " (примеры In[6] и In[7]). Поскольку в наших примерах s ассоциировано с t только в выражении s^2, то все выражения s, s^3, s^7 и т.д. останутся в прежнем виде и не будут ничем заменены (пример In[8]).
Следует отметить, что в ряде случаев в поздних версиях Mathematica на попытку выполнить выражение вроде  программа выдаёт сообщение об ошибке, но присваивание всё-таки осуществляет. Так или иначе, уповать на это не стоит, и следует пользоваться тем методом, который однозначно, без дополнительных сообщений, приводит к требуемому результату.
программа выдаёт сообщение об ошибке, но присваивание всё-таки осуществляет. Так или иначе, уповать на это не стоит, и следует пользоваться тем методом, который однозначно, без дополнительных сообщений, приводит к требуемому результату.