Уравнения. Системы уравнений
Цель лекции: познакомиться с основными возможностями, принципами и средствами Mathematica для решения алгебраических и дифференциальных уравнений, систем уравнений.
8.0. Введение
Доступ к множеству оригинальных алгоритмов при помощи встроенных функций, широчайшие возможности символьного и графического представления результатов делают Mathematica эффективным инструментом аналитического и численного решения уравнений. В данной лекции мы познакомимся с основными функциями Mathematica, применяемыми для нахождения решений алгебраических, трансцендентных и дифференциальных уравнений, а также систем уравнений. В этом нам помогут книги Е. М. Воробьёва [1] и А.Н. Прокопени [5].
8.1. Нахождение символьных решений алгебраических и трансцендентных уравнений
Наиболее часто используемая функция для решений уравнений — Solve. Она позволяет находить решения полиномиальных уравнений вплоть до чётвёртого порядка, некоторых полиномиальных уравнений высших порядков, а также неполиномииальных уравнений (А. Н. Прокопеня и А. В. Чичурин [5, с. 28]). В простейшем случае для решения одного уравнения lhs==rhs (lhs и rhs — левая и правая части уравнения, соответственно) с одной неизвестной var функция задаётся в виде Solve[lhs==rhs,var] (пример In[1] на рис. 8.1). Корни уравнения выдаются в виде вложенного списка правил замены в виде подстановок (см. Out[1])
Для того чтобы решить при помощи этой функции систему уравнений, нужно задать оба обязательных аргумента в виде списков уравнений и переменных, т. е., записать функцию как Solve[{lhs1==rhs1,lhs2==rhs2,...},{var1,var2,...}]. Уравнения также можно отделять друг от друга логическим оператором && (логическим умножением).
В примере In[2] на рис. 8.1 мы решили систему уравнений. Обратим внимание на то, в каком виде мы получаем корни системы. В Out[2] мы получаем вложенный список, элементами которого являются одномерные списки. Каждый одномерный список в качестве элементов содержит пару корней системы уравнений.
Для того чтобы была возможность в дальнейшем производить манипуляции с корнями уравнения или системы уравнений, следует от вложенного списка правил преобразований перейти к одномерному списку корней уравнения или системы уравнений. Делается это при помощи уже известного нам оператора " /. ". Так в примере In[3] на рис. 8.1 мы присвоили выражению xroots список корней системы уравнений в In[2] для переменной x.
Обратиться к конкретному корню уравнения или системы уравнений теперь можно, пользуясь навыками работы со списками. Так в примере In[4] на рис. 8.1 мы вывели на экран первое правило подстановки из списка, полученного в результате решения уравнения In[2], а в In[5] — второй в списке набор корней этого же уравнения с учётом преобразования In[3].
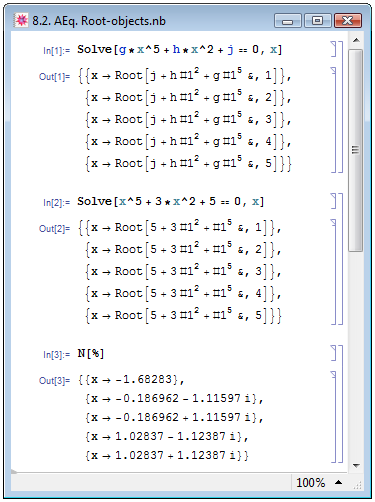
Если Mathematica не может представить решение полиномиального уравнения в аналитическом виде, например, в случае, если полином в уравнении имеет степень выше четвёртой, то корни таких уравнений представляются программой при помощи Root-объектов (А. Н. Прокопеня и А. В. Чичурин [5, с. 29]). Такой объект в виде Root[f,k] представляет точное значении корня с номером k полиномиального уравнения f[x]==0. Пример полученных в таком виде решений — Out[1] на рис. 8.2.
В примере In[1] на рис. 8.2 мы находили решение уравнения, заданного в общем виде. Если все коэффициенты уравнения имеют численные значения (как в примере In[2]), то получить численные значения корней не составляет труда при помощи функции N — пример In[3].
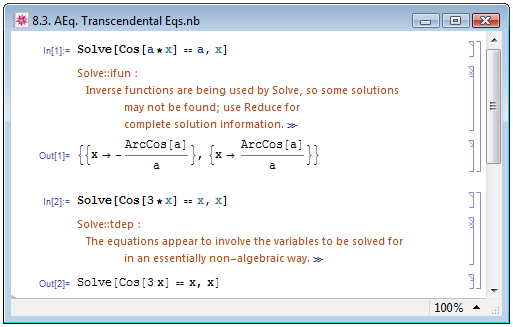
В предыдущих примерах обсуждались возможности функции Solve применительно к алгебраическим уравнениям. В примере In[1] на рис. 8.3 мы попробовали решить с её помощью трансцендентное уравнение ![Cos[a*x]==a](/sites/default/files/tex_cache/953e0492d15f978d50a0744b495ea4e6.png) относительно переменной x. Понятие трансцендентного уравнения в Mathematica ничем не отличается от его понятия в математике: Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические и др. функции.
относительно переменной x. Понятие трансцендентного уравнения в Mathematica ничем не отличается от его понятия в математике: Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические и др. функции.
Как мы видим в Out[1] на рис. 8.3, для нашего трансцендентного уравнения Mathematica также сумела найти корень. Мы знаем, что на самом деле такое уравнение имеет бесконечное число корней, отличающихся на  . Знает это и Mathematica: поэтому она выдаёт сообщение о том, что помимо найденного ей могут существовать и другие корни уравнения.
. Знает это и Mathematica: поэтому она выдаёт сообщение о том, что помимо найденного ей могут существовать и другие корни уравнения.
Однако в ряде случаев Mathematica оказывается бессильной найти корни трансцендентного уравнения в символьном виде. Тогда она выдаёт сообщение, в котором честно признаётся в своём бессилии и рекомендует попробовать решить уравнение неалгебраическими (численными) методами (см. пример In[2] на рис. 8.3).
Подробней о функции Solve и её возможностях см. книги Е. М. Воробьёва [1, с. 45–50] и А. Н. Прокопени и А. В. Чичурина [5, с. 28–29].