| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Графический метод оптимизации линейных моделей
Упражнения
Задача 1.4
В качестве упражнения предлагается решить графически следующую задачу по планированию работы зверофермы:
На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество кормов каждого вида, которое должны получать животные, приведено в таблице. В ней также указаны общее количество корма каждого вида, которое может быть использовано зверофермой ежедневно, и прибыль от реализации одной шкурки лисицы и песца. Определить, сколько лисиц и песцов можно вырастить при имеющихся запасах корма.
| Вид корма | Количество единиц корма, которое ежедневно должны получать | Запас корма | |
|---|---|---|---|
| лисица | песец | ||
 |
2 | 2 | 180 |
 |
4 | 1 | 240 |
 |
6 | 7 | 426 |
| Прибыль от реализации одной шкурки, руб. | 1600 | 1200 | |
Попробуйте найти решение самостоятельно, а затем сравните его с приведенным ниже.
Пусть  — количество лисиц, а
— количество лисиц, а  — количество песцов, которые еще можно содержать при имеющихся материальных
ресурсах.
— количество песцов, которые еще можно содержать при имеющихся материальных
ресурсах.
Построим прямоугольную систему координат, где по оси  отложим значения
отложим значения  , а по оси
, а по оси 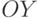 отложим значения
отложим значения
 . Значения
. Значения
 и
и  неотрицательны, поэтому можно ограничиться рассмотрением первого квадранта (рисунок 1.9).
неотрицательны, поэтому можно ограничиться рассмотрением первого квадранта (рисунок 1.9).
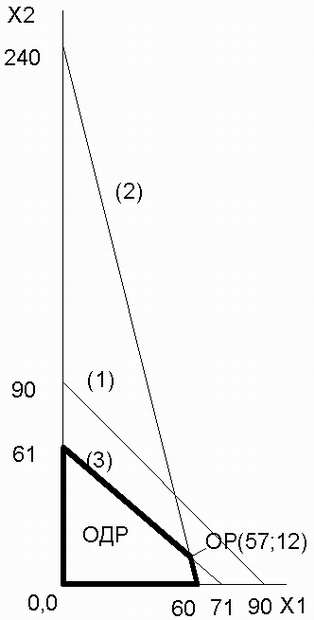
Рассмотрим последовательно все ограничения по ресурсам кормов:
 — расход корма
— расход корма  не может превышать его запасы.
не может превышать его запасы.
Заменим в данном ограничении знак неравенства знаком равенства:
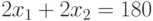 или
или
 |
( 1) |
Построим прямую (1) на графике рисунке 1.9.
Аналогично, для второго и третьего ограничений:
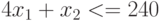 — расход корма
— расход корма  не может превышать его запасы.
не может превышать его запасы.
 — расход корма
— расход корма  не может превышать его запасы.
не может превышать его запасы.
Построим ограничительные прямые (2) и (3) по уравнениям:
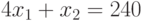 |
( 2) |
 |
( 3) |
Каждая из прямых (1), (2), (3) делит координатную плоскость на две полуплоскости. Одна полуплоскость расположена выше прямой, вторая ниже. Чтобы найти ту полуплоскость, которая соответствует неравенствам, необходимо взять любую точку, принадлежащую одной из полуплоскостей (например, точку 0,0) и подставить ее координаты в неравенство. Если неравенство будет верным, то данная полуплоскость является искомой. Область допустимых решений обведена полужирной линией. Оптимальное решение определяется координатами точки ОР: звероферме можно одновременно содержать 57 лисиц и 12 песцов.
Задача 1.5
При подкормке посевов необходимо внести на 0,01 га почвы не менее 8 единиц азота, не менее 24 единиц фосфора и не менее 16 единиц калия. Фермер закупает комбинированные удобрения двух видов "Азофоска" и "Комплекс". В таблице указаны содержание количества единиц химического вещества в 1 кг каждого вида удобрений и цена 1 кг удобрений. Определить графически потребность фермера в удобрениях того и другого вида на 0,01 га посевной площади при минимальных затратах на потребление.
| Химические вещества | Содержание химических веществ в 1 кг удобрения | |
|---|---|---|
| Азофоска | Комплекс | |
| Азот | 1 | 2 |
| Фосфор | 12 | 3 |
| Калий | 4 | 4 |
| Цена 1 кг удобрения, руб. | 50 | 20 |
Ответ: для подкормки требуется на каждые 0,01 га закупить 1,14 кг "Азофоски" и 3,43 кг удобрения "Комплекс" на сумму 125, 71 руб. Внесение удобрений будет соответствовать такому графику:
Задача 1.6
Полной даме необходимо похудеть, а за помощью она обратилась к подруге. Подруга посоветовала перейти на рациональное питание, состоящее из двух продуктов P и Q.
Суточное питание этими продуктами должно давать менее 14 единиц жира (чтобы похудеть), но не менее 300 килокалорий. На упаковке продукта Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 килокалорий, а на упаковке с продуктом Q — 4 единицы жира и 200 килокалорий соответственно. При этом цена продукта Р равна 250 руб./кг, а цена продукта Q равна 210 руб./кг.
Так как дама была стеснена в средствах, то ее интересовал вопрос: в какой пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и истратить как можно меньше денег?
Составьте ментальную карту по условиям задачи.
Решите задачу графически. Определите область допустимых решений. Найдите оптимальное решение.
Ответ: даме необходимо потреблять за сутки 0,00 кг продукта Р и 1,50 кг продукта Q, всего на сумму 315,00 руб.